Dijkstra algorithm:

Basic ideas: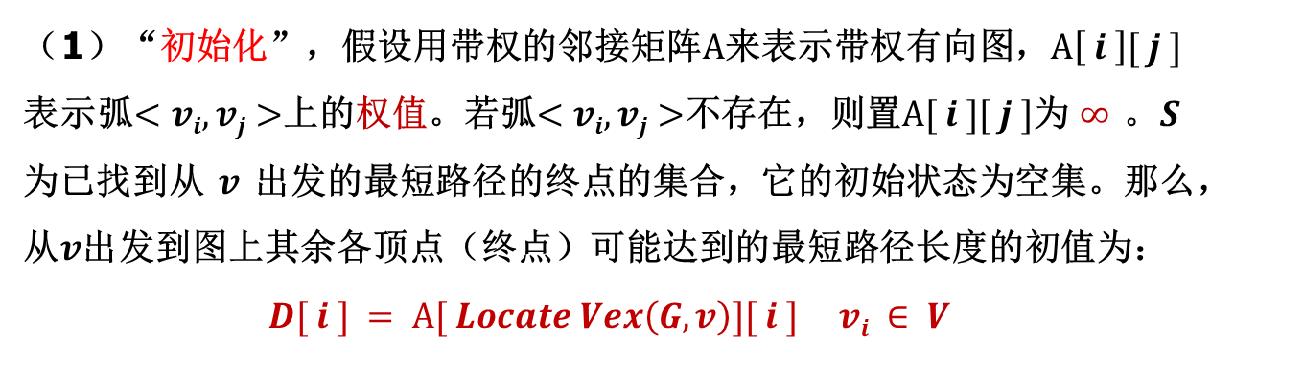




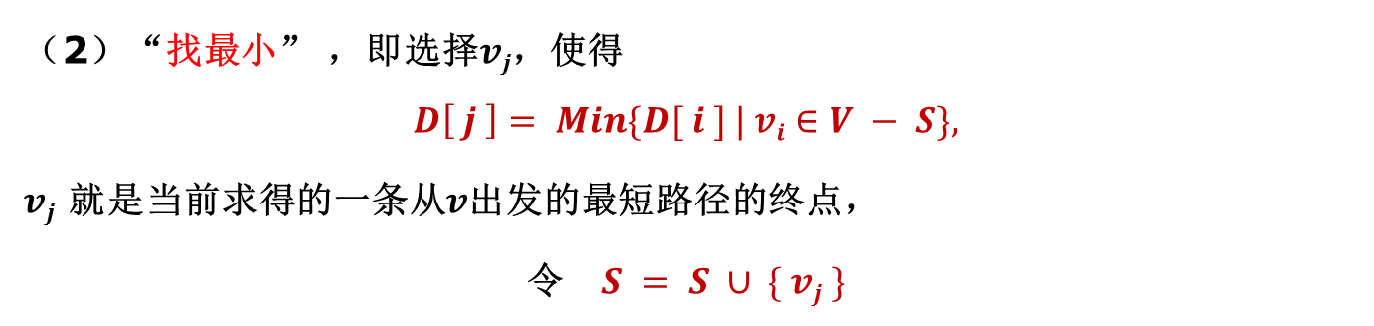
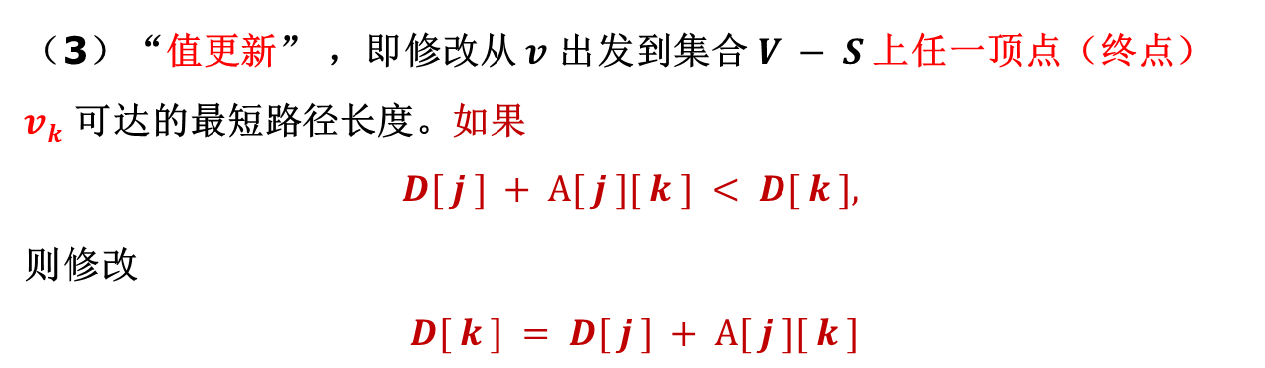
Can't understand? It doesn't matter. i will take you to understand the algorithm through specific problems

Problem Description:

Find the shortest way from business to school
Multiple sets of inputs, for each set of data.
Input N and m in the first line to indicate that there are N intersections and M roads on the street. The first intersection is the location of the business, and the nth intersection is the location of the school.
Next, row M, three integers in each row, w,v,t, means that there is an edge with weight t (T > = 0) between u and v.
The code is as follows. It's written by myself. It's absolutely easy to understand and understand. Basically, it's annotated

Specific code

#include<stdio.h>
#include <stdlib.h>
#define INF 10000 
#define MAXTIME 10
int shortestP();
int main(){
	int output[MAXTIME] = {0};
	for(int i = 0;i < MAXTIME;i++){
		int t = shortestP();
		if(t == -1)break;
		output[i] = t;
	}
	for(int i = 0;i < MAXTIME;i++){
		if(output[i]!=0)
			printf("%d\n",output[i]);
	}
	return 0;
} 
int shortestP(){
	int N = 0;int M = 0;
	scanf("%d%d",&N,&M);
	if(N==0 && M==0) return -1;
	int **arc;
	arc = (int **)malloc(sizeof(int *) * N);
	for(int i = 0 ;i < N ; i++)  
    arc[i]= (int*)malloc(sizeof(int) * N);
	
	//Initialize the value of each edge 
	for(int i = 0;i < N;i++){
		for(int y = 0;y < N;y++){
			arc[i][y] = INF;
		}		
	}
	for(int i = 0; i < M;i++){
		int w,v,t;
		scanf("%d%d",&w,&v);
		scanf("%d",&t);
		//There was a problem: the w-th element, whose angle is marked w-1 
//		arc[w][v] = t;
//		arc[v][w] = t;
		arc[w-1][v-1] = t;
		arc[v-1][w-1] = t;
	} 
	
	int distance[N];//Minimum distance from origin to all points 
	//int pass[N]; / / the sequence number of the previous node of the node. Because the output path is not required for the problem, this attribute is not required 
	bool over[N]; //Record whether the point has been listed in the shortest path, that is, whether it has been selected, and the initial value is 0
	//Initialize these values 
	for(int i = 0; i < N; i++){
		//pass[i] = 0;
		over[i] = false; 
		distance[i] =  arc[0][i];
	} 
	over[0] = true;
	
	//printf("initialization complete"); 
	//Carry out N-1 rounds of searching, find a point closest to the shortest circuit at a time and list it as the shortest circuit
	//And check whether all points are closer to the shortest circuit, and update 
	for(int i = 1; i < N;i++){
		int min = INF;//The minimum distance found in this round of searching 
		int tar = 0;//This round looks for the shortest point to be found, initially 0 
		//Traverse each point, u is the number of the inspected point 
		for(int u = 1; u < N; u++){
			//Find the minimum 
			if(!over[u] && distance[u] < min){
				min = distance[u];
				tar = u;
			}
		} 
		over[tar] = 1;
		//Update the shortest distance. After adding a new point, you only need to compare the distance through the new point with the original shortest distance 
		for(int i = 1;i < N;i++){
			if(!over[i] && distance[tar] + arc[tar][i] < distance[i]) 
				distance[i] = distance[tar] + arc[tar][i];
		} 
	} 
	//printf("establish shortest path completion");  
	//Release 2D array 
	for(int i = 0;i<N;i++){
	  free(arc[i]);
	} free(arc);
	return distance[N-1];
}