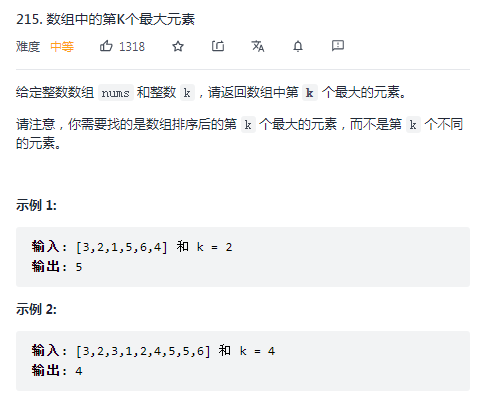
The title requires the k-largest element in the array. My most direct idea is to sort the whole array and then return the k-largest element in the array.
1. Bubble sorting
To complete the sorting of the array nums, bubble sorting requires nums.size() - 1 round of sorting, because the last element does not need to be sorted. Bubble sort each round of sorting will put the maximum value in the array to be arranged at the end of the array.
Therefore, to find the k-th largest element in the array, you only need to do K rounds of sorting.
Bubble sorting can be sorted from small to large (positive order) or from large to small (reverse order).
The following describes the implementation of positive sequence and reverse sequence respectively.
1.1 bubble sorting from small to large
If the sorting principle is from small to large, num.size () - 1 is the last element of the array and the maximum value in the array. Then the k-th element is in the nums.size() - k bit of the array.
Bubble sorting adopts double-layer cycle, the inner cycle is one-time sorting, and the outer cycle is k-time sorting. After the k-th sorting, the array index num.size () - K is the k-largest element in the array.
The time complexity of the algorithm is O(n) ²) , There is still a large optimization space, so quick sorting with low time complexity can be considered.
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
for(int last_position = nums.size() - 1; last_position >= nums.size() - k; last_position--)
{
// Set the standard bit to optimize the worst case (the whole array is in reverse order)
int flag = 0;
for(int i = 0; i < last_position; i++)
{
if(nums[i] > nums[i + 1])
{
swap(nums[i], nums[i + 1]);
flag = 1;
}
}
// If there is no element exchange after one sorting, it indicates that the array is ordered. Just exit
if(flag == 0) break;
}
// Returns the k-th largest element
return nums[nums.size() - k];
}
};
1.2 bubble sorting from large to small
If the sorting principle is from large to small, the maximum value of the array is at the first place of the array, and the array index is 0. Therefore, the index of the k-th largest element in the array is k - 1. Finally, Num [K - 1] is returned.
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
for(int last_position = nums.size() - 1; last_position >= k - 1; last_position--)
{
for(int j = 0; j < last_position; j++)
{
if(nums[j] < nums[j + 1])
{
swap(nums[j], nums[j + 1]);
}
}
}
return nums[k - 1];
}
};
2. Quick selection and sorting
Quick select sort is an upgraded version of quick sort. Quick sort needs to recursively select the array on the left of the main element and the array on the right of the main element. However, our purpose is not to sort the whole array, but to find the k-largest element in the array. Do we still need to recursively select the arrays on the left and right of the main element at the same time?
For quick sorting, the primary element will be selected first, and then the primary element will be placed in the appropriate position in the array, that is, the elements on the left of the primary element are smaller than the primary element, and the elements on the right of the primary element are larger than the primary element (sorted from small to large). Generally, the partition function is used to complete the task of placing the primary element. After calling the partition function, the primary elements will be arranged in order, and then the position will not be changed.
Using this feature, we can compare the relationship between the kth largest element in the array and the position of the principal element. Note that the kth largest element in the array refers to the position of the kth largest element after ranking.
When the two are equal, it means that the principal element is the k-largest element in the array, and the principal element can be returned directly.
When the position of the primary element is greater than the kth largest element in the array, it means that the current primary element is greater than the kth largest element in the array. Therefore, you can select another element from the array to the left of the primary element as the primary element, and judge the positional relationship between the new primary element and the kth largest element in the array.
When the position of the primary element is less than the k-th largest element in the array, it means that the current primary element is less than the k-th largest element in the array. Therefore, you can select another element from the array to the right of the primary element as the primary element, and judge the positional relationship between the new primary element and the k-th largest element in the array.
We can use recursive and non recursive methods to realize fast selection sorting, which are introduced below respectively.
2.1 quick sort optimization
Generally, we choose the first element of the array as the primary element by default.
However, if the array is arranged in reverse order, the algorithm will encounter the worst case, and the time complexity is O(n) ²).
Therefore, we need to select a more appropriate principal element, which can be selected by randomization.
int idx = left + rand() % (right - left + 1); swap(nums[idx], nums[left]); int pivot = nums[left];
idx is a number between [left,right], that is, a number in the array, but this number is randomly selected.
Each time the partition function is called, idx is selected, and then the array elements with indexes idx and left are exchanged,
And assign the array elements with the index of left to the pivot main element, so as to randomly select the array elements as the main element.
2.2 quick select sort (non recursive)
Non recursive implementation of sorting from small to large
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int left = 0;
int right = nums.size() - 1;
int n = nums.size();
while(left < right)
{
int index = partition(nums, left, right);
if(index == n - k)
{
return nums[n - k];
}
else if(index < n - k)
{
left = index + 1;
}
else if(index > n - k)
{
right = index - 1;
}
}
return nums[n - k];
}
// Put the principal element in the right place
int partition(vector<int>& nums, int left, int right)
{
int idx = left + rand() % (right - left + 1);
swap(nums[idx], nums[left]);
int pivot = nums[left];
while(left < right)
{
while(left < right && nums[right] >= pivot)
{
right--;
}
nums[left] = nums[right];
while(left < right && nums[left] <= pivot)
{
left++;
}
nums[right] = nums[left];
}
nums[left] = pivot;
return left;
}
};
Non recursive implementation of sorting from large to small
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int left = 0;
int right = nums.size() - 1;
while(left < right)
{
int index = partition(nums, left, right);
if(index == k - 1)
return nums[k - 1];
else if(index > k - 1)
{
right = index - 1;
}
else if(index < k - 1)
{
left = index + 1;
}
}
return nums[k - 1];
}
int partition(vector<int>& nums, int left, int right)
{
int idx = left + rand() % (right - left + 1);
swap(nums[idx], nums[left]);
int pivot = nums[left];
while(left < right)
{
while(left < right && nums[right] <= pivot)
{
right--;
}
nums[left] = nums[right];
while(left < right && nums[left] >= pivot)
{
left++;
}
nums[right] = nums[left];
}
nums[left] = pivot;
return left;
}
};
2.3 quick select sort (recursive)
The recursive implementation of sorting from small to large is given below.
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int n = nums.size();
quicksort(nums, 0, n - 1, k);
return nums[n - k];
}
void quicksort(vector<int>& nums, int left, int right, int k)
{
int n = nums.size();
int index = partition(nums, left, right);
if(left < right)
{
if(index == n - k)
{
return;
}
else if(index < n - k)
{
quicksort(nums, index + 1, right, k);
}
else if(index > n - k)
{
quicksort(nums, left, index - 1, k);
}
}
return;
}
int partition(vector<int>& nums, int left, int right)
{
int idx = left + rand() % (right - left + 1);
swap(nums[idx], nums[left]);
int pivot = nums[left];
while(left < right)
{
while(left < right && nums[right] >= pivot)
{
right--;
}
nums[left] = nums[right];
while(left < right && nums[left] <= pivot)
{
left++;
}
nums[right] = nums[left];
}
nums[left] = pivot;
return left;
}
};
Recursive implementation of sorting from large to small
class Solution {
public:
int findKthLargest(vector<int>& nums, int k) {
int left = 0;
int right = nums.size() - 1;
return quicksort(nums, left, right, k);
}
int quicksort(vector<int>& nums, int left, int right, int k)
{
int index = partition(nums, left, right);
if(left < right)
{
if(index == k - 1)
return nums[k - 1];
else if(index > k - 1)
return quicksort(nums, left, index - 1, k);
else if(index < k - 1)
return quicksort(nums, index + 1, right, k);
}
return nums[k - 1];
}
int partition(vector<int>& nums, int left, int right)
{
int idx = left + rand() % (right - left + 1);
swap(nums[idx], nums[left]);
int pivot = nums[left];
while(left < right)
{
while(left < right && nums[right] <= pivot)
{
right--;
}
nums[left] = nums[right];
while(left < right && nums[left] >= pivot)
{
left++;
}
nums[right] = nums[left];
}
nums[left] = pivot;
return left;
}
};