1, ID3 algorithm

1. Ladle

import numpy as np
import pandas as pd
import sklearn.tree as st
import math
import matplotlib
import os
import matplotlib.pyplot as plt

2. Read data

data = pd.read_csv('C:/Watermelon dataset.csv',header=None)
data

3. Coding

entropy

def calcEntropy(dataSet):
    mD = len(dataSet)
    dataLabelList = [x[-1] for x in dataSet]
    dataLabelSet = set(dataLabelList)
    ent = 0
    for label in dataLabelSet:
        mDv = dataLabelList.count(label)
        prop = float(mDv) / mD
        ent = ent - prop * np.math.log(prop, 2)

    return ent

Split dataset

def splitDataSet(dataSet, index, feature):
    splitedDataSet = []
    mD = len(dataSet)
    for data in dataSet:
        if(data[index] == feature):
            sliceTmp = data[:index]
            sliceTmp.extend(data[index + 1:])
            splitedDataSet.append(sliceTmp)
    return splitedDataSet

Optimal feature

def chooseBestFeature(dataSet):
    entD = calcEntropy(dataSet)
    mD = len(dataSet)
    featureNumber = len(dataSet[0]) - 1
    maxGain = -100
    maxIndex = -1
    for i in range(featureNumber):
        entDCopy = entD
        featureI = [x[i] for x in dataSet]
        featureSet = set(featureI)
        for feature in featureSet:
            splitedDataSet = splitDataSet(dataSet, i, feature)  # Split dataset
            mDv = len(splitedDataSet)
            entDCopy = entDCopy - float(mDv) / mD * calcEntropy(splitedDataSet)
        if(maxIndex == -1):
            maxGain = entDCopy
            maxIndex = i
        elif(maxGain < entDCopy):
            maxGain = entDCopy
            maxIndex = i

    return maxIndex

Find up to tags

def mainLabel(labelList):
    labelRec = labelList[0]
    maxLabelCount = -1
    labelSet = set(labelList)
    for label in labelSet:
        if(labelList.count(label) > maxLabelCount):
            maxLabelCount = labelList.count(label)
            labelRec = label
    return labelRec

tree

def createFullDecisionTree(dataSet, featureNames, featureNamesSet, labelListParent):
    labelList = [x[-1] for x in dataSet]
    if(len(dataSet) == 0):
        return mainLabel(labelListParent)
    elif(len(dataSet[0]) == 1): #There are no separable properties
        return mainLabel(labelList)  #Select the most label as the label of the dataset
    elif(labelList.count(labelList[0]) == len(labelList)): # All belong to the same Label
        return labelList[0]

    bestFeatureIndex = chooseBestFeature(dataSet)
    bestFeatureName = featureNames.pop(bestFeatureIndex)
    myTree = {bestFeatureName: {}}
    featureList = featureNamesSet.pop(bestFeatureIndex)
    featureSet = set(featureList)
    for feature in featureSet:
        featureNamesNext = featureNames[:]
        featureNamesSetNext = featureNamesSet[:][:]
        splitedDataSet = splitDataSet(dataSet, bestFeatureIndex, feature)
        myTree[bestFeatureName][feature] = createFullDecisionTree(splitedDataSet, featureNamesNext, featureNamesSetNext, labelList)
    return myTree

Drawing

def readWatermelonDataSet():
    dataSet = data.values.tolist()
    featureNames =['color and lustre', 'Root', 'Knock', 'texture', 'Umbilicus', 'Tactile sensation']
    #Get featureNamesSet
    featureNamesSet = []
    for i in range(len(dataSet[0]) - 1):
        col = [x[i] for x in dataSet]
        colSet = set(col)
        featureNamesSet.append(list(colSet))
    
    return dataSet, featureNames, featureNamesSet


matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']


decisionNode = dict(boxstyle="sawtooth", fc="0.8")


leafNode = dict(boxstyle="round4", fc="0.8")


arrow_args = dict(arrowstyle="<-")


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def getNumLeafs(myTree):
    numLeafs = 0

    firstStr = list(myTree.keys())[0]

    secondDict = myTree[firstStr]

    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    maxDepth = 0

    firstStr = list(myTree.keys())[0]

    secondDic = myTree[firstStr]

    for key in secondDic.keys():
        if type(secondDic[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDic[key])

        else:
            thisDepth = 1

        if thisDepth > maxDepth:
            maxDepth = thisDepth

    return maxDepth


def plotMidText(cntrPt, parentPt, txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
   
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
   
    createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
    
    numLeafs = getNumLeafs(myTree=myTree)

    
    depth = getTreeDepth(myTree=myTree)

    
    firstStr = list(myTree.keys())[0]

    
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)

    
    plotMidText(cntrPt, parentPt, nodeTxt)

    
    plotNode(firstStr, cntrPt, parentPt, decisionNode)

    
    secondDict = myTree[firstStr]

   
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD

   
    for key in secondDict.keys():
       
        if isinstance(secondDict[key], dict):
            plotTree(secondDict[key], cntrPt, str(key))
        else:
           
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
           
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))

   
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD


def createPlot(inTree):
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW
    plotTree.yOff = 1.0
    plotTree(inTree, (0.5, 1.0), '')
    plt.show()

dataSet, featureNames, featureNamesSet=readWatermelonDataSet()
testTree= createFullDecisionTree(dataSet, featureNames, featureNamesSet,featureNames)
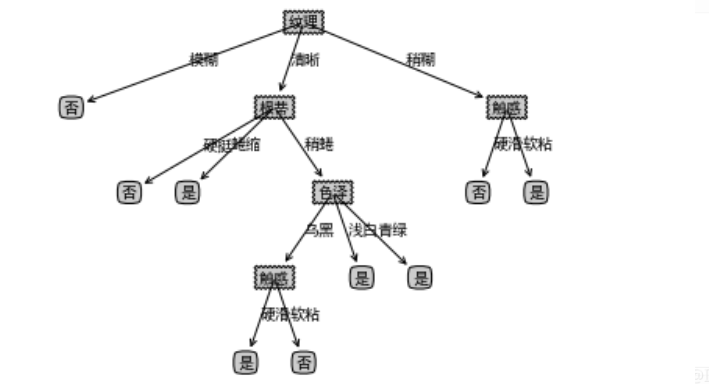
createPlot(testTree)

result

2, Implementation of sklearn ID3 and CART algorithm

1.ID3

import pandas as pd
from sklearn.preprocessing import LabelEncoder
from sklearn.tree import DecisionTreeClassifier

data = pd.read_csv('C:/Watermelon dataset.csv',header=None)
data

label = LabelEncoder()    

for col in data[data.columns[:-1]]:
    data[col] = label.fit_transform(data[col])
data

# Fit with ID3
dtc = DecisionTreeClassifier(criterion='entropy')
# Fit
dtc.fit(data.iloc[:,:-1].values.tolist(),data.iloc[:,-1].values) 
# Tag corresponding code
result = dtc.predict([[0,0,0,0,0,0]])
#Fitting results
result

2.CART

# Fit with CART
dtc = DecisionTreeClassifier()
# Fit
dtc.fit(data.iloc[:,:-1].values.tolist(),data.iloc[:,-1].values) 
# Tag corresponding code
result = dtc.predict([[0,0,0,1,0,0]])
#Fitting results
result

3, Summary

1.ID3 algorithm

By calculating the information gain of each attribute, ID3 algorithm considers that the attribute with high information gain is a good attribute. Each division selects the attribute with the highest information gain as the division standard, and repeats this process until a decision tree that can perfectly classify training samples is generated.
Decision tree is used to classify data to achieve the purpose of prediction. The decision tree method first forms a decision tree according to the training set data. If the tree can not give correct classification to all objects, select some exceptions to the training set data and repeat the process until a correct decision set is formed. Decision tree represents the tree structure of decision set.
The decision tree consists of decision nodes, branches and leaves. The top node in the decision tree is the root node, and each branch is a new decision node or a leaf of the tree. Each decision node represents a problem or decision, which usually corresponds to the attributes of the object to be classified. Each leaf node represents a possible classification result. In the process of traversing from top to bottom along the decision tree, a test will be encountered at each node. Different test outputs of problems on each node will lead to different branches, and finally reach a leaf node. This process is the process of classification using the decision tree and using several variables to judge the category.

2.CART algorithm

(1) Select an independent variable, and then select a value to divide the dimensional space into two parts. All points of one part are satisfied, and all points of the other part are satisfied. For discontinuous variables, there are only two values of attribute value, that is, equal to or not equal to the value.

(2) Recursive processing, re select an attribute from the above two parts according to step (1) and continue to divide until the whole dimensional space is divided.