1. Overview

The core of this course is the concept of the network - the network is a mode of interrelationship between things. For example, the social network we are in reflects the social connection between friends. wait.

1.1 basic problems of network

Let's start with the network structure in several societies

The presentation and annotation of loan networks among financial institutions reveal different parts and their functions.

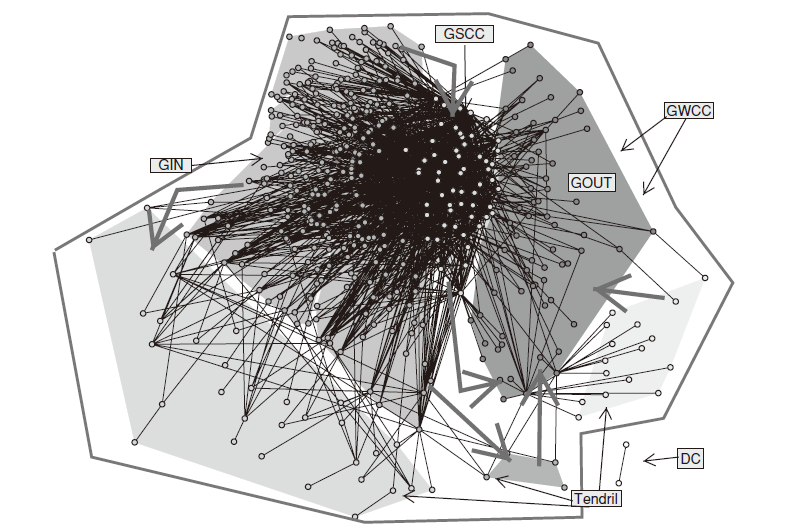
The network structure of political blog before 2004 US presidential election

Behavior and dynamics

When people talk about the connectivity of complex systems, they are actually talking about two related issues - connectivity at the structural level (who is connected with whom); connectivity at the behavioral level (each individual's actions have implicit consequences for each other in the system)
Changes in the amount of Youtube queries on Google over time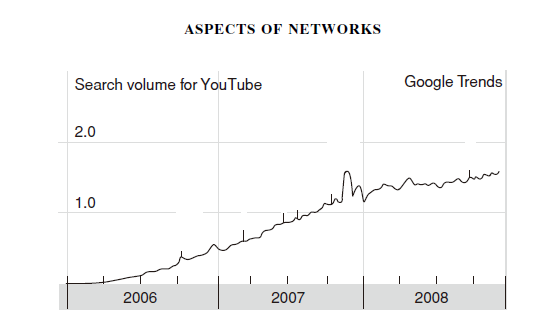

The visibility of this increase is the aggregation effect of the whole crowd behavior. To understand how these processes work, and how they are implemented by many people's interconnected behaviors, we need to study the dynamics of aggregation behavior.

The interweaving of multidisciplinary thoughts

Will use the idea of mathematical modeling, modeling is a very important idea, is the process of converting practical problems into mathematical problems. "Knowledge that cannot be described in mathematical language cannot be called science, and practical problems that cannot be modeled cannot be considered as practical solutions." (bragging from someone) it's important anyway.
One of the central objectives of this book is to combine research practices in various fields to help form such a synthesis.

1.2 core content of the book

Two main theories are graph theory and game theory.
Needless to say, people who have not studied graph theory cannot be called computer learners.
Game theory is the feature of this book - game theory provides a model of individual behavior, the point is that the result of individual behavior depends on the behavior of other individuals.

2. Experiment

2.1 calculation of aggregation coefficient and neighborhood overlap

requirement

Input: adjacency matrix of any graph
Output:
1) Aggregation factor per node
2) Neighborhood overlap of each node pair

Related definitions

1) Ternary closure: in a social circle, if two people have a common friend, the possibility of these two people becoming friends in the future will increase.
2) Aggregation coefficient: the aggregation coefficient of node a is defined as the probability that any two friends of node a are friends with each other - that is, the ratio of the actual number of edges between adjacent nodes of node A / the number of pairs of adjacent nodes of node a
The aggregation coefficient a) is 1 / 6 B) is 1 / 2 in the figure below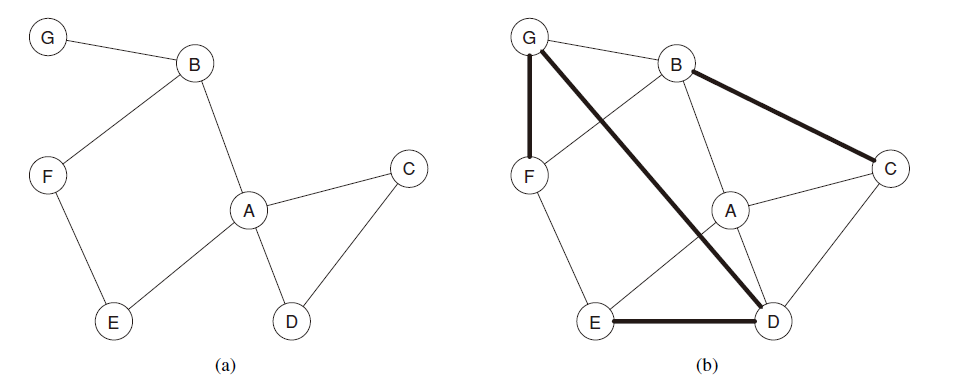

3) Bridge and local bridge: Bridge refers to the only path between two endpoints, as shown in the figure below, the edge between A and B is the bridge.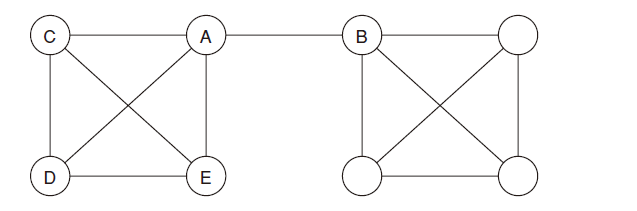

Shortcut: if endpoint A and B of edge AB have no common friends, then edge AB is called shortcut. As shown below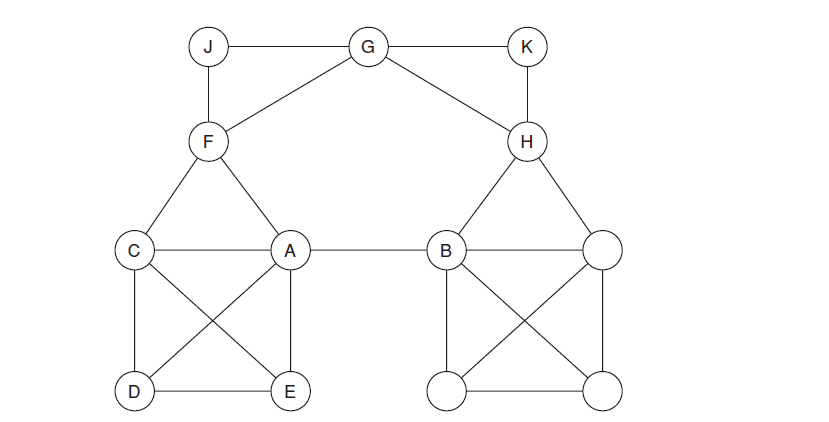

Relationship: it is obvious from the figure that the bridge must be a shortcut, but the shortcut is not necessarily a bridge
4) Strong ternary closure property: all relationships in social networks are divided into two types: strong connection (friend) and weak connection (acquaintance). If the relationship between node A and node B and C is strong, and there is no connection (strong or weak) between node B and C, then node a violates the strong ternary closure property. Otherwise, node a satisfies the strong ternary closure property
All points in the following graph satisfy the strong ternary closure property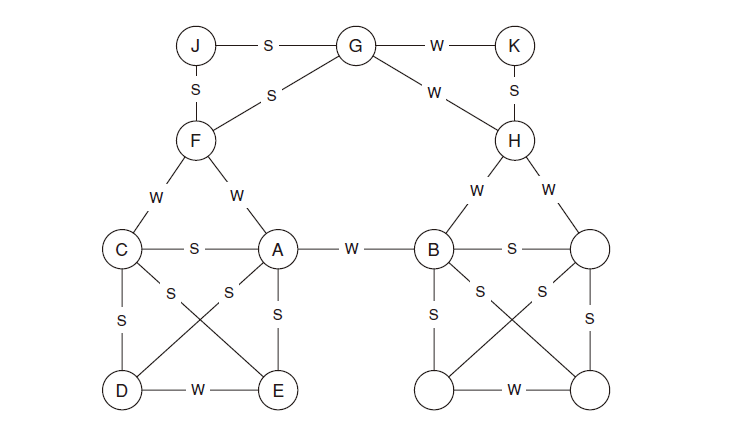

5) Shortcut and weak connection: in social networks, if node A satisfies the strong ternary closure property and has at least two strong connection edges connected with it, then any shortcut connected with it is weak connection
The proof is as follows: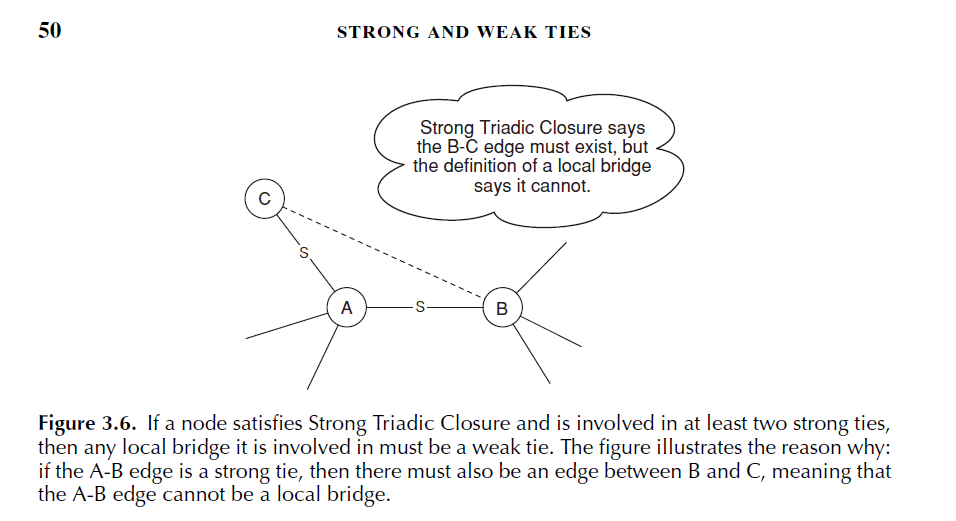

6) Neighborhood overlap degree: defines the neighborhood overlap degree of an edge as: the number of nodes with A and B as neighbors / the number of nodes with A and B as neighbors (excluding A and B)
It can be seen that when the molecule is zero, that is, the neighborhood overlap is zero, this side is a shortcut

Algorithm and code

Algorithm: 1) calculate the aggregation coefficient: first, calculate the number of possible connections between all nodes connected with the current node (calculation method: (degree (degree-1) / 2) (using the sequence of equal difference numbers), which will be used as the denominator, and then calculate how many nodes are actually connected, which will be used as the numerator. 2) Find neighborhood overlap: define the ratio of "node number of neighbors with A and B" and "node number of neighbors with at least one of A and B" of (A, B) edge
The input is as follows:

Graph structure (use adjacency matrix to store graph structure. The UML class diagrams of the three main classes are as follows):

Main code:
graph

template <class T>
class graph{
public:
  virtual ~graph(){};

  virtual int numberOfVertices() const = 0;
  virtual int numberOfEdges() const = 0;
  virtual bool existsEdge(int ,int ) const = 0;
  virtual void insertEdge(edge<T>* ) = 0;//edge is a template class

  virtual void easeEdge(int ,int ) = 0;
  virtual int degree(int) const = 0;
  virtual int inDegree(int ) const = 0;
  virtual int outDegree(int ) const = 0;

  virtual bool directed() const = 0;
  virtual bool weighted() const = 0;

  //Access adjacent vertices s of specified vertices
  virtual vertexIterator<T>* iterators(int ) = 0;

};

adjacencyWDigraph

template <class T>
class adjacencyWDigraph : public graph<T>{
protected:

  int n;
  int e;


  T noEdge;//Indicates an edge that does not exist

public:

  T **a;//adjacency matrix 

  //1. Constructor with default parameters
  adjacencyWDigraph(int nV = 0,T theNoEdge =0){
      if(nV < 0){
          throw "Number of vertices must be greater than 0!";
      }

      n = nV;
      e = 0;
      noEdge = theNoEdge;
      //make2dArray(a,n+1,n+1);
      //Create adjacency matrix

      a = new T*[n+1];//The array of arrays is a two-dimensional array

      for (int j = 1; j <=n  ; ++j) {
          a[j] = new T[n+1];
      }

      for (int i = 1; i <= n ; ++i) {
          //Initialize adjacency matrix
          for (int j = 1; j <=n ; ++j) {
              a[i][j] = noEdge;
          }
      }

  }




  int numberOfVertices() const { return n;}
  int numberOfEdges() const { return e;}
  bool directed() const { return true;}
  bool weighted() const { return true;}

  //2. Judge whether (i, j) edge exists
  bool existsEdge(int i,int j) const{
      if (i<1||j<1||i>n||j>n||a[i][j] == noEdge){
          return false;
      } else{
          return true;
      }
  }

  //3. Insert edge
  void insertEdge(edge<T>* theEdge){

      int v1 = theEdge->vertex1();
      int v2 = theEdge->vertex2();

      if(v1<1||v2<1||v1>n||v2>n||v1==v2){
          throw "This insertion is illegal!";
      } else{
          if (a[v1][v2] == noEdge){
              e++;
          }
          a[v1][v2] = theEdge->weight();
      }

  }

  //4. Delete edge
  void easeEdge(int i,int j){
      if(existsEdge(i,j)){
          a[i][j] = noEdge;
          e--;
      }
  }

  //5. Degree of vertex
  int degree(int theV) const{
      throw "Directed graph has the difference between in degree and out degree!";
  }

  //6. In and out
  int outDegree(int theV) const {

      int sum = 0;
      for (int i = 1; i <= n; ++i) {
          if (a[theV][i] != noEdge){
              sum++;
          }
      }

      return sum ;
  }
  int inDegree(int theV) const{
      int sum = 0;

      for (int i = 1; i <= n ; ++i) {
          if(a[i][theV] != noEdge){
              sum++;
          }
      }
      return sum;
  }

  //7. Ergodic class
  class myIterator : public vertexIterator<T>{
  public:
      myIterator(T* theRow,T theNoEdge,int numberOfV){
          row = theRow;
          noEdge = theNoEdge;
          n = numberOfV;
          currentVertex = 1;
      }

      ~myIterator(){}

      int next(T & theWeight){
          for (int i = currentVertex; i <= n ; ++i) {
              if (row[i] != noEdge){
                  currentVertex = i+1;
                  theWeight = row[i];
                  return i;
              }
          }

          //There is no next adjacent vertex
          currentVertex = n+1;
          return 0;

      }

      int next(){
          for (int i = currentVertex; i <= n ; ++i) {
              if (row[i] != noEdge){
                  currentVertex = i+1;
                  return i;
              }
          }
          //There is no next adjacent vertex
          currentVertex = n+1;
          return 0;

      }

  protected:
      T* row;
      T noEdge;
      int n;
      int currentVertex;
  };

  myIterator* iterators(int theV){
      return new myIterator(a[theV],noEdge,n);
  }



};

adjacencyWGraph

template<class T>
class adjacencyWGraph : public adjacencyWDigraph<T> {
public:
  adjacencyWGraph(int numberOfVertices = 0, T theNoEdge = 0)
          : adjacencyWDigraph<T>(numberOfVertices, theNoEdge) {}

  void insertEdge(int v1, int v2, int weight) {
      if (v1 < 1 || v2 < 1 || v1 > this->n || v2 > this->n || v1 == v2) {
          throw "Illegal insertion!";
      }

      //Insert if edge does not exist
      if (this->a[v1][v2] == this->noEdge)
          this->e++;

      this->a[v1][v2] = weight;
      this->a[v2][v1] = weight;
  }

  bool directed() const { return false; }

  void eraseEdge(int i, int j) {
      if (i >= 1 && j >= 1 && i <= this->n && j <= this->n && this->a[i][j] != this->noEdge) {
          this->a[i][j] = this->noEdge;
          this->a[j][i] = this->noEdge;
          this->e--;
      }
  }

  int degree(int theVertex) const {
      int sum = 0;
      for (int j = 1; j <= this->n; j++)
          if (this->a[theVertex][j] != this->noEdge)
              sum++;

      return sum;
  }

  int outDegree(int theVertex) const {
      return degree(theVertex);
  }

  int inDegree(int theVertex) const {
      return degree(theVertex);
  }


//Any two friends returned to A are also friends
  int getFriendsIsFriends(int iE) {

      int *friends = new int[degree(iE)];
      int start = 0;
      for (int j = 1; j <= this->n; ++j) {
          if (this->existsEdge(iE, j)) {
              friends[start++] = j;
//Cout < < adjacent vertices are: < J < < endl;
          }
      }

      int friendsIsFriends = 0;
      //Check whether friends are friends
      for (int i = 0; i < degree(iE); i++) {
          //Check the value of this line
          for (int k = 0; k < degree(iE) - 1 - i; k++) {

              int a = friends[i];
              int b = friends[i + 1 + k];
              if (this->existsEdge(a, b)) {
                  friendsIsFriends++;
              }
          }
      }
      return friendsIsFriends;

  }

//Returns the vertex adjacent to vertex i
  int *getEdges(int i) {
      int *my_result = new int[this->degree(i)];
//Cout < < I < < the degree is: < this - > degree (I) < endl;
      int start = 0;
      for (int j = 1; j <= this->n ; ++j) {
          if (this->existsEdge(i,j)){
              my_result[start++] = j;
//                The critical points of cout < I < are < J < endl;
          }
      }
//Several adjacent points of cout < < I < < are: < sizeof (my_ Result) < endl; / / returns the size of the pointer
      return my_result;
  }
};

Find the aggregation coefficient

string aggCoeff[n+1];//Record the aggregation coefficient of each vertex
    for (int k = 1; k <= n; ++k) {
        int my_degree = 0;

        my_degree = graph.degree(k);
//Cout < < degree is < < My_ degree<<endl;cout<<endl;
        int denominator = my_degree*(my_degree-1)/2;
        if (denominator==0){
            aggCoeff[k]="0";
        } else{
            int molecule = graph.getFriendsIsFriends(k);
//Cout < < molecular is: < molecular < < endl;
            if(molecule==0){
                aggCoeff[k]="0";
            } else{
                int temp=molecule/denominator;
                if(temp==1){
                    aggCoeff[k]="1";
                } else{
                    aggCoeff[k]=to_string(molecule)+"/"+to_string(denominator);
                }
            }
        }
    }
    for (int l = 1; l <= n; ++l) {
        cout<<"vertex"<<l<<"The aggregation coefficient of is:"<<aggCoeff[l]<<endl;
    }

Find the aggregation coefficient between neighbors

//Record the neighborhood overlap of each pair of adjacent nodes
    string *degreeEdges = new string[e];
    int start2 = 0;
    for (int m = 1; m < n ; ++m) {
        for (int i = m+1; i <=n ; ++i) {
            if (graph.existsEdge(m,i)){
                //Obtain the vertex adjacent to A and B
                int *getAEdges = graph.getEdges(m);
                int *getBEdges = graph.getEdges(i);

                int legA = graph.degree(m);
                int legB = graph.degree(i);

                if(legA==1&&legB==1){
                    degreeEdges[start2++]="0";
                } else{
                    int denominator = getDeno(getAEdges,getBEdges,legA,legB);
                    int molecule = getCoin(getAEdges,getBEdges,legA,legB);

                    if(denominator==molecule){
                        degreeEdges[start2++]="1";
                    } else if(molecule==0){
                        degreeEdges[start2++]="0";
                    } else{
                        degreeEdges[start2++]=to_string(molecule)+"/"+to_string(denominator);
                    }
                }

                cout<<"Side("<<m<<","<<i<<")The degree of neighborhood overlap between them is:"<<degreeEdges[start2-1]<<endl;

            }
        }
    }

2.2 Schelling model simulation

requirement

Input: matrix of n*n, two nodes of random layout
Output:
1) Output corresponding results after adjusting parameters
2) Need interface display

Related definitions

1) Homogeneity: we and our friends tend to have the same characteristics, that is, as the proverb goes, "birds of a feather flock together, and people flock together."
2) Choice and social influence: Choice - people choose friends with more similar characteristics, which is a subjective behavior. Social impact - people change their behavior because they need to be consistent with their friends, which is an objective impact.
3) Community: the focus of social interaction.
4) Affiliation Networks: indicates the individual's affiliation to the community. It's a bipartite graph.

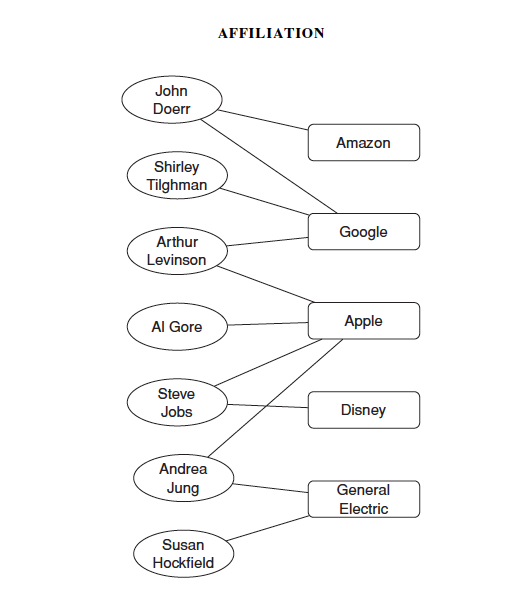
5) Social affiliation network: it includes not only the social networks among individuals, but also the affiliation networks between individuals and communities.

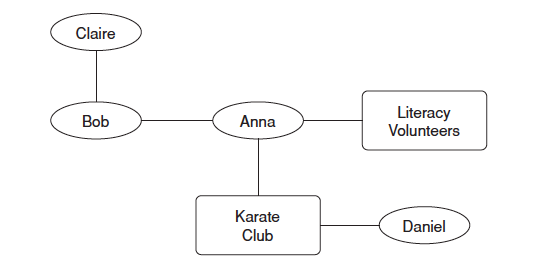
The principle of ternary closure has a new development in social belonging network

6) Social closure: two individuals tend to establish a connection because they participate in the same community.

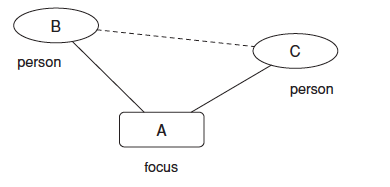
7) membership closure: individual B will tend to join the community in which friend A participates.

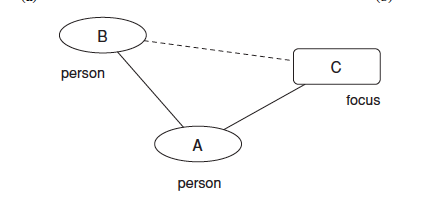
We can see that community closure is a subjective choice and membership closure is an objective social impact.

8) Schelling model: describes the effect of homogeneity on spatial isolation. (Chinatown and ghettos in the United States are examples of Schelling's model. )

Algorithm and code

1) Thought:
The basic constraint of this model is that each agent must be a neighbor with a certain number of similar agents. We assume that the threshold value t is applicable to all agents: if an agent finds that he has fewer neighbors than t, he is interested in moving to other units. We call such agents dissatisfied with the status quo. For example, figure (a) is a kind of annotation of figure (b). Unsatisfactory agents use "*" to indicate that the corresponding threshold value is equal to 3. We also add a number after each agent, which is equivalent to giving each agent a name. However, the key here is to distinguish whether the agent belongs to a thousand X type or an O type.

Figure (b)

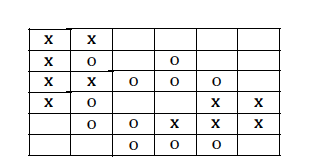
Figure (a)

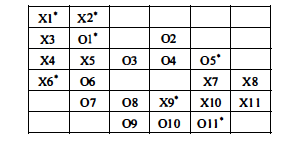
2) Algorithm: gradually detect whether each pixel is lower than the threshold value, if lower than the threshold value, move.

3) Key code:

%Calculate the number of pixels according to the percentage
empty_tmp = round(m * empty / 100); 
ratio_tmp = round((m - empty_tmp) * ratio / 100);
sim_tmp = sim / 100;
str_tmp = get(handles.round_text,'String'); %obtain ROUND NUMBER String of
not_satis_red=[]; %Initialization dissatisfied red dot sequence
not_satis_blue=[];%Not satisfied with the initialization of blue dot sequence
empty_now=[];%Initializing a sequence of blank pixels
%R(i,j)=1 For empty, 2 for red dot, 3 for blue dot
for i=1:size
  for j=1:size
      switch R(i,j)
          case 1
              empty_now = [empty_now (j-1)*size+i];
          case 2
              satis_tmp = 0;
              amount_tmp = 0;
              %Unsatisfied detection    
              if i ~= 1 && R(i-1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= 1 && R(i,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= size && R(i,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && R(i+1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && R(i-1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= 1 && R(i,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= size && R(i,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && R(i+1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if satis_tmp<round(sim_tmp*amount_tmp)
                  not_satis_red =[not_satis_red (j-1)*size+i];
              end
          case 3
              satis_tmp = 0;
              amount_tmp = 0;
              if i ~= 1 && R(i-1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= 1 && R(i,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if j ~= size && R(i,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && R(i+1,j) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) == R(i,j) satis_tmp = satis_tmp + 1; end
              if i ~= 1 && j ~= 1 && R(i-1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && R(i-1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= 1 && j ~= size && R(i-1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= 1 && R(i,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if j ~= size && R(i,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= 1 && R(i+1,j-1) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && R(i+1,j) ~= 1 amount_tmp = amount_tmp + 1; end
              if i ~= size && j ~= size && R(i+1,j+1) ~= 1 amount_tmp = amount_tmp + 1; end
              if satis_tmp<round(sim_tmp*amount_tmp)
                  not_satis_blue =[not_satis_blue (j-1)*size+i];
              end
      end
  end
end

GitHub source code