What is a balanced binary tree?

For binary search tree, different insertion order of nodes will lead to different depth and search efficiency. So there's a problem. How to design the structure of binary tree to make the search more efficient? If a tree has the same left and right subtrees. Both the height of the left and right subtrees and the number of nodes are the same, so the search efficiency is the highest, but the same requirements are too high. If we lower the standard a little bit, we will have a balanced binary tree.
Balance factor: BF (T) = HL HR, where HL and HR respectively represent the height of left and right subtrees of the number t.
Balanced binary tree (AVL tree): the absolute value of height difference of empty tree, or left subtree and right subtree does not exceed 1, i.e., < BF (T) < 1.
Adjustment of balanced binary tree:
After inserting or deleting a node, the balanced binary tree may lose its balance. According to different actual situations,

We divide the adjustment of binary tree into the following methods:

RR rotation:
physical truth: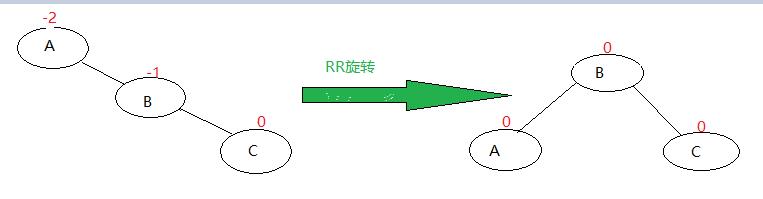

As shown in the figure, after inserting node C into the tree on the left, the balance factor of node A becomes - 2. At this time, we call the "discoverer" of imbalance as node A, and the destroyer of balance, i.e. the troublesome node is node C, which is on the right subtree of the right child of node A of "discoverer". In this case, we use RR rotation to get the tree on the right. (RR rotation is also called right single rotation)
All troublesome nodes in the right subtree of the discoverer's right child need (RR rotation) can be summarized as follows: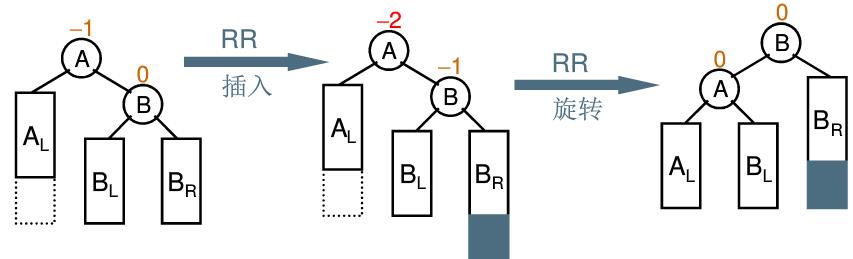

LL rotation: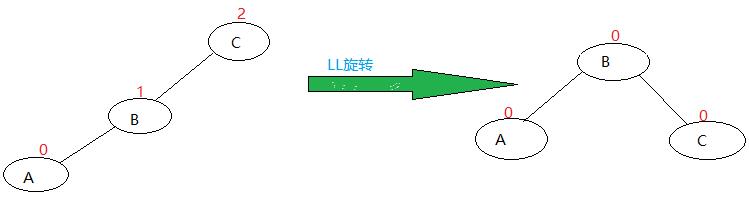

As shown in the figure: the left tree breaks the balance of node C after inserting node A. Trouble node A, on the left subtree of the left child of discoverer node C
In this case, we use LL rotation to get the tree on the right. (LL rotation is also called left single rotation)
The situation that all troublesome nodes need (LL rotation) on the left subtree of the discoverer's left child can be summarized as follows:

LR rotation: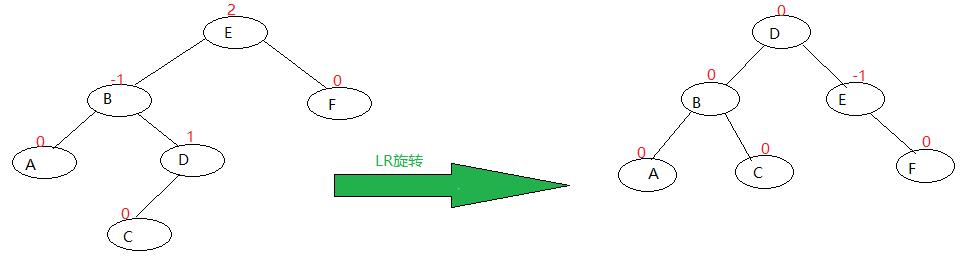

As shown in the figure: the left tree breaks the balance of E nodes after inserting node C. Trouble node C, on the right subtree of the left child of discoverer node E
In this case, we use LR rotation to get the tree on the right. (LR rotation is also called LR double rotation, because in the above figure, it is formed by taking the left child B of discoverer node E as the root node, making a right single rotation, and then taking E as the root node and making a left single rotation.)
The situation that all trouble nodes need (LR rotation) on the right subtree of the left child of the discoverer can be summarized as follows:

RL rotation: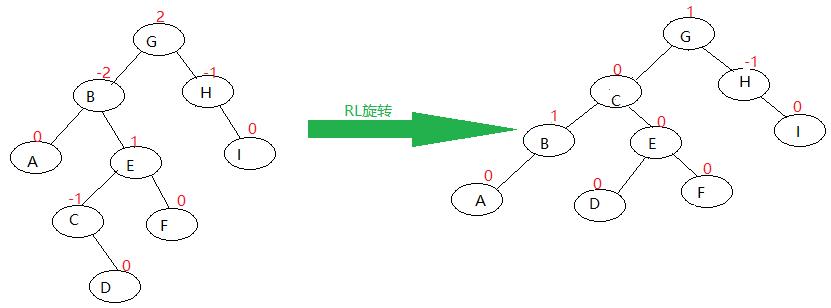

As shown in the figure: the left tree breaks the balance of node B after inserting node D. Trouble node D, on the left subtree of the right child of discoverer node B
In this case, we rotate RL to get the tree on the right. (RL rotation, also known as RL double rotation, is similar to LR double selection)
The situation that all trouble nodes need (RL rotation) on the right subtree of the left child of the discoverer can be summarized as follows: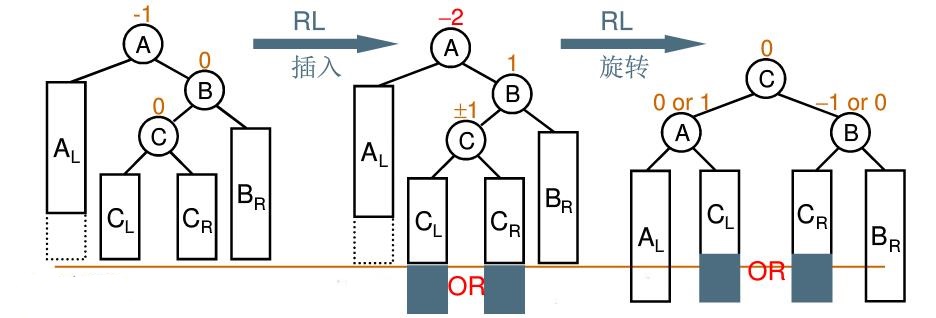

The realization of balanced binary tree adjustment:

#include<stdio.h>
#include<stdlib.h>
#define Elementype char
typedef struct AVLTree{//Structure of AVL tree
	Elementype data;
	struct AVLTree* L_child;
	struct AVLTree* R_child;
	int Hight;//Height of tree
}AVLTree;
int Max ( int a, int b )
{
    return a > b ? a : b;
}
int GetHight(AVLTree* A){//Get the height of the tree
	if(!A){
		return -1;
	}else{
		return A ->Hight;
	}
}
AVLTree* SingleLeftRotation ( AVLTree* A ){//LL rotation (left single rotation)
	// Note: A must have A left subknot
	// Rotate A and B to the left, update the height of A and B, and return to the new root node B     
	
	AVLTree* B = A ->L_child;
	A ->L_child = B ->R_child;
	B ->R_child = A;
	A ->Hight = Max(GetHight(A ->L_child) ,GetHight(A ->R_child)) + 1;
	B ->Hight = A ->Hight + 1;
	return B;
}
AVLTree* SinglRightRotation ( AVLTree* A ){//RR rotation (right single rotation)
	// Note: A must have A right child
	// Turn A and B to the right, update the height of A and B, and return to the new root node B     
	
	AVLTree* B = A ->R_child;
	A ->R_child = B ->L_child;
	B ->L_child = A;
	A ->Hight = Max(GetHight(A ->L_child) ,GetHight(A ->R_child)) + 1;
	B ->Hight = A ->Hight + 1;
	return B;
}
AVLTree* LeftRightRotation ( AVLTree* A ){//LR rotation (first RR rotation with A - > L "child, then LL rotation with A as root node)
	// Note: A must have A left child (b), B must have A right child (C)
	
	AVLTree* B = A ->L_child;
	A ->L_child = SinglRightRotation(B);
	return SingleLeftRotation(A);
}
AVLTree* RightLeftRotation ( AVLTree* A ){//RL rotation (first make LL rotation with A - > R ﹣ child, and then make RR rotation with A as the root node)
	// Note: A must have A right child (b), B must have A left child (C)
	
	AVLTree* B = A ->R_child;
	A ->R_child = SingleLeftRotation(B);
	return SinglRightRotation(A);
}
AVLTree* Insert(  AVLTree* A , Elementype data ){//Insert operation of balance tree
	if(!A){
		A = (AVLTree*)malloc(sizeof(AVLTree));
		A ->data = data;
		A ->Hight = 0;
		A ->L_child = A ->R_child = NULL;
	}else if(data < A ->data){//data should be inserted into the left subtree of A
		A ->L_child = Insert( A ->L_child , data);
		if(GetHight( A ->L_child ) - GetHight( A ->R_child) == 2){//Imbalance after insertion
			if(data < A ->L_child ->data){//LL rotation
				A = SingleLeftRotation(A);
			}else{//LR rotation
				A = LeftRightRotation(A);
			}
		}
	}else if(data > A ->data){// data should be inserted into the right subtree of A
		A ->R_child = Insert(A ->R_child , data);
		if( GetHight( A ->L_child ) - GetHight( A ->R_child ) == -2 ){
			if( data > A ->R_child ->data ){//RR rotation
				A = SinglRightRotation(A);
			}else{//RL rotation
				A = RightLeftRotation(A);
			}
		}
	}
	//Update tree height
	A ->Hight = Max( GetHight( A ->L_child) , GetHight( A ->R_child )) + 1;
	return A;
}
void Pre_show_Tree(AVLTree* ptr){//First order traversal output AVL tree
	if(ptr){
		printf("%c ",ptr ->data);
		Pre_show_Tree(ptr ->L_child);
		Pre_show_Tree(ptr ->R_child);
	}
}