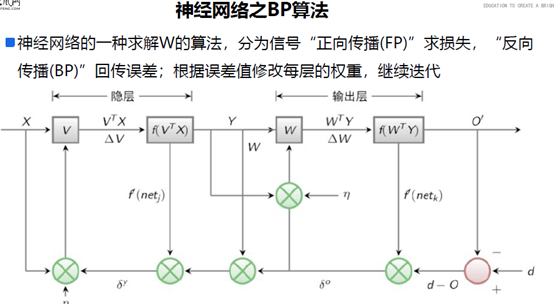
BP algorithm is also called delta algorithm

It's a way to solve parameters

Case study;

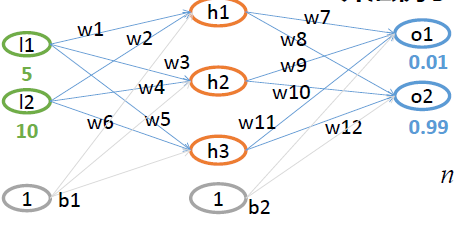
Required input (5, 10), output (0.01, 0.99)

Hypothesis: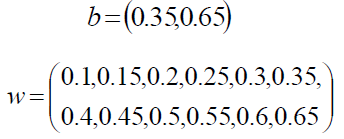

Calculate the output of h1:

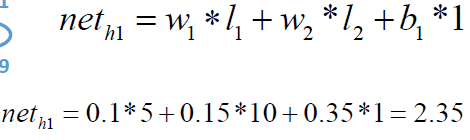
In the same way:

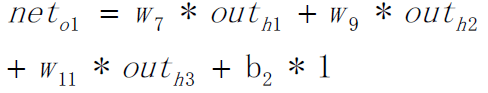
Calculate the output of o1, o2:

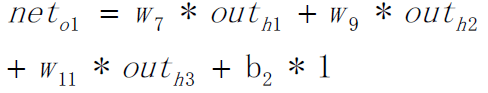
Calculated output error:

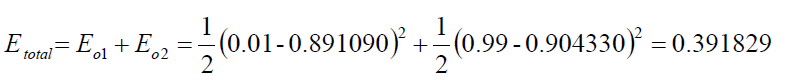
Calculation: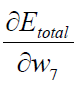

Known: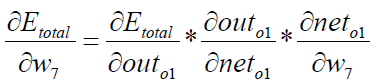

Among them:

(，)

()

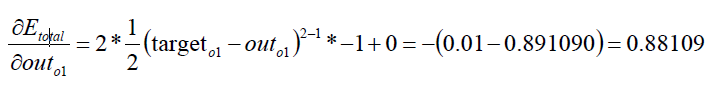
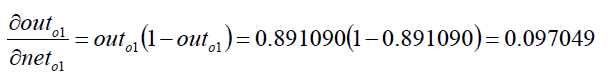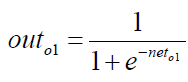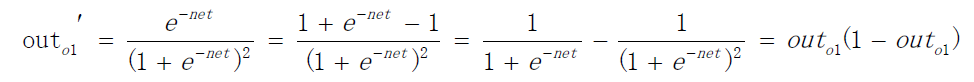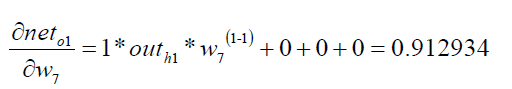
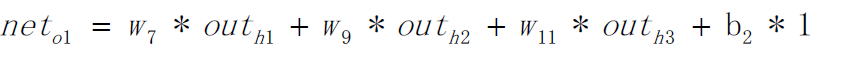So: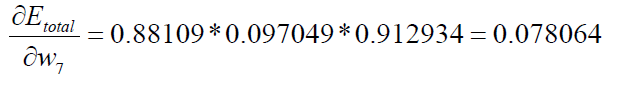

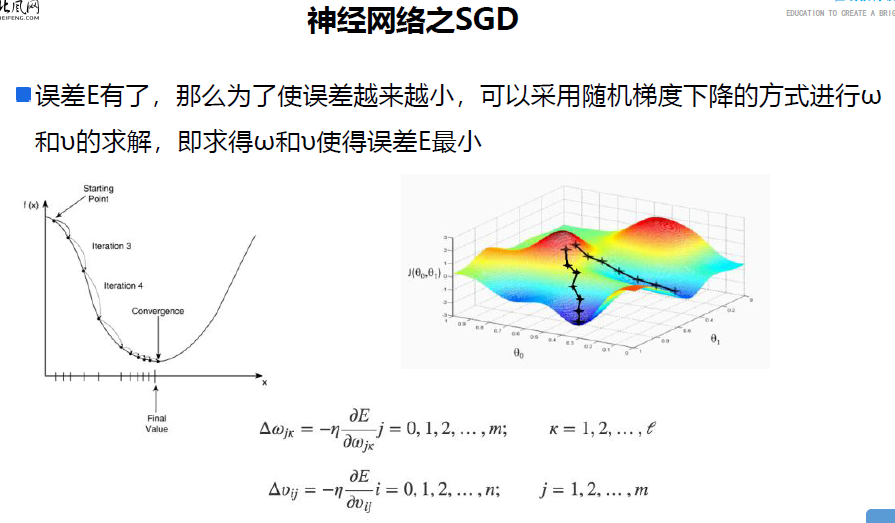
In fact, it can be summarized as follows:

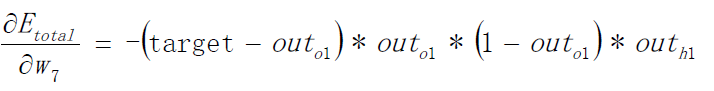
Finally:

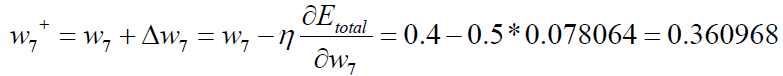
In the same way: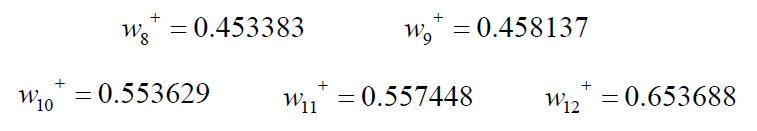

Next, we need to ask: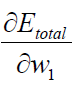

Known:

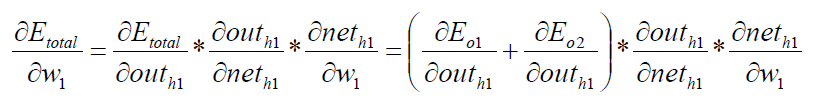
Among them:

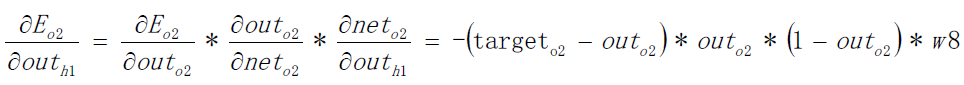
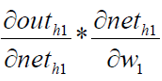The solution of is similar to the previous one.

Finally, we get: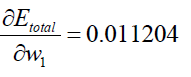

So: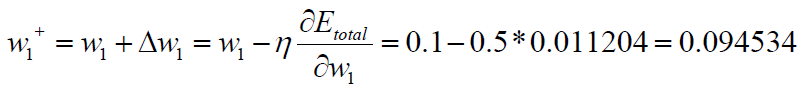

In the same way:

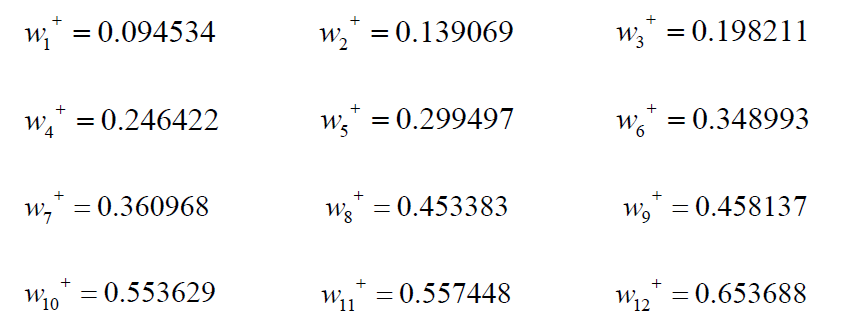
b1 and b2 remain unchanged:

How to modify b?

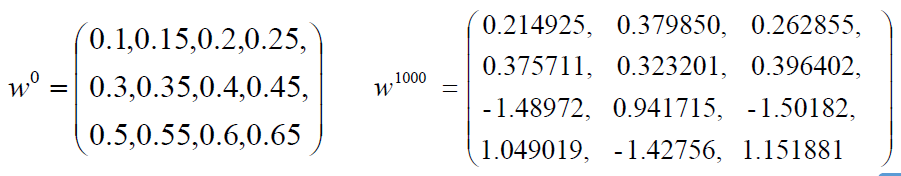
code:

# -- encoding:utf-8 --
"""
Create by ibf on 2018/5/6
"""

import numpy as np
w=[0.1,0.15,0.2,0.25,0.3,0.35,0.4,0.45,0.5,0.55,0.6,0.65]
b=[0.35,0.65]
l=[5,10]

def sigmoid(z):
    return 1.0/(1+np.exp(-z))
def f1(w,b,l):
    #Forward propagation
    h1 = sigmoid(w[0]*l[0]+w[1]*l[1]+b[0])
    h2 = sigmoid(w[2] * l[0] + w[3] * l[1] + b[0])
    h3 = sigmoid(w[4] * l[0] + w[5] * l[1] + b[0])
    o1=sigmoid(w[6]*h1+w[8]*h2+w[10]*h3+b[1])
    o2 = sigmoid(w[7] * h1 + w[9] * h2 + w[11] * h3 + b[1])
    #Backward propagation
    t1=-(0.01-o1)*o1*(1-o1)
    t2 = -(0.99 - o2) * o2 * (1 - o2)
    w[6]=w[6]-0.5*(t1+h1)
    w[8] = w[8] - 0.5 * (t1 * h2)
    w[10] = w[6] - 0.5 * (t1 * h3)
    w[7] = w[7] - 0.5 * (t2 * h1)
    w[9] = w[9] - 0.5 * (t2 * h2)
    w[11] = w[11] - 0.5 * (t2 * h3)

    w[0]=w[0]-0.5*(t1*w[6]+t2*w[7])*h1*(1-h1)*l[0]
    w[1] = w[1] - 0.5 * (t1 * w[6] + t2 * w[7]) * h1 * (1 - h1) * l[1]
    w[2] = w[2] - 0.5 * (t1 * w[8] + t2 * w[9]) * h1 * (1 - h2) * l[0]
    w[3] = w[3] - 0.5 * (t1 * w[8] + t2 * w[9]) * h1 * (1 - h2) * l[1]
    w[4] = w[4] - 0.5 * (t1 * w[10] + t2 * w[11]) * h1 * (1 - h3) * l[0]
    w[5] = w[5] - 0.5 * (t1 * w[10] + t2 * w[11]) * h1 * (1 - h3) * l[1]

    return o1,o2,w


for i in range(10001):
    r1,r2,w=f1(w,b,l)
    print('{}:({},{}),{}'.format(i,r1,r2,w))

RBF

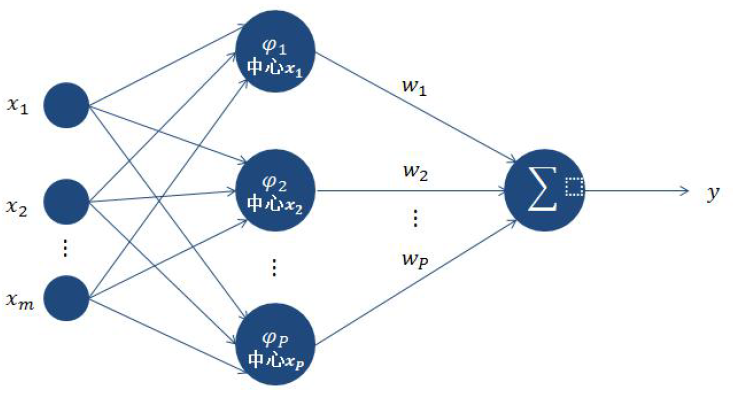
After DNN appears, RBF will not be used