Title Description

For example, give a network diagram, its source point and sink point, each edge has known its maximum flow and unit flow cost, and find out its maximum flow and minimum cost in the case of maximum flow.

I / O format

Input format:

 

The first row contains four positive integers N, M, S, and T, which respectively represent the number of points, the number of directed edges, the source point serial number, and the sink point serial number.

Next, each row of row M contains four positive integers ui, vi, WI and fi, indicating that the i-th directed edge starts from ui and arrives at vi, the edge weight is wi (that is, the maximum traffic on this side is WI), and the cost per unit traffic is fi.

 

Output format:

 

A line containing two integers, the maximum flow and the minimum cost in the case of the maximum flow.

 

Example of input and output

Input example ා 1: copy

4 5 4 3
4 2 30 2
4 3 20 3
2 3 20 1
2 1 30 9
1 3 40 5

Output example: copy

50 280

Explain

Space time limit: 1000ms,128M

(BYX: last two points changed to 1200ms)

Data size:

For 30% data: n < = 10, m < = 10

For 70% of data: n < = 1000, m < = 1000

For 100% data: n < = 5000, m < = 50000

Example description:

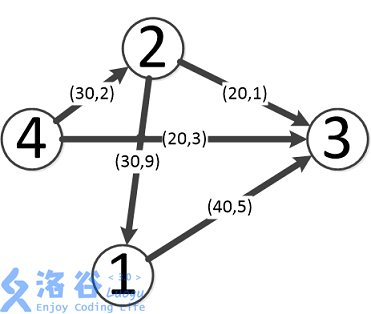
As shown in the figure, the optimal scheme is as follows:

The first flow is 4 -- > 3, the flow is 20, and the cost is 3 * 20 = 60.

The second flow is 4 -- > 2 -- > 3, the flow is 20, and the cost is (2 + 1) * 20 = 60.

The third flow is 4 -- > 2 -- > 1 -- > 3, the flow is 10, and the cost is (2 + 9 + 5) * 10 = 160.

Therefore, the maximum flow is 50, and the minimum cost under this condition is 60 + 60 + 160 = 280.

So output 50 280.

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>
//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 200005
#define inf 0x3f3f3f3f
#define INF 999999999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const int mod = 10000007;
#define Mod 20100403
#define sq(x) (x)*(x)
#define eps 1e-5
typedef pair<int, int> pii;
#define pi acos(-1.0)
const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)
inline int rd() {
    int x = 0;
    char c = getchar();
    bool f = false;
    while (!isdigit(c)) {
        if (c == '-') f = true;
        c = getchar();
    }
    while (isdigit(c)) {
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }
    return f ? -x : x;
}

ll gcd(ll a, ll b) {
    return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

bool vis[maxn];
int n, m, s, t;
int x, y, f, z;
int dis[maxn], pre[maxn], last[maxn], flow[maxn];
int maxflow, mincost;

struct node {
    int to, nxt, flow, dis;
}edge[maxn<<2];

int head[maxn], cnt;
queue<int>q;

void addedge(int from, int to, int flow, int dis) {
    edge[++cnt].to = to; edge[cnt].flow = flow; edge[cnt].dis = dis;
    edge[cnt].nxt = head[from]; head[from] = cnt;
}

bool spfa(int s, int t) {
    memset(dis, 0x7f, sizeof(dis)); memset(flow, 0x7f, sizeof(flow));
    ms(vis);
    q.push(s); vis[s] = 1; dis[s] = 0; pre[t] = -1;
    while (!q.empty()) {
        int now = q.front(); q.pop(); vis[now] = 0;
        for (int i = head[now]; i != -1; i = edge[i].nxt) {
            if (edge[i].flow > 0 && dis[edge[i].to] > dis[now] + edge[i].dis) {
                dis[edge[i].to] = edge[i].dis + dis[now];
                pre[edge[i].to] = now; last[edge[i].to] = i;
                flow[edge[i].to] = min(flow[now], edge[i].flow);
                if (!vis[edge[i].to]) {
                    vis[edge[i].to] = 1; q.push(edge[i].to);
                }
            }
        }
    }
    return pre[t] != -1;
}

void mincost_maxflow() {
    while (spfa(s, t)) {
        int now = t;
        maxflow += flow[t]; mincost += flow[t] * dis[t];
        while (now != s) {
            edge[last[now]].flow -= flow[t];
            edge[last[now] ^ 1].flow += flow[t];
            now = pre[now];
        }
    }
}

int main()
{
    //ios::sync_with_stdio(false);
    memset(head, -1, sizeof(head)); cnt = 1;
    rdint(n); rdint(m); rdint(s); rdint(t);
    for (int i = 1; i <= m; i++) {
        rdint(x); rdint(y); rdint(z); rdint(f);
        addedge(x, y, z, f); addedge(y, x, 0, -f);
    }
    mincost_maxflow();
    cout << maxflow << ' ' << mincost << endl;
    return 0;
}