KNN overview

K-nearest neighbor algorithm is a basic classification and regression method. We only discuss k-nearest neighbor algorithm in classification.

A word summary: near Zhu is red, near Mo is black! Working principle: there is a sample data set, also known as a training sample set, and each data in the sample set has a label, that is, we know the corresponding relationship between each data in the sample set and its classification. After inputting the new data without label, each feature of the new data is compared with the corresponding feature of the data in the sample set, and then the algorithm extracts the classification label of the most similar data (nearest neighbor) of the sample. Generally speaking, we only select the first k most similar data in the sample data set, which is the origin of K in the k-nearest neighbor algorithm. Generally, K is an integer no more than 20. Finally, the most frequent classification of K most similar data is selected as the classification of new data.

The input of the k nearest neighbor algorithm is the feature vector of the instance, corresponding to the point of the feature space; the output is the category of the instance, which can take more than one category. The k-nearest-neighbor algorithm assumes that given a training data set, the instance category has been determined. In classification, the new instances are predicted by majority vote according to the categories of k nearest neighbor training instances. Therefore, k-nearest neighbor algorithm does not have an explicit learning process. In fact, k-nearest neighbor algorithm uses the training data set to divide the feature vector space, and as the "model" of its classification. The selection of K value, distance measurement and classification decision rules are the three basic elements of k-nearest neighbor algorithm.

KNN scene

Movies can be classified by subject matter, so how to distinguish action movies and love movies?

1. Action movies: more fights
2. Romance: more kisses

Based on the number of kisses and fights in the movie, the theme type of the movie can be automatically divided by using the k-nearest neighbor algorithm to construct the program.

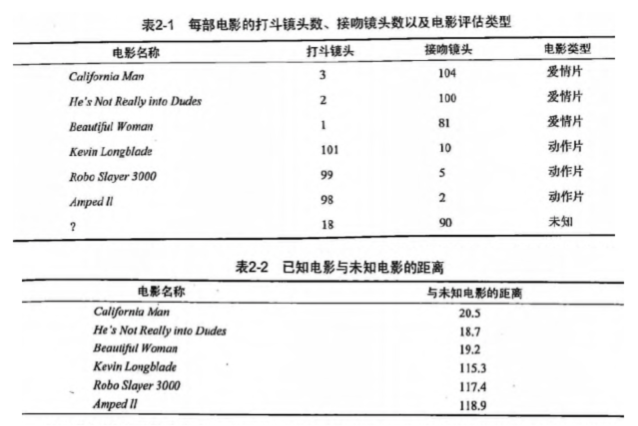
Now, according to the distance between all the films in the sample set we obtained above and the unknown films, k films with the closest distance can be found in ascending order of distance.
Assuming k=3, the three closest movies are He's Not Really into Dudes, Beautiful Woman and California Man.
knn algorithm determines the type of unknown films according to the type of the three closest films, and all of them are love films, so we determine that the unknown films are love films.
For those students who haven't figured out the concept of K-nearest-neighbor algorithm, you can look down until you have seen the whole demo, and you can understand what KNN algorithm does

KNN principle

1. Suppose there is a labeled sample data set (training sample set), which contains the corresponding relationship between each data and its classification.
2. After entering new data without labels, each feature of the new data is compared with the corresponding feature of the data in the sample set.
   1. Calculate the distance between the new data and each data in the sample data set.
   2. All the distances are sorted (from small to large, smaller means more similar).
   3. Take the classification labels corresponding to the first k (k is generally less than or equal to 20) sample data.
3. Find the most frequent classification labels in k data as the classification of new data.

Given a training data set, for a new input instance, the k instances closest to the instance are found in the training data set. Most of the k instances belong to a class, so the input instance is divided into this class.

Data collection: any method
 Prepare data: the value required for distance calculation, preferably in a structured data format
 Analysis data: any method
 Training algorithm: this step is not applicable to k-nearest neighbor algorithm
 Test algorithm: calculate error rate
 Using algorithm: input sample data and structured output results, then run k-nearest neighbor algorithm to determine which classification the input data belongs to, and finally perform subsequent processing on the calculated classification

Advantages: high precision, insensitive to outliers, no data input assumption
 Disadvantages: high computational complexity and space complexity
 Applicable data range: numerical type and nominal type

#!/usr/bin/env python
# -*- encoding: utf-8 -*-
'''
@File    :   KNN.py
@Time    :   2019/03/27 11:07:01
@Author  :   xiao ming 
@Version :   1.0
@Contact :   xiaoming3526@gmail.com
@Desc    :   KNN Nearest neighbor algorithm
@github  :   https://github.com/aimi-cn/AILearners
@reference:  https://github.com/apachecn/AiLearning
'''

# here put the import lib
from __future__ import print_function
from numpy import *
import numpy as np
import operator
# Import scientific calculation package numpy and operator module operator
from os import listdir
from collections import Counter

def createDataSet():
    """
    //Create datasets and labels
    //Calling mode
    import kNN
    group, labels = kNN.createDataSet()
    """
    group =  array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group, labels

def test1():
    group, labels = createDataSet()
    '''
    [[1.  1.1]  #Label corresponding to A
    [1.  1. ]   #Label corresponding to A
    [0.  0. ]   #Label corresponding to B
    [0.  0.1]]  #Label corresponding to B

    ['A', 'A', 'B', 'B']
    '''
    #print(str(group))
    #print(str(labels))
    #print(classify0([0.1, 0.1], group, labels, 3))
    print(classify1([0.1, 0.1], group, labels, 3))

def classify0(inX, dataSet, labels, K):
    '''
    inX: Test data for input vector input for classification
    dataSet: Input training samples
    lables: Label vector
    k: The number of nearest neighbors selected is usually less than 20
    //Note: the number of labels elements is the same as the number of dataSet rows; the program uses the Euclidean distance formula

    //For the classification of forecast data, enter the following command
    kNN.classify0([0,0], group, labels, 3)
    '''
    # -----------The first way to implement the classify0() method----------------------------------------------------------------------------------------------------------------------------
    # 1. Distance calculation
    #Calculate data size
    dataSetSize = dataSet.shape[0]
    '''
    tile Use: Column 3 indicates the number of copied rows, row 1／2 Express right inX Number of repetitions of
    In [2]: inx = [1,2,3]
    In [3]: tile(inx,(3,1))  #Column 3 represents the number of copied rows row 1 represents the number of times the inX is repeated
    Out[3]: 
    array([[1, 2, 3],
        [1, 2, 3],
        [1, 2, 3]])

    In [4]: tile(inx,(3,2)) #Column 3 represents the number of copied rows row 2 represents the number of times the inX is repeated
    Out[4]: 
    array([[1, 2, 3, 1, 2, 3],
        [1, 2, 3, 1, 2, 3],
        [1, 2, 3, 1, 2, 3]])
    '''
    # tile generates the matrix corresponding to the training sample and calculates the difference with the training sample
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet
    '''
    //Euclidean distance: distance between points
       //First line: the distance from the same point to the first point of the dataSet.
       //Second line: the distance from the same point to the second point of the dataSet.
       ...
       //Line N: the distance from the same point to the nth point of the dataSet.
    [[1,2,3],[1,2,3]]-[[1,2,3],[1,2,0]]
    (A1-A2)^2+(B1-B2)^2+(c1-c2)^2
    '''
    # Take square
    sqDiffMat = diffMat ** 2
    # Add every line of matrix
    sqDistances = sqDiffMat.sum(axis=1)
    # Square root
    distances = sqDistances ** 0.5
    #print ('distances=', distances)
    #distances= [1.3453624  1.27279221 0.14142136 0.1]
    # Sort from the smallest to the largest according to the distance, and return the corresponding index position
    sortedDistIndicies = distances.argsort()
    #print ('distances.argsort()=', sortedDistIndicies)
    #distances.argsort()= [3 2 1 0]

    # 2. Select K points with the minimum distance
    classCount = {}
    for i in range(K):
        #Find the type of the sample
        voteIlabel = labels[sortedDistIndicies[i]]
        # Add one to the type in the dictionary
        # get method of dictionary
        # For example: list.get(k,d), where get is equivalent to an if...else... Statement, if the parameter k is in the dictionary, the dictionary will return list[k]; if the parameter k is not in the dictionary, then it will return the parameter D, if the parameter k is in the dictionary, then it will return the value value corresponding to K
        # l = {5:2,3:4}
        # The value returned by print l.get(3,0) is 4;
        # The return value of Print l.get (1,0) is 0;
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    #print(classCount)
    #{'A': 1, 'B': 2}

    # 3. Sort and return the most frequent data type
    # The items() method of the dictionary returns a list of traversable (key, value) tuples.
    # For example: dict = {'name': 'Zara', 'age': 7} print "value:% s"% dict.items() value: [('age ', 7), ('name', 'Zara')]
    # The second parameter key=operator.itemgetter(1) in sorted means to compare the first few elements
    # For example: a = [('b ', 2), ('a', 1), ('c ', 0)] B = sorted (a, key = operator. Itemgetter (1)) > > b = [('c', 0), ('a ', 1), ('b', 2)] you can see that the sorting is based on the following 0,1,2, not a,b,c
    # B = sorted (a, key = operator. Itemgetter (0)) > > b = [('a ', 1), ('b', 2), ('c ', 0)] this time, it is a,b,c in front instead of 0, 1, 2
    # B = sorted (a, key = optertator. Itemgetter (1,0)) > > b = [('c ', 0), ('a', 1), ('b ', 2)] this is to compare the second element first, and then sort the first element to form a multi-level sorting.
    #We need the most frequent one now, so use reverse=True list to reverse sort
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

def classify1(inX, dataSet, labels, K):
    '''
    inX: Test data for input vector input for classification
    dataSet: Input training samples
    lables: Label vector
    k: The number of nearest neighbors selected is usually less than 20
    //Note: the number of labels elements is the same as the number of dataSet rows; the program uses the Euclidean distance formula

    //For the classification of forecast data, enter the following command
    kNN.classify0([0,0], group, labels, 3)
    '''
    # -----------The second way to implement the classify0() method----------------------------------------------------------------------------------------------------------------------------
    # Euclidean distance: distance between points
    #    First line: the distance from the same point to the first point of the dataSet.
    #    Second line: the distance from the same point to the second point of the dataSet.
    #    ...
    #    Line N: the distance from the same point to the nth point of the dataSet.

    # [[1,2,3],[1,2,3]]-[[1,2,3],[1,2,0]]
    # (A1-A2)^2+(B1-B2)^2+(c1-c2)^2
    
    # inx - dataset uses numpy broadcasting, see https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html
    # See https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.sum.html for the use of np.sum() function
    # """
    dist = np.sum((inX - dataSet)**2, axis=1)**0.5
    
    # """
    # 2. k recent Tags
    
    # Use for distance sorting numpy Medium argsort Functions, see https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.sort.html#numpy.sort
    # The function returns an index, so [0: k] is used for the first k indexes
    # Store these k labels in the list
    # """
    k_labels = [labels[index] for index in dist.argsort()[0 : K]]
	# """
    # 3. The label with the most times is the final category
    
    # Use collections.Counter to count the number of times each label appears. Most common returns the label tuple with the most times, for example [('lable1', 2)], so [0] [0] can take out the label value
	# """
    label = Counter(k_labels).most_common(1)[0][0]
    return label

if __name__ == '__main__':
    test1()
    

Input:
	dataSet: input training samples
	[[1.0,1.1] × label corresponding to A
    [1.0,1.0] × label corresponding to A
    [0, 0] × label corresponding to B
    [0, 0.1]] (label corresponding to B)

	Labels: label vector
    ['A', 'A', 'B', 'B']
    
    inX: test data for input vector input for classification
    [0.1, 0.1]
Output:
	B
 Indicates that the label of this output is closer to B input class B
###
See code Notes for details

Like to pay attention, your attention is my greatest support for writing