Hello, guys. Today, I'd like to briefly talk about the TSP problem of this repeatable city. The so-called repeatable means that the city and route can be taken casually, as long as the sum of its paths is the smallest in the end.
The knowledge points to be used are state compression dp and Floyd algorithm
1, Floyd algorithm
Floyd algorithm: floyd algorithm learning video
This little sister will take you through the whole process of floyd algorithm by hand. I believe you will have a feeling of enlightenment after reading it
The main function of floyd algorithm is to get a two-dimensional array of distance and path
1.distance[][]
Example: distance[i][j] represents the shortest distance from point I to point j
With this array, we are finished in the first step
2.path[][]
Example: path[i][j] indicates what point passes between point I and point j
public void floyd(Double[][] distance,int[][] path,Double[][] edge) {
int n = edge.length;//The edge array is an adjacency matrix
//Initialize the distance array passed in
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
path[i][j] = -1;
if (i!=j) {
distance[i][j] = edge[i][j];
}else {
distance[i][j] = 0.0;
}
}
}
//Core algorithm
for (int k=0;k<n;k++) {
for (int i=0;i<n;i++) {
for (int j=0;j<n;j++) {
if (distance[i][j]>distance[i][k]+distance[k][j]) {
distance[i][j] = distance[i][k]+distance[k][j];
path[i][j] = k;//Array of record paths
}
}
}
}
}
By calling the function jointPath(...), we can find the complete path of V0 = > V, which is also very important for us to find the path of TSP
//int[][] path: obtained from floyd
//v0: start, v: end
//idx[0]: because I want to remember the effective length of the p array, I use idx[0] to ensure that it can be used as a pointer
//ps: I have a la carte. It's not very good
public void jointPath(int[][] path,int v0,int v,int[] p,int[] idx) {
getPath(path,v0,v,p,idx);
p[idx[0]++] = v;
}
//Use paper to simulate this recursive function, and you will understand it
public void getPath(int[][] path,int v0,int v,int[] p,int[] idx) {
if (path[v0][v]==-1) {
p[idx[0]++] = v0;
return;
}
getPath(path,v0,path[v0][v],p,idx);//left
getPath(path,path[v0][v],v,p,idx);//right
}
After writing my blog, I will record a video. At station b, you can pay attention to me and see my video explanation: Leaves in the wind (my account name)
2, State compression dp
Video learning connection, just 33 minutes before watching
In this video, he will teach you the concept of dp and how to use and, or, non and XOR
The teacher spoke in great detail and explained the following topics: Shortest Hamilton ian path
This problem is similar to the problem we want to solve. If you can solve the above problem, I believe you can master it quickly.
Welcome back. I'm sure you know something about dp
Next, we should have such a thinking: that is, we only pay attention to the shortest distance from point i to point J, that is, we put our heart on the distance [] [] array. We don't need to concern what points i and j pass through, so we add i and j to dp set, so we don't care what points i and j contain 1. We won't add them to dp set, and we only care about the shortest distance, Because points and edges can be repeated
You should have got my point
Next, I'll tell you the specific idea of this problem:
First, we open an array of DP [1 < < n] [n]
Because we want to represent the state of each set, and the state has 0 ~ 111... 111(2^n-1)
When we succeed in getting our state to 111... 111(2^n-1) is the moment of our victory
Next, I'll talk about the code (read my comments carefully)
dp[s][i] = Math.min(dp[s][i],dp[s^(1<<i)][j]+distance[j][i]);// It's just crucial. The function of this thing is if the vertex i has not been added to the set (we have actually added it), will the distance from the existing vertex J as the pedal to I be shorter than the original distance
Then, I still want to talk to you
ps: the following starts from bit 0
- S & (1 < < i) example: if s: 1101 (binary), i = 2 (binary), 1 < < i = 100 (binary), then 1101 & 0100 = 0100, then we can determine whether the ith bit of S (binary) is 0 or 1 by judging that S & (1 < < i) is not equal to 0
- For the example of S ^ (1 < < i), if s: 1101 (binary), i = 2 (binary), 1 < < i = 100 (binary), then 1101 ^ 0100 = 1001 (we can change the ith bit of S (binary) to 0)
//==================State compression DP
Double[][] dp = new Double[1<<n][n];//Open array
//Initialize dp array
for (int i = 0; i < 1<<n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = Double.MAX_VALUE;
}
}
dp[1][0] = 0.0;//Put point 0 into the collection. 0: indicates that you are currently staying at point 0
for (int s=1;s<(1<<n);s++) {//1~11..11(2^n-1[1<<n])
for (int i=0;i<n;i++) {
if ((s&(1<<i))!=0) {//Vertex i is added to the set
for (int j = 0; j < n; j++) {
if ((s&(1<<j))!=0&&i!=j) {
dp[s][i] = Math.min(dp[s][i],dp[s^(1<<i)][j]+distance[j][i]);
}
}
}
}
}
Double ans = Double.MAX_VALUE;//Initialize it
//Finally, we add all the points to the set, so we can make a big announcement when we return to the origin from the last point. The shortest distance from one point to another is still obtained from distance [] []
//It is also here that I came up with the way to find the path
for (int i=1;i<n;i++) {//0 is the starting point, so don't join it
if (ans > dp[(1<<n)-1][i]+distance[i][0]) {
ans = dp[(1<<n)-1][i]+distance[i][0];
}
}
return n==1?0:ans;//Robustness
It is necessary to state the following:
@Autowired
private FloydUtil floydUtil; (this is because I used it to write the springboot project. You can see the function name and know what I'm farting. Just hug.)
- public void TSP_can_repeat_path(Double[][] dp,Double[][] dis,int[] path,int end,int n)
- public void completePath(int[][] path,int[] p,int[] initP,int[] idx)
ps: see my annotation for the specific meaning of the parameter
- Let me first talk about the function of my first algorithm. The existing state s is to continuously retreat from state T, and then find the shortest path from state t to state s to determine the point (repeat: I - > J, there may be other points, but we regard them as connected through the shortest path of two points)
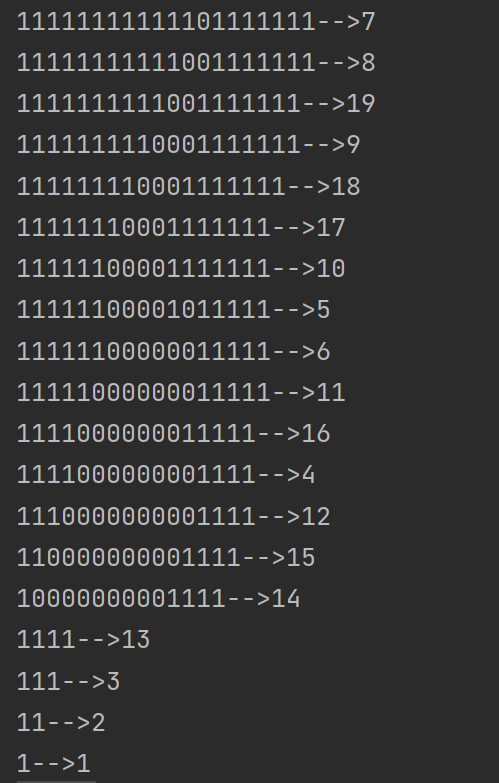

Look at this picture: the array on the right of the arrow indicates that bit i has changed to 0. When the last set becomes 0, we will win (repeat: start from bit 0)
if (index==-1) break;// You can also optimize the ending conditions yourself. Anyway, I like to write [HA HA]. It ends when the subscript does not change
At this time, we are only half successful,
0 1 2 3 13 14 15 12 4 11 16 11 5 6 5 10 17 18 9 19 8 7 0
Repeat again: 0 = > 1 or 10 = > 7 indicates only the shortest path. We have to find the existing points among them. At this time, we return to the path finding involved in the floyd algorithm. We can find them all through a for,
floydUtil.getPath(...): this function here will not add its last element to the array
Take a closer look at the following code to understand the whole process. I look forward to seeing the video at station b
//Find the path
/**
*
* @param p ((full route array)
* @param iii ((valid subscript of the above array)
* @param n (Number of vertices)
* @return (Return path (minimum)
*/
public void TSP_can_repeat_path(Double[][] dp,Double[][] dis,int[] path,int end,int n) {//end starts at 0
int s = (1<<n)-1;//The length of the path array is equal to the number of vertices (11... 111)
int idx = 0;//Initialize to 0
path[idx++] = end;//You're the last one
//System.out.println(Integer.toBinaryString(s));// Binary, I want to see what moths appear
while (true) {
s = s^(1<<end);//New status
//System.out.println(Integer.toBinaryString(s)+"-->"+end);
Double min = Double.MAX_VALUE;
int index = -1;
for (int i = 0; i < n; i++) {
if ( (s&(1<<i))!=0 && min > dp[s][i]+dis[i][end]) {
min = dp[s][i]+dis[i][end];
index = i;
}
}
if (index==-1) break;
path[idx] = index;
end = index;
idx ++;
}
for (int i = 0; i < (n / 2) - 1; i++) {
int tmp = path[i];
path[i] = path[n-1-i];
path[n-1-i] = tmp;
}
}
/**
*
* @param path (floyd (path after)
* @param p ((array to fill)
* @param initP ((path of the upper layer)
* @param idx (Record subscript)
*/
public void completePath(int[][] path,int[] p,int[] initP,int[] idx) {
int n = initP.length;
for (int i = 0; i < n-1; i++) {
int[] res = new int[n];
int[] index = new int[1];
floydUtil.getPath(path,initP[i],initP[i+1],res,index);
for (int j = 0; j < index[0]; j++) {
p[idx[0]++] = res[j];
}
}
p[idx[0]++] = initP[n-1];//Put the last point in
}
Here is the complete code I wrote
package com.lin.utils;
import org.springframework.beans.factory.annotation.Autowired;
import org.springframework.stereotype.Component;
@Component
public class FloydDPUtil {
@Autowired
private FloydUtil floydUtil;
/**
*
* @param p ((full route array)
* @param iii ((valid subscript of the above array)
* @param n (Number of vertices)
* @return (Return path (minimum)
*/
public Double TSP_can_repeat(int[] p,int[] iii,int n) {
//==================floyd
Double[][] distance = new Double[n][n];
int[][] path = new int[n][n];
floydUtil.floyd(distance,path);
//==================State compression DP
Double[][] dp = new Double[1<<n][n];
//Initialize dp array
for (int i = 0; i < 1<<n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j] = Double.MAX_VALUE;
}
}
dp[1][0] = 0.0;//Put point 0 into the collection
for (int s=1;s<(1<<n);s++) {
for (int i=0;i<n;i++) {
if ((s&(1<<i))!=0) {//It is vertex i that is added to the set
for (int j = 0; j < n; j++) {
if ((s&(1<<j))!=0&&i!=j) {
dp[s][i] = Math.min(dp[s][i],dp[s^(1<<i)][j]+distance[j][i]);
}
}
}
}
}
Double ans = Double.MAX_VALUE;
int idx = -1;
for (int i=1;i<n;i++) {//0 is the starting point, so don't join it
if (ans > dp[(1<<n)-1][i]+distance[i][0]) {
ans = dp[(1<<n)-1][i]+distance[i][0];
idx = i;
}
}
//Get the path to the array initP
int[] initP = new int[n+1];
TSP_can_repeat_path(dp,distance,initP,idx,n);
initP[n] = 0;
//Start parsing the contents and put them into the array p
completePath(path,p,initP,iii);
return ans;
}
//Find the path
public void TSP_can_repeat_path(Double[][] dp,Double[][] dis,int[] path,int end,int n) {//end starts at 0
int s = (1<<n)-1;//The length of the path array is equal to the number of vertices (11... 111)
int idx = 0;//Initialize to 0
path[idx++] = end;//You're the last one
//System.out.println(Integer.toBinaryString(s));// Binary, I want to see what moths appear
while (true) {
s = s^(1<<end);//New status
//System.out.println(Integer.toBinaryString(s)+"-->"+end);
Double min = Double.MAX_VALUE;
int index = -1;
for (int i = 0; i < n; i++) {
if ( (s&(1<<i))!=0 && min > dp[s][i]+dis[i][end]) {
min = dp[s][i]+dis[i][end];
index = i;
}
}
if (index==-1) break;
path[idx] = index;
end = index;
idx ++;
}
for (int i = 0; i < (n / 2) - 1; i++) {
int tmp = path[i];
path[i] = path[n-1-i];
path[n-1-i] = tmp;
}
}
/**
*
* @param path (floyd (path after)
* @param p ((array to fill)
* @param initP ((path of the upper layer)
* @param idx (Record subscript)
*/
public void completePath(int[][] path,int[] p,int[] initP,int[] idx) {
int n = initP.length;
for (int i = 0; i < n-1; i++) {
int[] res = new int[n];
int[] index = new int[1];
floydUtil.getPath(path,initP[i],initP[i+1],res,index);
for (int j = 0; j < index[0]; j++) {
p[idx[0]++] = res[j];
}
}
p[idx[0]++] = initP[n-1];//Put the last point in
}
}
Author: follow the wind
If you have any questions, you can talk to me in private qq:2338244917
You can pay attention to my b station account: leaves with the wind Jump = > leaves in the wind
It's already 2:30 a.m. after I finished writing, please give me a compliment

The number of csdn fans is about to exceed 300. Thank you for your support