HashMap capacity expansion mechanism
Previous review: Talk about HashMap 01 of jdk1.8
Last time we finished the put method, there was a way I did not elaborate, that is resize() method, which I personally think is the most beautiful but the most difficult part of HashMap. Next we will explain it slowly.
Review the member variables
transient Node<K,V>[] table;//Array of nodes transient int size; //Size of HashMap int threshold; //capacity final float loadFactor;//Load factor
resize() method
The resize() method is used for capacity expansion and initialization.
In this method, we should pay attention to old / newcap (old / new array length) and old / newthr (old / new capacity),
Look at the code. Part of the analysis has been written in the comments:
//When this method is called for the first time, both oldCap and oldThr are 0,
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
//This judgment can distinguish between initialization and capacity expansion
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
//Double the length and threshold
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1;
}
//If this is done, it is initialization
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
//If it can be executed here, that is, the parameterized structure is called, oldThr must be an integer power of 2
else {
//Running here means that the parameterless construction is called for initialization
//16
newCap = DEFAULT_INITIAL_CAPACITY;
//12
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
//From here, copy the data from the old array to the new array
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
//I personally think it's convenient here
oldTab[j] = null;
if (e.next == null)
//If the node has no subsequent nodes, the position in the new array is directly recalculated and inserted
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
//Detailed below
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
Old and new array data migration
In jdk1.7, each node must first calculate a perturbation function and then recalculate the subscript. In 1.8, this is the way
If there is no hash conflict, that is, a Node does not have a next Node, it will directly take the remainder with the new array length to obtain the subscript. If there is a hash conflict, it will start a cycle: first define four Node type variables:
loHead, loTail, hiHead, hitail (actually the abbreviation of low and high), then traverse the linked list, and sum the hash value of the key of each node with the length of the old array (assuming the nth power of 2). The purpose is to get whether the number of the nth bit is 0. If it is 0, put the node into the linked list with loHead as the head and loTail as the tail. Otherwise, put it into the linked list with hiHead as the head, A linked list with hiHead as the tail. The process is as follows:
hash: 0000 0000 1110 1111
oldCap:0000 0000 0000 1000
The result of phase and is not 0, so now there is only one node in the high linked list, and then traverse the next node of the node. Suppose
hash: 0000 0000 1110 0111
oldCap:0000 0000 0000 1000
If the result of phase and is 0, put the node into the low linked list, then traverse the next node, and perform the same operation. If the result is 1, put it into the tail of the high linked list, and repeat the above process until the next node is null.
Finally, put the low linked list in the original position and the high linked list in the original position + the length of the old array. Assuming that the length of the Node array is 16, now traverse to oldTable[2], and find that there is a hash conflict in table[2], with Node1 < 1, a >, Node2 < 2, b >, Node3 < 3, C >. After the above operations, the low linked list has Node2 and Node3, while the high linked list has Node1, so the new array is put in this way, Put Node2 in the place of newTable[2] (the next Node is Node3), and Node1 in the place of newTable[2+16]. End.
Draw a picture to deepen your understanding
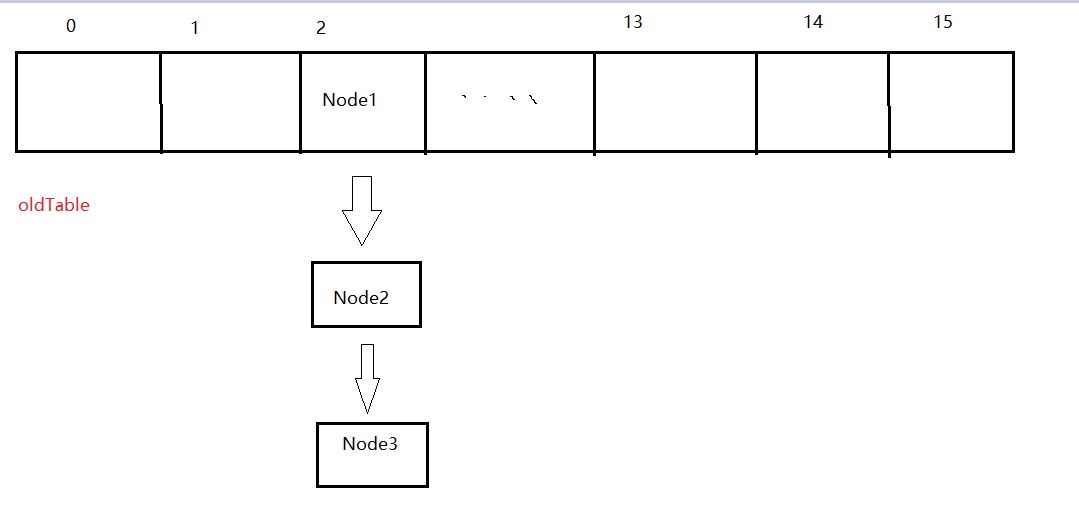
After the above calculation
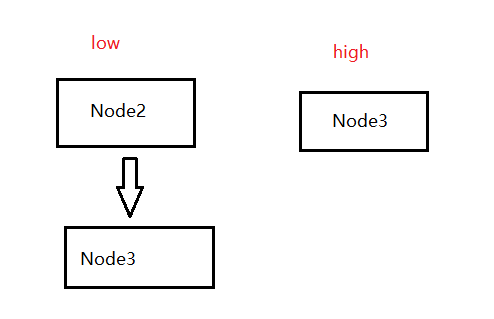
last
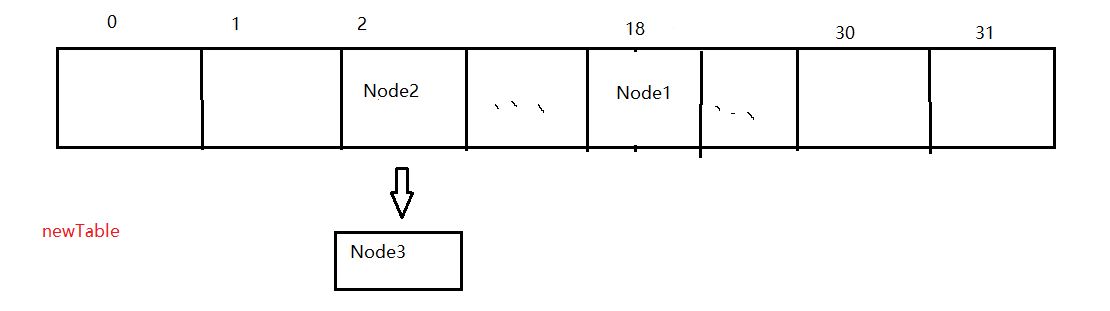
other
In fact, HashMap embodies the idea of lazy loading. After we call the construction method, the table in the member variable has not been assigned, that is, at this time, table=null. It will not be initialized until the put method is executed for the first time.