Merge sort

🎈🎆🎇 preface:

1, Priority queue heap PriorityQueue

2, Deep understanding of fast scheduling and optimization

The number of times that merge sort is often tested in the eight sorts can be said to be among the best, and its status is also very high, which can not be ignored. In the sort of quick sort, merge sort and heap sort, the interviewer will basically ask about one of them. The time complexity is also the fastest in the sort, so we must master the knowledge of the front quick sort( Quick sort )And heap sorting knowledge( Heap sort ), it will not be too abstract to merge and understand

🍕🍔🍟 Merge sort:

Merge Sort is based on Merge An effective and stable operation Sorting algorithm , the algorithm is adopted Divide and conquer (Divide and Conquer) is a very typical application. The ordered subsequence merge , get completely ordered sequence ； That is, each subsequence is ordered first, and then the subsequence segments are ordered. If two ordered tables are combined into one ordered table, it is called Two way merging.

🚗🚓🚕 Basic idea:

The idea of merge sort is actually very simple. It uses the idea of divide and conquer to define a mid, so as to separate the left and right. Each time, it recurses like a binary tree, divides it into numbers one by one, and then sort in the merge.

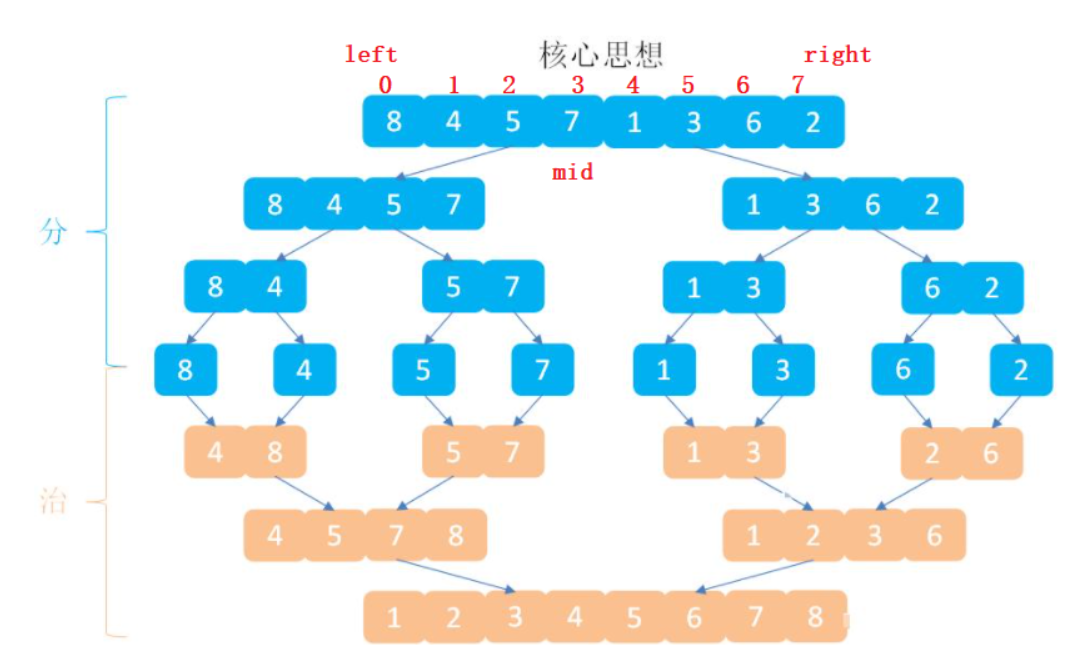
1, Merge two ordered arrays

To complete merge sort, we must first know how to merge two ordered arrays into one array, which is also the core idea of merge sort

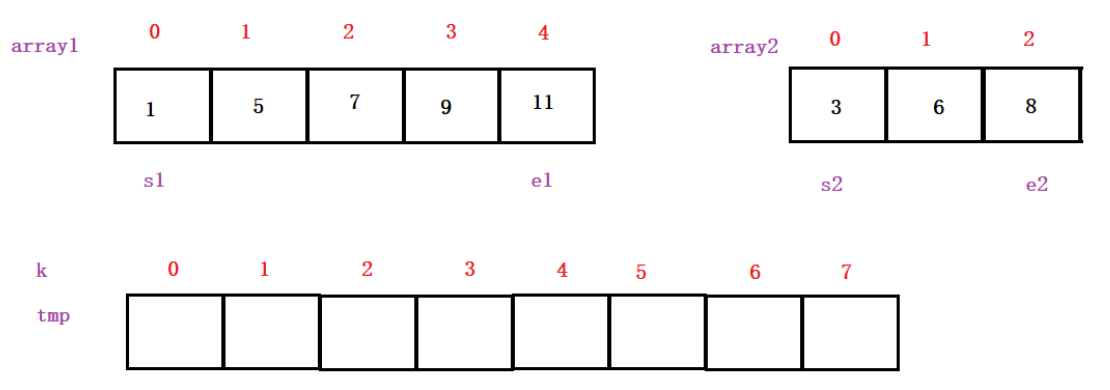
First, there are two ordered arrays. start and end are defined. The two arrays s1 and s2 are compared. The smaller one is put into the tmp array. k is the index of the tmp array.

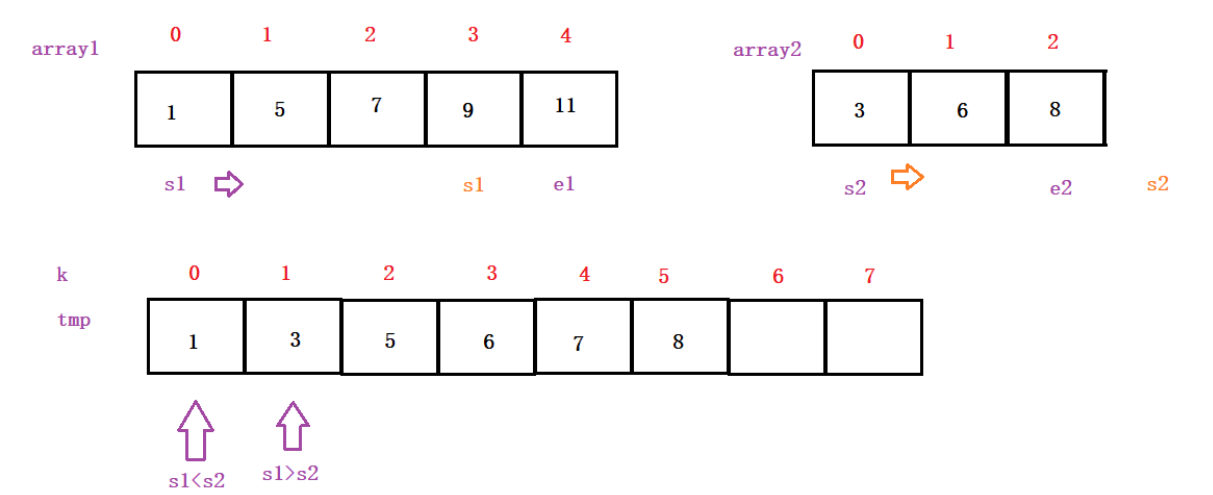
At this point, s2 has been completed, and the rest of s1 can be put down directly.

🍰🎂🍪 Core code: the code is still very simple 😁😁😁😁

public static int[] mergeArray(int[] array1,int[] array2) {
        int[] tmp = new int[array1.length+array2.length];//The length of the new array is the sum of array1 and array2
        int k = 0;//Subscript of tmp array

        int s1 = 0;
        int e1 = array1.length-1;//Can not write

        int s2 = 0;
        int e2 = array2.length-1;//Can not write

        //Comparison of two arrays
        while (s1 <= e1 && s2 <= e2) {
            if(array1[s1] <= array2[s2]) {
                tmp[k++] = array1[s1++];
            }else {
                tmp[k++] = array2[s2++];
            }
        }
        //Put the rest directly into the tmp array
        while (s1 <= e1) {
            tmp[k++] = array1[s1++];
        }
        while (s2 <= e2) {
            tmp[k++] = array2[s2++];
        }
        return tmp;
    }

Now that our core idea code has been written, there is only the framework left for merging and sorting. This time, we use the idea of recursion;

2, Recursive version

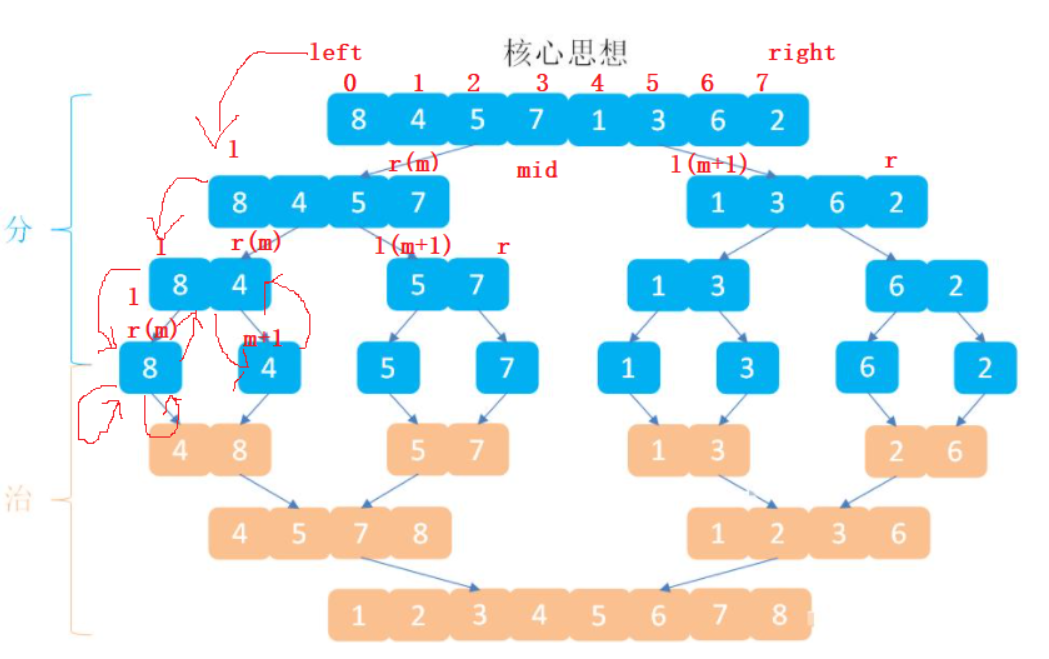
The point to note here is that when the score is divided, the left ends with mid and the right ends with mid+1

code:

//To be sorted interval
    public static void mergeSortInternal(int[] array,int left,int right) {
        if(left>=right) {//Termination conditions
            return;
        }

        int mid=(left+right)/2;
        mergeSortInternal(array,left,mid);
        mergeSortInternal(array,mid+1,right);
    }

The above foreshadowing is almost the same. Just apply the above code,

Full code:

public static void merge(int[] array,int left,int right,int mid) {
        int[] tmp=new int[right=left+1];
        int k=0;

    //Start divide and conquer, mid is the end on the left
        int s1=left;
        int e1=mid;

    //mid+1 is the beginning of the right
        int s2=mid+1;
        int e2=right;

        while (s1<=e1 && s2<=e2) {
            if(array[s1]<=array[s2]) {
                tmp[k++]=array[s1++];
            } else {
                tmp[k++]=array[s2++];
            }
        }

        while (s1<=e1) {
            tmp[k++]=array[s1++];
        }
        while (s2<=e2) {
            tmp[k++]=array[s2++];
        }

        for (int i = 0; i < k; i++) {
            array[i+left]=tmp[i];//!!!!!!!!
            //It should be noted here that it cannot be written as array[i]=tmp[i], because when it is divided to the right, it ends with mid+1 subscript,
        }
    }
    //To be sorted interval
    public static void mergeSortInternal(int[] array,int left,int right) {
        if(left>=right) {//Termination conditions
            return;
        }

        int mid=(left+right)/2;
        mergeSortInternal(array,left,mid);
        mergeSortInternal(array,mid+1,right);
        merge(array,left,right,mid);
    }

    public static void mergeSort(int[] array) {
        mergeSortInternal(array,0,array.length-1);
    }

Here is a point to note:

When putting the array in tmp into the array in array, it must be written as array[i+left]=tmp[i];

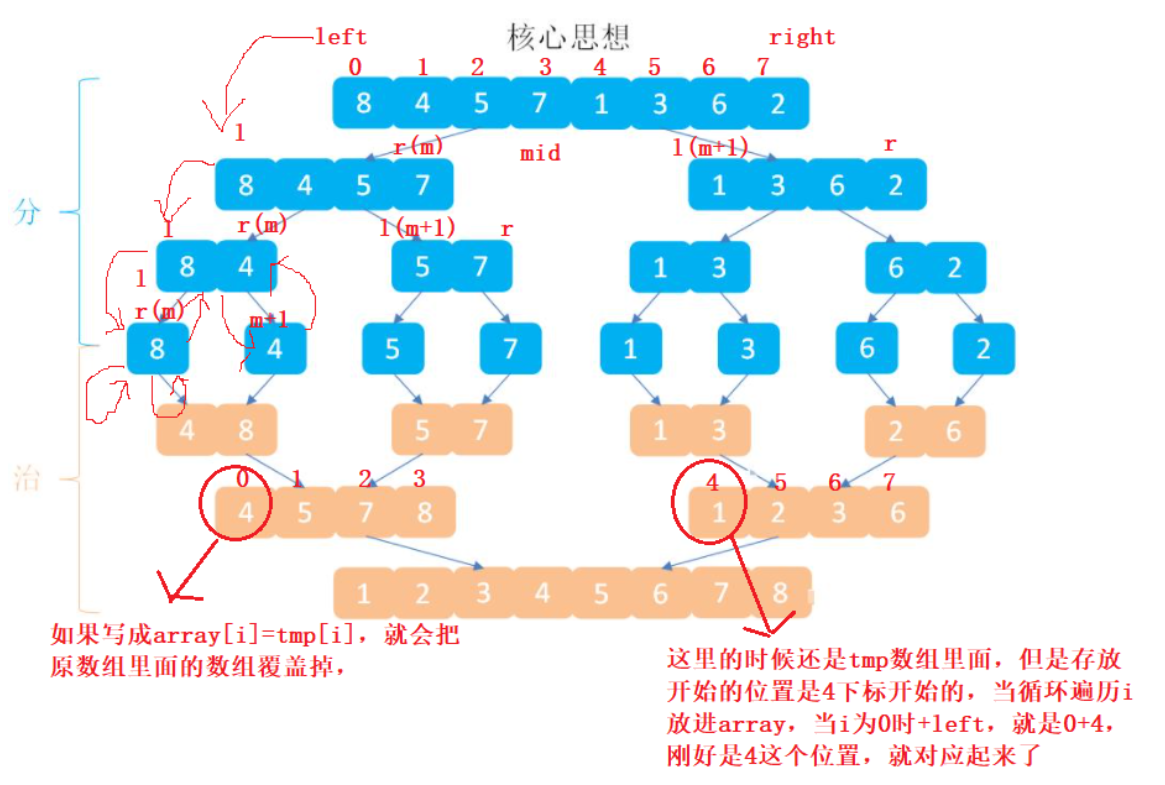
If it is written as array[i]=tmp[i], the array in the original array will be overwritten,

3, Performance analysis

Time complexity	Spatial complexity
O(n * log(n))	O(n)

The time complexity is equivalent to the height of binary tree + traversal, and the space complexity is O (n) because of new tmp

4, Non recursive version

The non recursive version is troublesome to understand, because it will consider many situations and pay attention to many boundary problems. It is really annoying. If you want to write merge sort, you'd better write recursion directly. If you have requirements, you can only do it 🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤🐱 ‍ 👤

First, two arrays must be merged, but each array will be divided into gap, first 1 group, then 2 groups, and then 4 groups, which is similar to the above figure.

😎🙂🤗 Group code:

public static void mergeSort(int[] array) {
        for (int gap = 1; gap < array.length; gap*=2) {
            merge2(array,gap);
        }
    }

As shown in the figure, the positions of S1, E1, S2 and e2 can be determined, but e2 may need to pay attention to:

Therefore, when e2 is greater than the length of the array, directly len-1,

😶😑😐 Location code:

public static void merge2(int[] array,int gap) {

        int[] tmp = new int[array.length];
        int k = 0;
        int s1 = 0;
        int e1 = s1+gap-1;
        int s2 = e1+1;
        int e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
}

The following is the comparison of two arrays. Two arrays must have two segments, so there will be a judgment condition. The comparison of two arrays has also been written and used directly

code:

 while (s2 < array.length) {//This is the judgment condition that there must be two segments
            while (s1 <= e1 && s2 <= e2) {
                if (array[s1] <= array[s2]) {
                    tmp[k++] = array[s1++];
                }else {
                    tmp[k++] = array[s2++];
                }
            }
            while ( s1 <= e1 ) {
                tmp[k++] = array[s1++];
            }
            while (s2 <= e2) {
                tmp[k++] = array[s2++];
            }
        }

Because it is not recursive, after the two-stage array is compared, the position of the next two-stage array must be determined. Therefore, it is necessary to write:

s1 = e2+1;
e1 = s1+gap-1;
s2 = e1+1;
e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;

However, after writing the above code, several situations will occur:

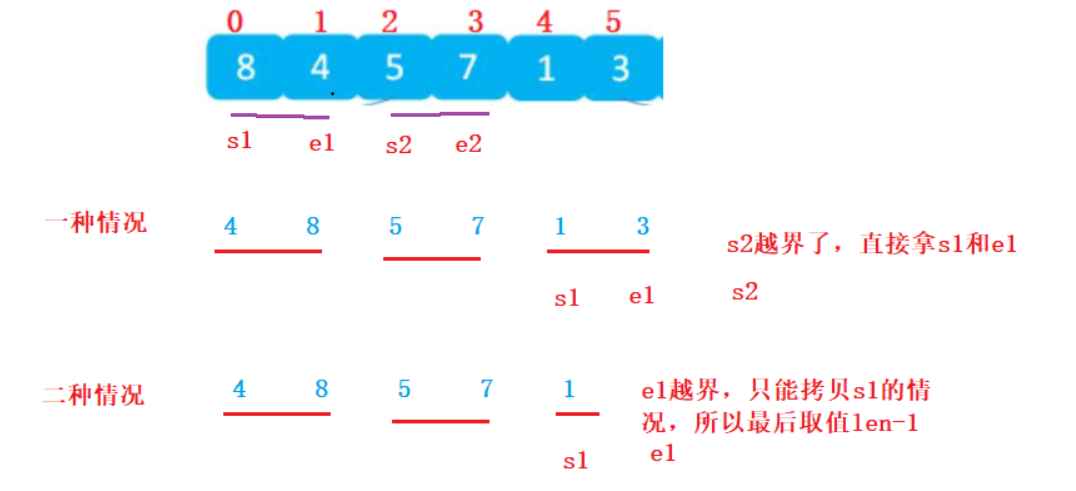
The above two situations will occur. Finally, move the redundant. In the final analysis, the final value range is len-1;

Full code:

 public static void merge2(int[] array,int gap) {
        int[] tmp = new int[array.length];
        int k = 0;

        int s1 = 0;
        int e1 = s1+gap-1;
        int s2 = e1+1;
        int e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;
        //There must be two paragraphs, judging by s2
        while (s2 < array.length) {

            while (s1 <= e1 && s2 <= e2) {
                if (array[s1] <= array[s2]) {
                    tmp[k++] = array[s1++];
                }else {
                    tmp[k++] = array[s2++];
                }
            }

            while ( s1 <= e1 ) {
                tmp[k++] = array[s1++];
            }
            while (s2 <= e2) {
                tmp[k++] = array[s2++];
            }

            s1 = e2+1;
            e1 = s1+gap-1;
            s2 = e1+1;
            e2 = s2+gap-1 >= array.length ? array.length-1 : s2+gap-1;

        }

        //Only the last paragraph is left. Considering multiple situations, in the final analysis, the value range is len-1
        while (s1 <= array.length-1) {
            //s1 < = e1 also needs to be considered when s1 exists but e1 does not exist, s1 < = array.length-1
            tmp[k++] = array[s1++];
        }
        for (int i = 0; i < k; i++) {
            array[i] = tmp[i];
        }
    }

 public static void mergeSort1(int[] array) {

        for (int gap = 1; gap < array.length; gap*=2) {
            merge2(array,gap);
        }
    }

The above is all the content of this post, which must be fully mastered. Among the seven sorting, fast sorting, stacking and merging are often tested. Fast sorting appears the most frequently, followed by stacking and merging, followed by direct insertion, hill, selection and bubbling. Relatively speaking, the code and thought should be simpler. Hill sorting is a little difficult to understand, but it is almost not tested. Master We still need to be familiar with their time complexity, space complexity and stability, as well as their main implementations. We have summarized the merging and sorting code. If you want to see the whole code, you can click my Github , it's all sorted code.

Iron juice, I think the author's writing is good, you can praise it ❤🧡💛💚💙💜🤎🖤🤍💟， Collection and attention, your support is the biggest driving force for me to write a blog