Links: http://codeforces.com/problemset/problem/232/B

Implication: Give a large matrix of n*m (m >= n), put a point in the matrix to satisfy the number of k points for each small matrix of n*n.

Ideas for problem solving:

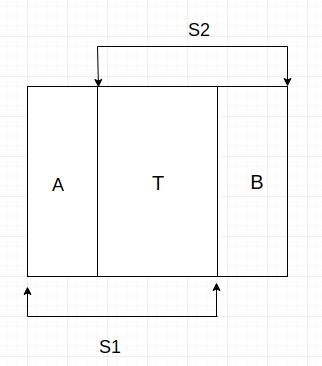
For a matrix S1 A of n*n is the number of points i n the left column, B is the number of points i n the right column of S2, so there is A+T=B+T. So when the number of points i n column I of the first n*n matrix is determined, n+i, n+2*i... The number of points will be determined, so the problem is transformed into finding the number of points i n each column of the first n * n matrix. When dp[i][j] is the number of J points i n column i, it is not difficult to deduce that dp[i][j]= min(n,j)x=0dp[i 1][j x] Cxn. It is described i n language that the number of J points i n column I is determined by column i-1 multiplying j-x points i n column n to select x points. Of course, Cxn here should take into account the following N + i, n + 2 * i... Point effect.
Code:

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>

#define LL long long
using namespace std;
const int MOD = 1e9 + 7;
const int Max = 120;
LL C[Max][Max];
LL Z[Max][Max];
LL dp[Max][15000];

void get_combinations() {//Recursion of Combination Number
    for (int a = 1; a <= 100; a++) {
        C[a][0] = C[a][a] = 1;
        for (int b = 1; b < a; b++) {
            C[a][b] = (C[a - 1][b - 1] + C[a - 1][b]) % MOD;//For a point, if it is determined to be C[a - 1][b - 1], it is determined not to be C[a - 1][b]
        }
    }
}

LL pow_MOD(LL n, LL m) {//Counting
    LL ans = 1;
    while (m) {
        if (m & 1)ans = (ans * n) % MOD;
        n = (n * n) % MOD;
        m >>= 1;
    }
    return ans;
}

int main() {
    LL n, m, k;
    get_combinations();
    scanf("%lld%lld%lld", &n, &m, &k);
    for (LL a = 1; a <= n; a++) {//Determining the number of b in column a will have an impact on the future
        for (LL b = 0; b <= n; b++) {//When the remaining number of m%n is still enough a, it will affect the latter m/n+1 column, otherwise it will affect the m/n column.
            Z[a][b] = pow_MOD(C[n][b], m / n +  + (m % n >= a));
        }
    }
    dp[0][0] = 1;
    for (LL a = 1; a <= n; a++) {//For line a, the state of b points is determined.
        for (LL b = 0; b <= min(k, n * a); b++) {
            for (LL c = 0; c <= min(b, n); c++) {
                dp[a][b] = (dp[a][b] + dp[a - 1][b - c] * Z[a][c]) % MOD;
            }
        }
    }
    printf("%lld\n", dp[n][k]);
    return 0;
}