01 reconstruction of binary tree
Title Description
Enter the results of the preorder traversal and inorder traversal of a binary tree, and rebuild the binary tree. It is assumed that the results of the input preorder traversal and preorder traversal do not contain duplicate numbers. For example, if the sequence {1,2,4,7,3,5,6,8} and the sequence {4,7,2,1,5,3,8,6} are input, the binary tree will be reconstructed and returned.
Train of thought:
In the previous traversal sequence of a binary tree, the first number is always the value of the root node of the tree. But in the middle order traversal sequence, the value of the root node is in the middle of the sequence, the value of the node of the left subtree is on the left side of the value of the root node, and the value of the node of the right subtree is on the right side of the value of the root node. Therefore, we need to scan the middle order traversal sequence to find the value of the root node.
As shown in the figure below, the first digit 1 of the preamble traversal sequence is the value of the root node. Scanning the middle order traversal sequence can determine the location of the value of the root node. According to the characteristics of the middle order traversal, the three numbers in front of the value 1 of the root node are the values of the left subtree node, and the numbers behind the value 1 are the values of the right subtree node.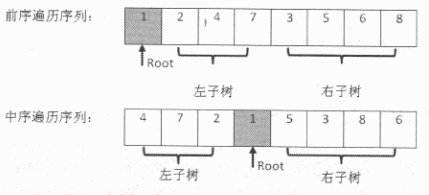
Similarly, in the sequence of traversal, the three numbers behind the root node are the values of the three left subtree nodes, and then all the numbers behind are the values of the right subtree nodes. In this way, we find the corresponding subsequences of left and right subtrees in the two sequences of preorder traversal and middle order traversal.
Now that we have found the preorder traversal sequence and the middle order traversal sequence of the left and right subtrees respectively, we can use the same method to construct the left and right subtrees respectively. In other words, the next thing can be done recursively
Question: how to express it? https://blog.csdn.net/weixin_38339143/article/details/79897670
class TreeNode: def __init__(self, x): self.val = x self.left = None self.right = None class Solution: # Returns the TreeNode root node of the construct def reConstructBinaryTree(self, pre, tin): # write code here if len(pre)==0: return None root_data = TreeNode(pre[0])#Define the root as a node i=tin.index(pre[0])#i=tin.index(root_data.val)#Find the location to separate the left and right subtrees #Returns the index of the root node root_data.left = self.reConstructBinaryTree(pre[1:1+i],tin[:i]) root_data.right = self.reConstructBinaryTree(pre[1+i:],tin[i+1:]) return root_data # instantiation if __name__=='__main__': pre=[1,2,4,7,3,5,6,8] tin=[4,7,2,1,5,3,8,6] demo = Solution() print(demo.reConstructBinaryTree(pre,tin))
Next node of 02 binary tree
Title Description
Given a binary tree and one of its nodes, find the next node in the middle order traversal order and return. Note that the nodes in the tree contain not only left and right child nodes, but also pointers to the parent nodes.
Analyze the next node of the binary tree. There are the following situations in total:
1. If the binary tree is empty, it returns NULL;
2. If the right child of the node exists, set a pointer to start from the right child of the node and follow the pointer to the left child to find the leaf node as the next node;
3. The node is not the root node. If the node is the left child of its parent node, the parent node will be returned; otherwise, continue to traverse the parent node of its parent node, repeat the previous judgment, and return the result. The code is as follows
class Solution: def GetNext(self, pNode): if pNode.right:#Right subtree p=pNode.right while p.left: p=p.left return p while pNode.next:#If there is no right subtree, the node whose first current node is the left child of the parent node will be found if(pNode.next.left==pNode): return pNode.next pNode = pNode.next#Traverse up the parent node return #Return null if the root node is not found
03 symmetric binary tree
Please implement a function to judge whether a binary tree is symmetric. Note that if a binary tree is the same as the image of the binary tree, it is defined as symmetric.
/*Idea: first, the root node and its left and right subtrees, the left subtree and the right subtree of the left subtree are the same
- The right subtree of the left subtree is the same as the left subtree of the right subtree. The left and right nodes are compared recursively, and then the left and right branches of the left and right nodes are compared recursively
- It is also possible to use stack or queue to access all levels of sub tree root nodes
Recursive Method # -*- coding:utf-8 -*- # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def isSymmetrical(self, pRoot): if pRoot is None: return True return self.Traversal(pRoot.left,pRoot.right) def Traversal(self,left, right): if left is None and right is None: return True elif left and right and left.val ==right.val: return self.Traversal(left.left,right.right) and self.Traversal(left.right,right.left) else: return False
03 - print binary trees in zigzag order
Please implement a function to print the binary tree in zigzag, that is, the first line is printed from left to right, the second layer is printed from right to left, the third line is printed from left to right, and so on.
We can use one queue, one stack or two stacks. I use two stacks to realize it. The idea is simple.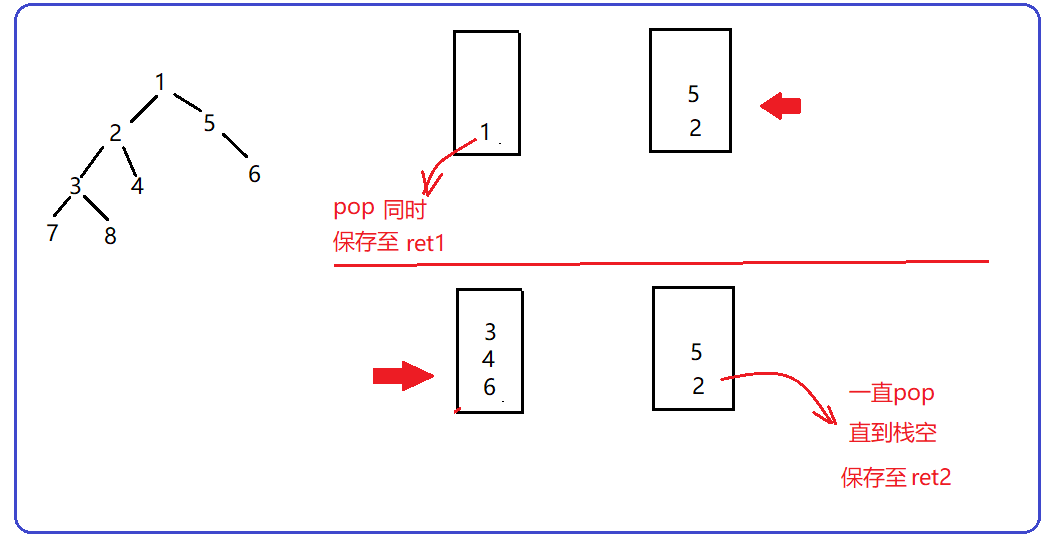
# -*- coding:utf-8 -*- # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def Print(self, pRoot): if pRoot is None: return [] queue=[] queue.append(pRoot)#Store root node in queue result=[]#How many layers does the storage tree have, 1,2, 3,4 and so on while len(queue)!=0: res=[] #Storage nodes of each layer nextStack=[] #Store left and right subtree nodes for i in queue: res.append(i.val) if i.left: nextStack.append(i.left) if i.right: nextStack.append(i.right) queue=nextStack result.append(res) returnResult=[] for i, v in enumerate(result): if i%2==0: returnResult.append(v) else: returnResult.append(v[::-1]) return returnResult
04 - print binary tree into multiple lines
Title Description
The binary tree is printed from top to bottom, and the nodes of the same layer are output from left to right. Output one line per layer.
# -*- coding:utf-8 -*- # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def Print(self, pRoot): if pRoot is None: return [] queue=[] queue.append(pRoot)#Store root node in queue result=[]#How many layers does the storage tree have, 1,2, 3,4 and so on while len(queue)!=0: res=[] #Storage nodes of each layer nextStack=[] #Store left and right subtree nodes for i in queue: res.append(i.val) if i.left: nextStack.append(i.left) if i.right: nextStack.append(i.right) queue=nextStack result.append(res) #Here we get the nodes corresponding to each layer return result
05 serialized binary tree
Title Description
Please implement two functions to serialize and deserialize binary tree
Topic analysis: is serialization hierarchical traversal
What does deserialization mean?
For serialization: use preorder traversal to recursively convert binary tree values to characters, and at each node of the binary tree
When it is not empty, add a ',' as the division after the character obtained by converting val. For empty nodes, use '×' instead.
2. For deserialization: recursively create a binary tree using the characters in the string in the order of precedence (Note:
In recursion, the parameter of the recursion function must be char * *, so as to ensure that the pointer to the string will
Move with recursion!!! )
# -*- coding:utf-8 -*- # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def __init__(self): self.flag = -1 def Serialize(self, root): # write code here if not root: return '#,' return str(root.val)+','+self.Serialize(root.left)+self.Serialize(root.right) def Deserialize(self, s): # write code here self.flag += 1 l = s.split(',') if self.flag >= len(s): return None root = None if l[self.flag] != '#': root = TreeNode(int(l[self.flag])) root.left = self.Deserialize(s) root.right = self.Deserialize(s) return root
06 print binary tree
Title Description
Each node of the binary tree is printed from top to bottom, and the nodes of the same layer are printed from left to right
Idea: the level traversal of binary tree first calculates the left and right subtrees of the root node, and recycles recursion with the help of a queue
The idea is very clear, using two queues, one storage node and one storage value. First add the root node to the queue, and then traverse the elements in the queue. In the process of traversing, access the left and right nodes of the element, and then add the left and right child nodes to the queue
The routine of extensive search is to use a queue to save the elements of the layer to be searched, and then search one by one;
1. Queue the first element
2. Take the first element when the queue is not empty
3. Add next level elements to the end of the team
4. Go to step 2 until the queue is empty
Root is the root node
# -*- coding:utf-8 -*- # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: # Returns the list of values of each node from top to bottom, for example: [1,2,3] def PrintFromTopToBottom(self, root): if root is None: return [] queue=[] result=[] queue.append(root) while len(queue)>0: root=queue.pop(0) result.append(root.val) if root.left is not None: queue.append(root.left) if root.right is not None: queue.append(root.right) return result
07 - judgment results
Input an integer array to determine whether the array is the result of the subsequent traversal of a binary search tree. If Yes, output Yes; otherwise, output No. Suppose that any two numbers of the input array are different from each other.
Train of thought:
- The post order traversal of a binary tree starts with the left node, then the right node, and finally the root node
2. Binary search tree is a search tree formed by binary search of an ordered array. It refers to an empty tree or a binary tree with the following properties:
If the left subtree of any node is not empty, the values of all nodes on the left subtree are less than the values of its root nodes; if the right subtree of any node is not empty, the values of all nodes on the right subtree are greater than the values of its root nodes;
The left and right subtrees of any node are also binary search trees;
For example, we all know that the middle order traversal of the binary search tree in the following figure can be restored to an ordered array, while the result of the second order traversal of the binary tree in the figure is [3, 2, 4, 6, 8, 7, 5]. Next, I will analyze the law of this array. The last element of the array is the root of the whole binary tree. In addition, according to the first two properties of the search binary tree, the left subtree is smaller than the root, and the right subtree is larger than the root. The left and right subtrees also conform to the whole rule, so we can recursively implement array judgment.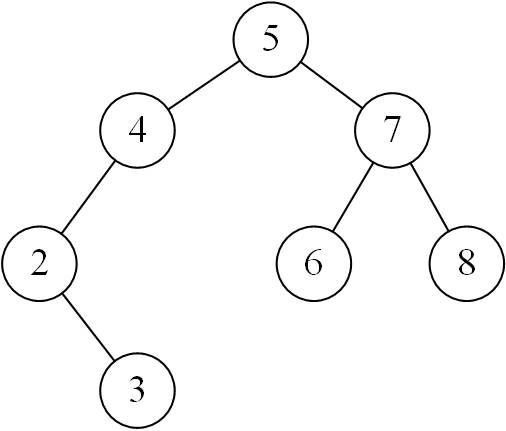
# -*- coding:utf-8 -*- class Solution: def VerifySquenceOfBST(self, sequence): # write code here if len(sequence) == 0: return False else: root = sequence[-1] del sequence[-1] lefttree = [] righttree =[] # Left subtree and right subtree boundary splitindex = -1 for i in range(len(sequence)): # If the value is less than the root node, it is classified as the left subtree if sequence[i] < root: lefttree.append(sequence[i]) splitindex = i else: break for i in range(splitindex+1, len(sequence)): # If the right subtree has a value less than the root node, it is not a binary search tree if sequence[i] > root: righttree.append(sequence[i]) else: return False if len(lefttree) <= 1: left = True else: # Recursively judging left subtree left = self.VerifySquenceOfBST(lefttree) if len(righttree) <= 1: right = True else: right = self.VerifySquenceOfBST(righttree) return left and right
The k-th node of 08 binary search tree
Given a binary search tree, please find the k-th smallest node. For example, in (5, 3, 7, 2, 4, 6, 8), the value of the third summary point in the order of node value size is 4.
Thought analysis:
Do a deep traversal - then save it to the list,
# -*- coding:utf-8 -*- # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: # Return to the corresponding node TreeNode def KthNode(self, pRoot, k): self.res=[] self.dfs(pRoot) if 0<k<=len(self.res): return self.res[k-1] else: return None def dfs(self,root): if not root:return self.dfs(root.left) self.res.append(root) self.dfs(root.right)
The substructure of a tree
Input two binary trees a and B to determine whether B is a substructure of A. (ps: we agree that an empty tree is not a substructure of any tree)
**>Solutions to problems
My detour is to get the pre order traversal array and the mid order traversal array of A and B respectively -- >
Compare B's preorder traversal array with A's preorder traversal array; compare B's preorder traversal array with A's preorder traversal array;
The correct way of thinking is to traverse the binary tree a, locate the possible position of the root node of B in a -- > after positioning, verify whether B is the substructure of the current position of A. * *
The idea of this paper is to judge the substructure. First, it is necessary to judge whether the root nodes of the two trees are the same. If they are different, call their left subtree and B tree recursively. If they are still different, call their right subtree and B tree recursively. If they are different, return false.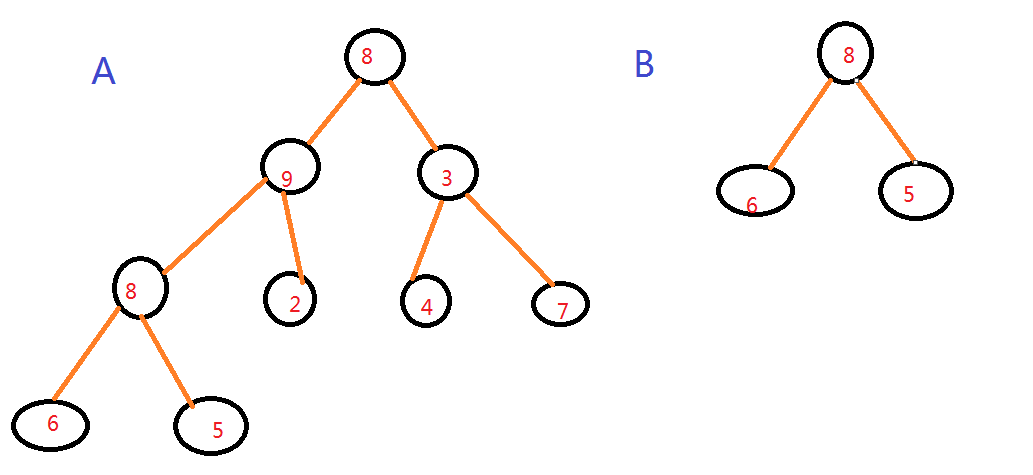
Original: https://blog.csdn.net/u010005281/article/details/79460325 -- complete test code
1. First find the same node as the root node of B in A
2. After finding other nodes in the corresponding position, traverse them until the nodes in B are traversed, all of which are the same, then B is the subtree of A
3. If the nodes in the corresponding position are different, exit continues to search for the same node in A as the root node in B, and repeat the steps until any binary tree is empty to exit
# -*- coding:utf-8 -*- # class TreeNode: # def __init__(self, x): # self.val = x # self.left = None # self.right = None class Solution: def HasSubtree(self, pRoot1, pRoot2): if pRoot1==None or pRoot2==None: return False result=False if pRoot1.val==pRoot2.val: result=self.isSubtree(pRoot1,pRoot2) if result==False: result=self.HasSubtree(pRoot1.left,pRoot2)|self.HasSubtree(pRoot1.right,pRoot2) return result def isSubtree(self,root1,root2): #This function determines whether other nodes are the same after finding the same node as the root node of the sub tree if root2==None: return True if root1==None: return False if root1.val==root2.val: return self.isSubtree(root1.left,root2.left)& self.isSubtree(root1.right,root2.right) return False
Is it a balanced binary tree
Title Description
Input a binary tree to determine whether the binary tree is a balanced binary tree.
Idea: balanced binary tree is defined as a binary tree whose height difference between left and right subtrees of any node does not exceed 1.
According to the definition, it is easy to get the height of left and right subtrees, and then judge. Recursive writing.
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def IsBalanced_Solution(self, pRoot):
if not pRoot: return True
left = self.TreeDepth(pRoot.left)
right = self.TreeDepth(pRoot.right)
if abs(left - right) > 1:
return False
return self.IsBalanced_Solution(pRoot.left) and self.IsBalanced_Solution(pRoot.right)
def TreeDepth(self, pRoot):
if not pRoot: return 0
left = self.TreeDepth(pRoot.left)
right = self.TreeDepth(pRoot.right)
return max(left, right) + 1
Comparison: find the depth of binary tree (Python code)
def TreeDeep(self, pRoot):
if not pRoot:
return 0
left = self.TreeDeep(pRoot.left)
right = self.TreeDeep(pRoot.right)
return left+1 if left>right else right+1
!
Binary tree depth and balanced binary tree
Title Description
Enter a binary tree to find the depth of the tree. The nodes (including root and leaf nodes) passing from root node to leaf node form a path of the tree. The longest path length is the depth of the tree.
Links: https://www.nowcoder.com/questionTerminal/435fb86331474282a3499955f0a41e8b
//Source: niuke.com
//To find the depth of a tree, we can start from the level traversal
//Hierarchical traversal can be done using queues or recursion, so there are two ways
//Method 1: use queue
class Solution:
# level traversal
def levelOrder(self, root):
# write your code here
# Store the results of the last level traversal
res = []
# Layer number
count = 0
# Returns an empty list if the root node is empty
if root is None:
return count
# Simulate a queue storage node
q = []
# Team root first
q.append(root)
# When the list is empty, the loop ends
while len(q) != 0:
# Using lists to store peer nodes
tmp = []
# Record the number of nodes in the same layer
length = len(q)
for i in range(length):
# Queue out nodes of the same layer in turn
r = q.pop(0)
if r.left is not None:
# Non empty left children join the team
q.append(r.left)
if r.right is not None:
# Non air right children join the team
q.append(r.right)
tmp.append(r.val)
if tmp:
count += 1 # Statistical layer
res.append(tmp)
return count
def TreeDepth(self, pRoot):
# write code here
# Use hierarchy traversal
# Return 0 when the tree is empty
if pRoot is None:
return 0
count = self.levelOrder(pRoot)
return count
//Method 2: use recursive method
class Solution:
def TreeDepth(self, pRoot):
# write code here
# Use hierarchy traversal
# Return 0 when the tree is empty
if pRoot is None:
return 0
# Method 2: use recursion
# If the tree has only one node, its depth is 1. If the root node has only left subtree and no right subtree,
# Then the depth of the tree is the depth of the left subtree plus 1; similarly, if only the right subtree has no left subtree,
# Then the depth of the tree is the depth of the right subtree plus 1. If there are both left and right subtrees,
# Then the depth of the tree is the maximum of the left and right subtrees plus 1
count = max(self.TreeDepth(pRoot.left), self.TreeDepth(pRoot.right)) + 1
return count
Binary trees and paths of a certain value
Title Description
Input the root node and an integer of a binary tree, and print out all paths whose sum of node values in the binary tree is the input integer. Path is defined as a path from the root node of the tree to the node that the leaf node passes through. (Note: in the list of returned values, the array with large array length is first)
not x means if x is false, then True, else False
There are often three main ways to judge whether a variable is None in the code:
The first is if x is None;
The second is if not x:;
The third is if not x is None
Train of thought 1: – recursion
First of all, we need to understand the meaning of the question, which is from the root node to the child node.
1. If only the root node or the leaf node is found, we will return its corresponding val value
2. If it is not a leaf node, we recurse the left and right subtrees of the root node until we find the leaf node. Then traversal returns the sequence composed of val corresponding to leaf node and parent node to the previous layer; if no path is found, it actually returns the sequence, just []
# -*- coding:utf-8 -*-
# class TreeNode:
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
class Solution:
def FindPath(self, root,target_number):
result =[]
if not root:
return result
if not root.left and not root.right and root.val == target_number:
return [[root.val]]
else:
left = self.FindPath(root.left,target_number - root.val)
right = self.FindPath(root.right,target_number - root.val)
for item in left+right:
result.append([root.val]+item)
return result
Original: https://blog.csdn.net/zjxxyz123/article/details/79699575
Train of thought 2: similar to train of thought 1, but put forward some precautions of python
This is a DFS problem, which can also be regarded as a preorder traversal problem. In a binary tree, DFS is equivalent to preorder traversal
First of all, a "subtraction" idea is adopted. When checking whether the sum of paths formed by a tree from root to leaf node is target, the value root.val of the current root node is set first
Add path, and then check its left subtree (if not empty) to see whether the sum of paths from the root of the left subtree to the leaf node is target - root.val (recursive),
Then the same way to recursively check the right subtree (if not empty), which is the general idea. But the trouble with this problem is that it requires recording all paths that meet the standard, which uses the characteristics of dfs.
But there's another trouble. The first order traversal is left first and then right. After checking the left subtree, the path will be modified, and then the right subtree will be searched. How can the path be restored to the state where the left subtree was not checked before?
At the beginning, I made a copy of the current path every time I went to the fork. I used the original path to continue the recursion of the left subtree and the copy path to recursion of the right subtree. In this way, the left subtree had an impact on the results of the right subtree, but this caused a lot of copies and wasted space
A better way is to set the path as global, and then the process of dfs is the process of first order traversal. Once the path is traversed to the leaf node, the last node of the path will be removed. In this way, the value will be added to the path when the recursion is carried out layer by layer, and the last element of the path will be removed one by one during the recursion. In this way, the path recovery is completed by the recursive feature.
For example, for trees 10, 5, 12, 5, 7, Chen, Chen, Chen, Chen, Chen, Chen, Chen (sequence traversal), the path change process is 10, 5, 5, 10, 5
10,5,7 >>10,5 >>10 >>10,12 >>10 >> null
When we finally traverse to the leaf node, if we find a path that meets the requirements, we add the path to the result set. Because java adds a reference and the path is constantly changing, we need to create a new copy of the current path to prevent the added paths from being the same (the state of the final path).
Of course, this problem can also use the idea of addition to see whether target can be added in the process of dfs
Because the meaning of the question does not say that the node values are all positive numbers, so it is necessary to recurse to the root node to determine whether the path can add a target, but not to the middle node to add > = target. It is considered that the path cannot be added. If the path sequence has 0 or negative numbers, the target can also be added.
Experience and lesson: deeply understand the usage of DFS, deeply understand how recursion recovers path, consider from traversal first, how recursion works step by step, and how to return step by step
Finally added to the result set, what must be added is the copy recursion of path, the use of global variables
# -*- coding:utf-8 -*-
class Solution:
# Return to the two-dimensional list. Each list inside represents the path found
def FindPath(self, root, expectNumber):
# write code here
if not root:
return []
ret = []
path = []
self.Find(root, expectNumber, ret, path)
# print ret
# a = [];self.f(a);print a
return ret
def Find(self, root, target, ret, path):
if not root:
return
path.append(root.val)
isLeaf = (root.left is None and root.right is None)
if isLeaf and target == root.val:
ret.append(path[:]) # Pay attention to this step here,
# If it is: ret.append(path), the result is wrong. Because Python variable objects are all passed by reference.
#print "target:", target, "isLeaf:", isLeaf,
#print "val:", root.val, "path:", path, "ret:", ret
#print
if root.left:
self.Find(root.left, target - root.val, ret, path)
if root.right:
self.Find(root.right, target - root.val, ret, path)
path.pop()
Binary tree image
Title Description
Operate the given binary tree and transform it into a mirror image of the source binary tree.
Enter a description:
Image definition of binary tree: source binary tree
Train of thought:
Swapping left and right subtrees
The idea of recursion is to exchange the positions of the left and right subtrees of the root node first, and then recurse downward, taking the root node of the left and right subtrees as the root node of the next cycle
class Solution:
# Returns the root node of the image tree
def Mirror(self, root):
if root==None:
return
if root.left==None and root.right==None:
return
#These three steps exchange the left and right trees of the root node, the exchanged trees, not just the nodes
tmp=root.right
root.right=root.left
root.left=tmp
if root.left is not None:
self.Mirror(root.left)
if root.right is not None:
self.Mirror(root.right)

