Li Kou's notes have been opened to the public:
Portal
[Author: ArtBoy literature and art

Self-Improvement

There's no better way to overpower a trickle of doubt than with a flood of naked truth.
A flood of facts is the best way to break a trace of doubt.

Title Source:
https://leetcode-cn.com/leetbook/detail/illustration-of-algorithm/

Supporting learning documents:
https://www.kancloud.cn/alex_wsc/dataalg/1853982

Book recommendation:

Comic algorithm

Video recommendation:
https://www.bilibili.com/video/BV1E4411H73v

catalogue

1, Sword finger Offer 12. Path in matrix

Question:

Given an m x n two-dimensional character grid board and a string word word. If word exists in the grid, return true; Otherwise, false is returned.

Words must be formed alphabetically by letters in adjacent cells, where "adjacent" cells are those horizontally or vertically adjacent. Letters in the same cell cannot be reused.

For example, in 3 below × The matrix of 4 contains the word "ABCCED" (the letters in the word are marked).

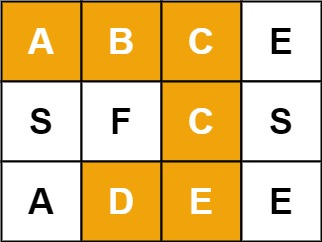
Example 1:

Input: board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
Output: true

Example 2:

Input: board = [["a","b"],["c","d"]], word = "abcd"
Output: false

Tips:

1 <= board.length <= 200
1 <= board[i].length <= 200
board and word It consists of upper and lower case letters only

Solution:

Problem solving idea: DFS + pruning

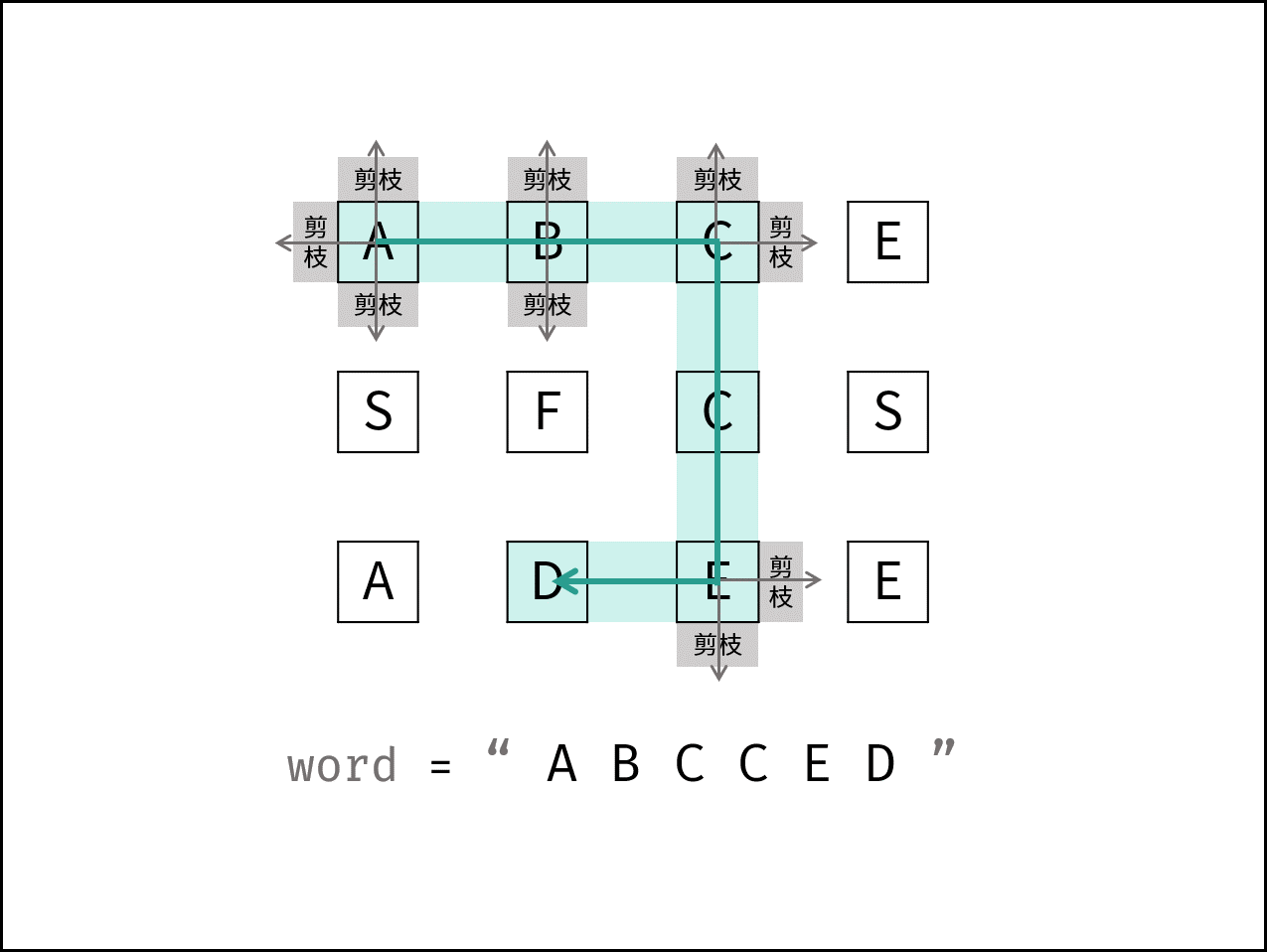
AC Code:

class Solution {
    public boolean exist(char[][] board, String word) {
        char[] words = word.toCharArray();
        for(int i = 0; i < board.length; i++){
            for(int j = 0; j < board[0].length; j++){
                if(dfs(board, words, i, j, 0)) return true;
            }
        }
        return false;
    }
    boolean dfs(char[][] board, char[] words, int i, int j, int k){
        if(i >= board.length || i < 0 || j >= board[0].length || j < 0 || board[i][j] != words[k]) return false; // Subscript out of bounds
        if(k == words.length - 1) return true; // Match all
        board[i][j] = '\0'; // Invalid marker (the next step is to explore the way up, down, left and right. You can't walk through the past, '\ 0' to prevent repetition with the characters in words)
        boolean res = dfs(board, words, i+1, j, k+1) || dfs(board, words, i-1, j, k+1) 
        || dfs(board, words, i, j+1, k+1) || dfs(board, words, i, j-1, k+1); // Up, down, right, left, parallel
        board[i][j] = words[k];
        return res;
    }
}

M. N is the size of matrix rows and columns, and K is the length of string word.

• Time complexity O(3K MN): in the worst case, it is necessary to traverse all schemes with a length of K string in the matrix, and the time complexity is O(3K); There are Mn starting points in the matrix, and the time complexity is O(MN).
• Calculation of the number of schemes: set the length of the string as K, and each character in the search can be selected in the up, down, left and right directions. Discard the back (last character) direction, and there are three options left. Therefore, the complexity of the number of schemes is O(3K).
• Space complexity O(K): the recursion depth in the search process does not exceed K, so the stack space accumulated by the system due to function calls occupies O(K) (because the stack space of system calls will be released after the function returns). In the worst case, K = MN and the recursion depth is Mn. At this time, the system stack uses the additional space of O(MN).

2, 13. Motion range of the robot

Question:

There is a grid of m rows and N columns on the ground, from coordinates [0,0] to coordinates [m-1,n-1]. A robot starts to move from the grid of coordinates [0,0]. It can move left, right, up and down one grid at a time (it cannot move outside the grid), nor can it enter the grid where the sum of digits of row coordinates and column coordinates is greater than k. For example, when k is 18, the robot can enter the grid [35, 37], because 3 + 5 + 3 + 7 = 18. But it cannot enter the grid [35, 38], because 3 + 5 + 3 + 8 = 19. How many grids can the robot reach?

Example 1:

Input: m = 2, n = 3, k = 1
 Output: 3

Example 2:

Input: m = 3, n = 1, k = 0
 Output: 1

Tips:

1 <= n,m <= 100
0 <= k <= 20

Solution:

Problem solving idea: DFS + pruning

Digital sum calculation template:

int sums(int x)
    int s = 0;
    while(x != 0) {
        s += x % 10;  // Get the one digit number of x
        x = x / 10; // Move the decimal number of x one digit to the right, that is, delete one digit.
    }
    return s;

In this problem, the robot can only move one grid at a time, and only the digits and increments from X to x+1 are required for each calculation

(x + 1) % 10 != 0 ? s_x + 1 : s_x - 8;

explain:

• x = 11, x + 1 = 12, digit sum: 2, 3 (2 + 1)
• x = 19, x + 1 = 20, digit sum: 10, 2 (10-8)

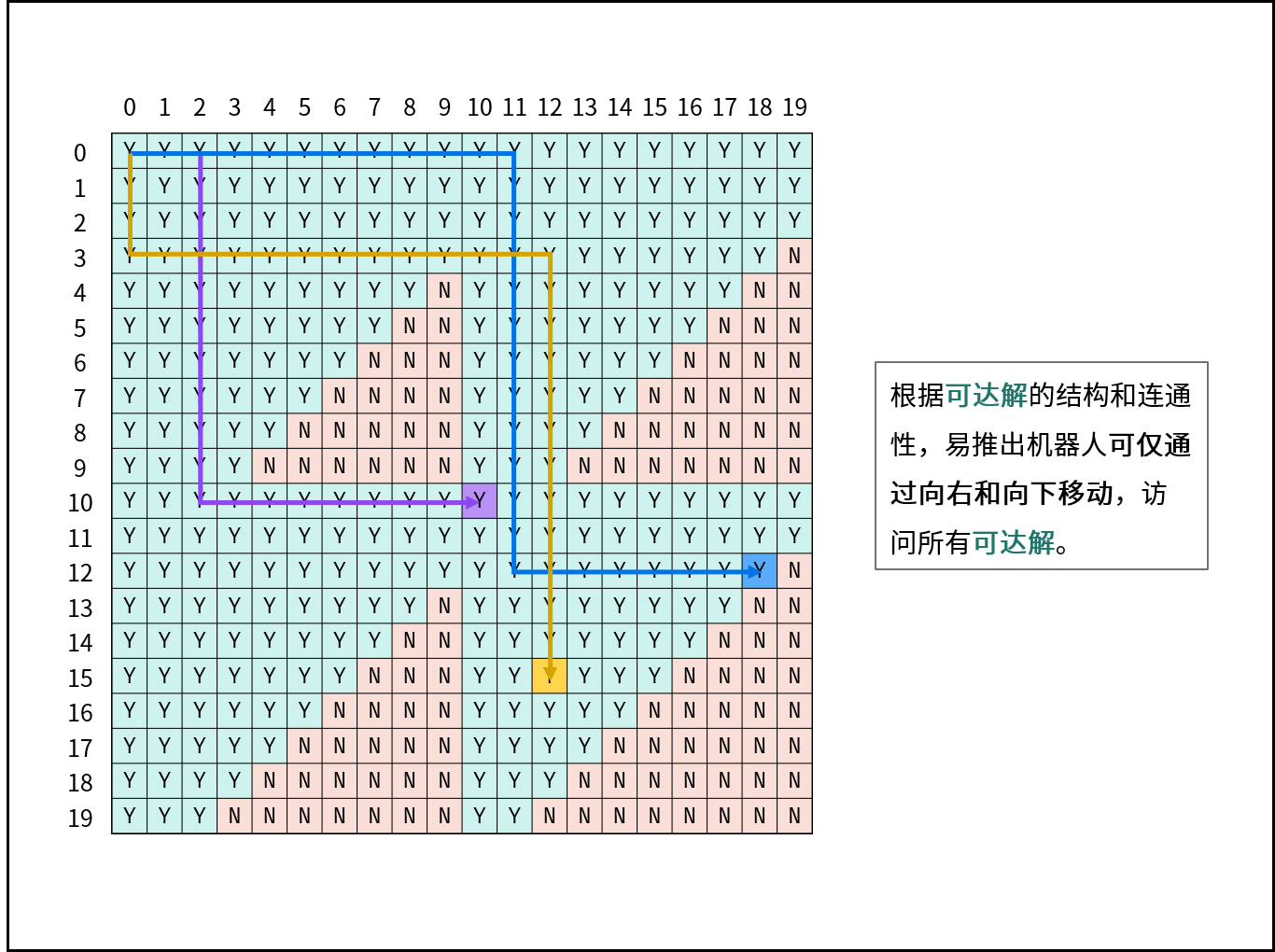
According to the structure and connectivity of reachable solutions, it is easy to deduce that the robot can access all reachable solutions only by moving to the right and down.

AC Code:

class Solution {
    int m, n, k;
    boolean[][] visited;
    public int movingCount(int m, int n, int k) {
        this.m = m; this.n = n; this.k = k;
        this.visited = new boolean[m][n];
        return dfs(0, 0, 0, 0);
    }
    public int dfs(int i, int j, int si, int sj){ // Coordinates, digits and
        if(i >= m || j >= n || si + sj > k || visited[i][j]) return 0; // prune
        visited[i][j] = true; // sign
        int down = dfs(i+1, j, cal(i, si), sj); // Next look
        int right = dfs(i, j+1, si, cal(j, sj)); // Right search
        return 1 + down + right;
    }
    public int cal(int x, int sum){ // Digit and increment
        return (x + 1) % 10 != 0 ? sum + 1 : sum - 8;
    }
}

Problem solving idea: BFS

AC Code:

class Solution {
    public int movingCount(int m, int n, int k) {
        boolean[][] visited = new boolean[m][n];
        int res = 0;
        LinkedList<int[]> queue = new LinkedList<>();
        queue.add(new int[]{0, 0, 0, 0}); // i,j,si,sj
        while(!queue.isEmpty()){
            int[] x = queue.removeFirst();
            int i = x[0], j = x[1], si = x[2], sj = x[3];
            if(i >= m || j >= n || si + sj > k || visited[i][j]) continue;
            visited[i][j] = true;
            res++;
            queue.add(new int[]{i+1, j , cal(i,si), sj});
            queue.add(new int[]{i, j+1, si, cal(j,sj)});
        }
        return res;
    }
    public int cal(int x, int sum){
        return (x + 1)%10 != 0 ? sum + 1 : sum - 8;
    }
}

3, Sword finger Offer 26. Substructure of tree

Question:

Input two binary trees a and B to judge whether B is the substructure of A. (the contract empty tree is not a substructure of any tree)

B is the substructure of A, that is, the same structure and node values as B appear in A.

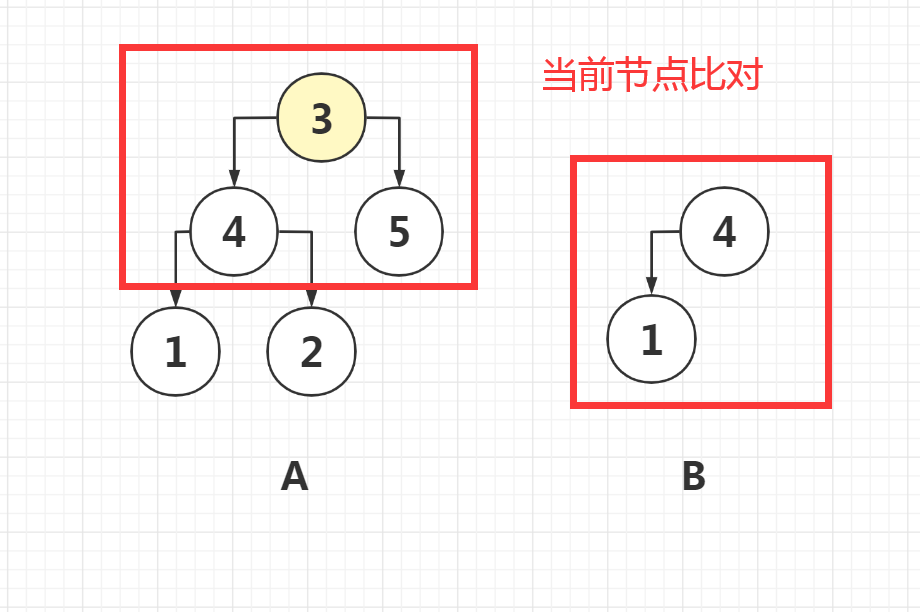
For example:
Given tree A:

     3
    / \
   4   5
  / \
 1   2

Given tree B:

   4 
  /
 1

Returns true because A subtree of B and A has the same structure and node values.

Example 1:

Input: A = [1,2,3], B = [3,1]
Output: false

Example 2:

Input: A = [3,4,5,1,2], B = [4,1]
Output: true

Limitations:

0 <= Number of nodes <= 10000

Solution:

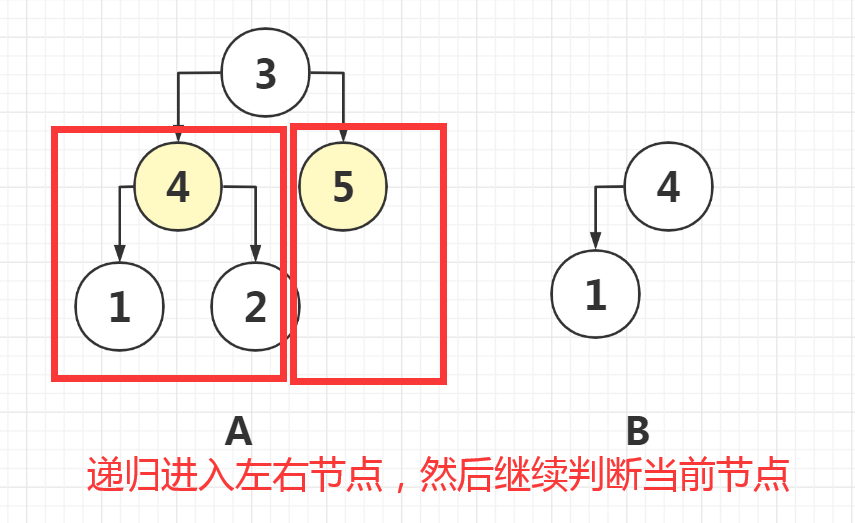
Problem solving idea: first traverse A + judge whether A contains B (double-layer dfs)

AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        // An empty tree is not a substructure of any tree
        if(A == null || B == null) return false;
        // Current node judgment
        if(recur(A,B)) return true;
        // Left and right node judgment
        return isSubStructure(A.left, B) || isSubStructure(A.right, B);
    }
    // Compare current node
    boolean recur(TreeNode A, TreeNode B){
        // B match end
        if(B == null) return true;
        // First judge whether it is null, and then judge whether its val is equal, otherwise a null pointer exception will be reported
        if(A == null || A.val != B.val) return false;
        return recur(A.left, B.left) && recur(A.right, B.right);
    }
}

• Time complexity O(MN): where m and N are the number of nodes of tree A and tree B respectively; First traverse the tree a to occupy O(M), and each time call recur(A, B) to judge the occupation of O(N).
• Spatial complexity O(M): when both tree A and tree B degenerate into linked lists, the recursive call depth is the largest. When M ≤ n, the total recursive depth of traversing tree A and recursive judgment is M; When M > N, the worst case is to traverse to the leaf node of tree a, and the total recursion depth is M.

4, Sword finger Offer 27. Image of binary tree

Question:

Please complete a function, input a binary tree, and the function outputs its image.

For example, enter:

     4
   /   \
  2     7
 / \   / \
1   3 6   9

Mirror output:

     4
   /   \
  7     2
 / \   / \
9   6 3   1

Example 1:

Input: root = [4,2,7,1,3,6,9]
Output:[4,7,2,9,6,3,1]

Limitations:

0 <= Number of nodes <= 1000

Solution:

Problem solving idea: recursion
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        // It must be judged as null before taking value to prevent null exception
        if(root == null) return null;
        TreeNode temp = root.left;
        // Right flip left
        root.left = mirrorTree(root.right);
        // temp flip right
        root.right = mirrorTree(temp);
        return root;
    }
}

• Time complexity O(N): where N is the number of nodes of the binary tree. To establish a binary tree image, you need to traverse all nodes of the tree, taking O(N) time.
• Space complexity O(N): in the worst case (when the binary tree degenerates into a linked list), the system needs to use stack space of O(N) size for recursion.

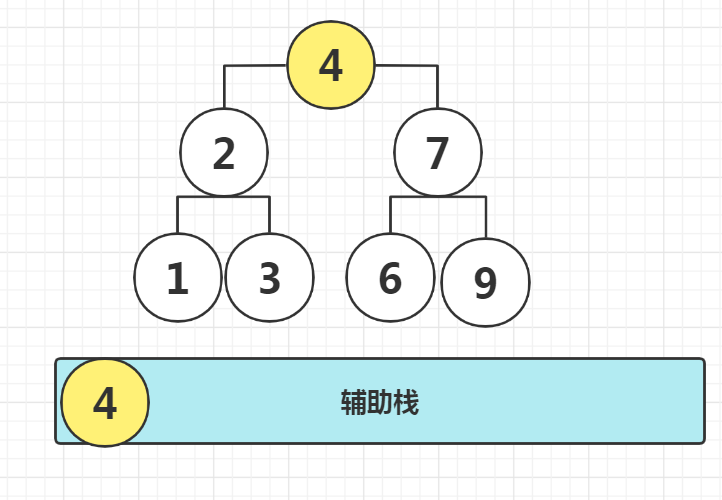
Solution idea: auxiliary stack traversal exchange

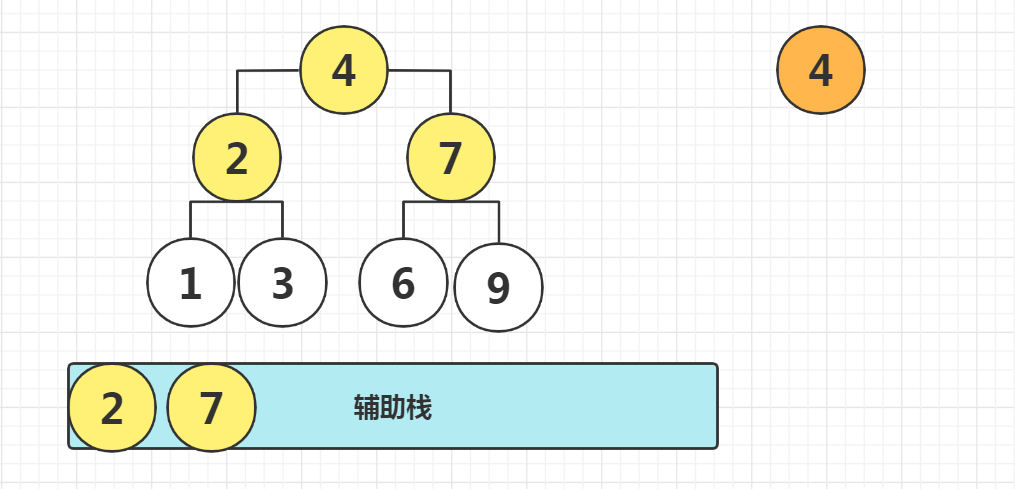
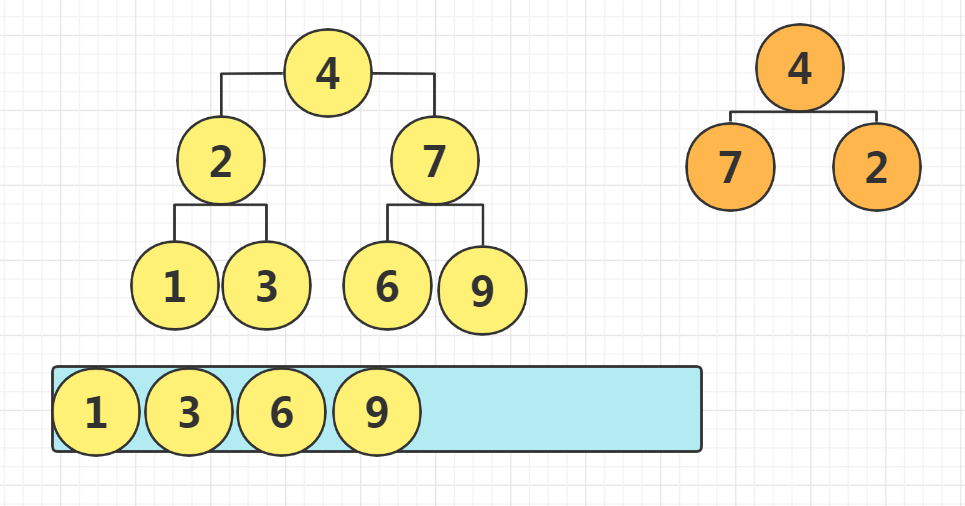
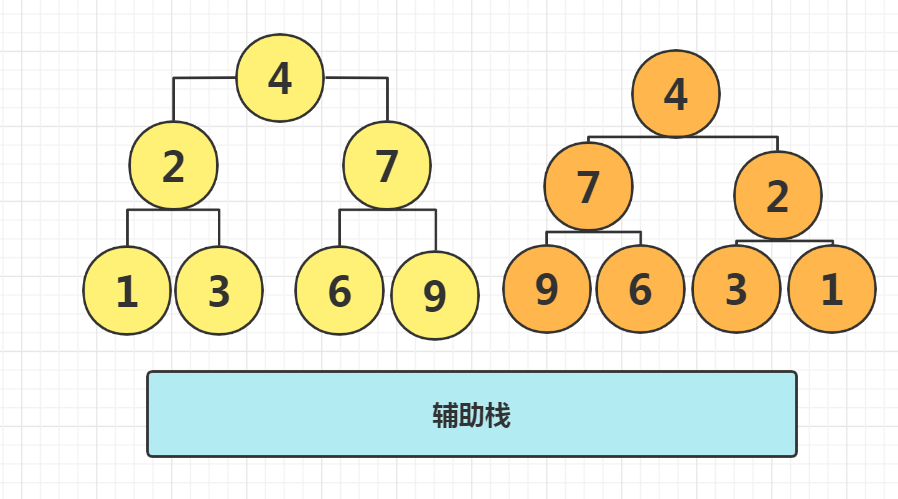
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;
        // Traverse the whole tree through the stack (store the nodes to be accessed and pop up the accessed nodes)
        LinkedList<TreeNode> stack = new LinkedList<>(){{add(root);}};
        while(!stack.isEmpty()){
            // Pop up the node being accessed
            TreeNode node = stack.removeLast();
            // Record the left and right nodes for the next visit
            if(node.left != null) stack.add(node.left);
            if(node.right != null) stack.add(node.right);
            // exchange
            TreeNode temp = node.left;
            node.left = node.right;
            node.right = temp;
        }
        return root;
    }
}

• Time complexity O(N): where N is the number of nodes of the binary tree. To establish a binary tree image, you need to traverse all nodes of the tree, taking O(N) time.
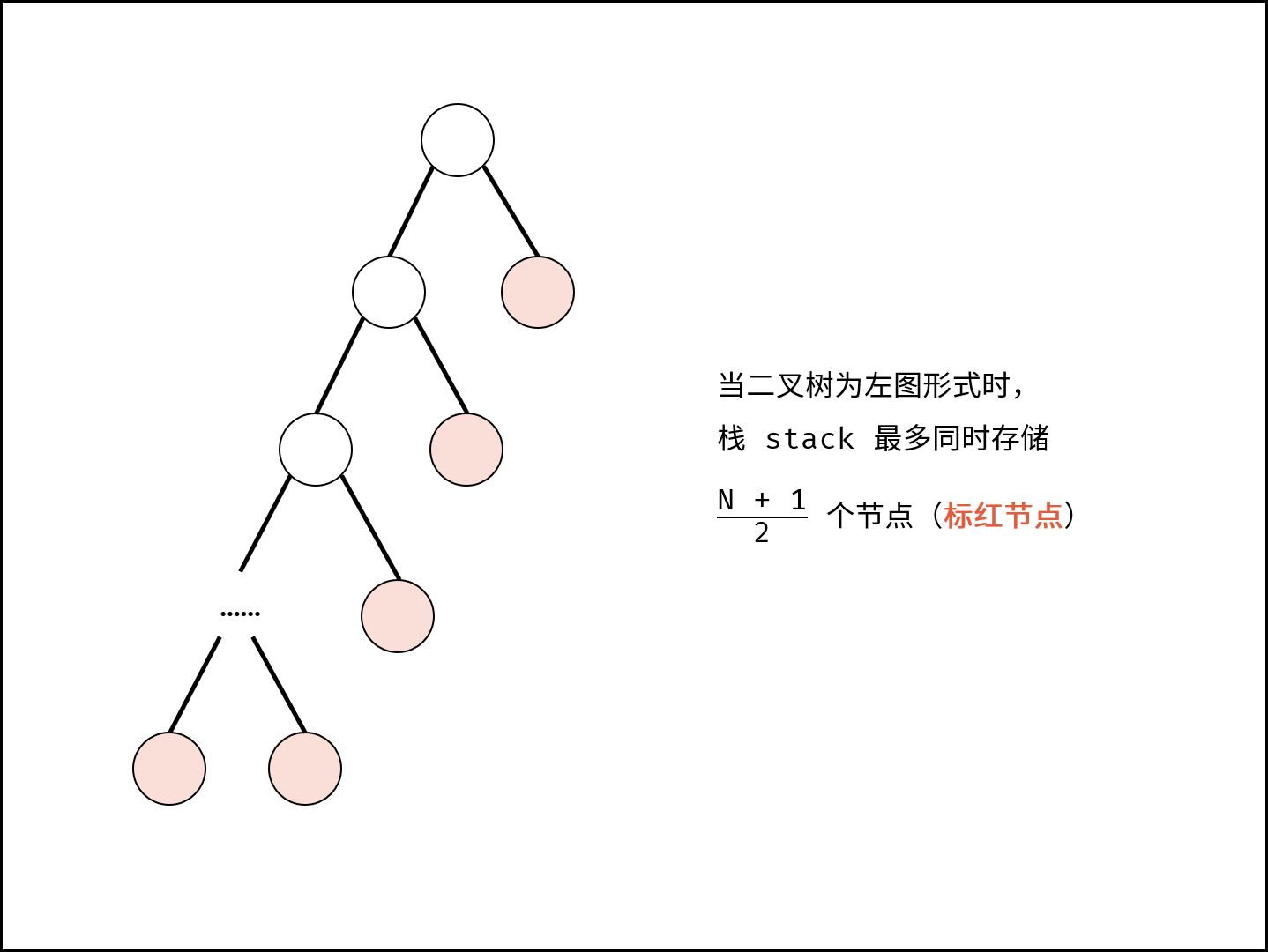
• Space complexity O(N): as shown in the figure below, in the worst case, stack stack can be stored at most at the same time N + 1 2 \frac{N+1}{2} 2N+1} nodes, occupying O(N) additional space.
  

5, Sword finger Offer 28. Symmetric binary tree

Question:

Please implement a function to judge whether a binary tree is symmetrical. If a binary tree is the same as its mirror, it is symmetrical.

For example, a binary tree [1,2,2,3,4,4,3] is symmetric.

    1
   / \
  2   2
 / \ / \
3  4 4  3

However, the following [1,2,2,null,3,null,3] is not mirror symmetric:

    1
   / \
  2   2
   \   \
   3    3

Example 1:

Input: root = [1,2,2,3,4,4,3]
Output: true

Example 2:

Input: root = [1,2,2,null,3,null,3]
Output: false

Limitations:

0 <= Number of nodes <= 1000

Solution:

Solution idea: recursive traversal and comparison one by one
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null) return true;
        return recur(root.left, root.right);
    }
    boolean recur(TreeNode L, TreeNode R){
        // 50. R ends recursively at the same time
        if(L == null && R == null) return true;
        // L or R has an early end, with different values
        if(L == null || R == null || L.val != R.val) return false;
        return recur(L.left, R.right) && recur(L.right, R.left);
    }
}

• Time complexity O(N): where N is the number of nodes in the binary tree. Each execution of recur() can judge whether a pair of nodes are symmetrical. Therefore, the recur() method can be called N/2 times at most.
• Spatial complexity O(N): as shown in the figure below, in the worst case (binary tree degenerates into linked list), the system uses a space of O(N).

6, Sword finger Offer 32 - I. print binary tree from top to bottom

Question:

Each node of the binary tree is printed from top to bottom, and the nodes of the same layer are printed from left to right.

For example:
Given binary tree: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

return:

[3,9,20,15,7]

Tips:

Total number of nodes <= 1000

Solution:

Problem solving idea: BFS
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int[] levelOrder(TreeNode root) {
        if(root == null) return new int[0];
        List<Integer> res = new ArrayList<>();
        // BFS template
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            TreeNode node = queue.removeFirst();
            res.add(node.val);
            if(node.left != null) queue.add(node.left);
            if(node.right != null) queue.add(node.right);
        }
        // List to array
        int[] ans = new int[res.size()];
        for(int i = 0; i < res.size(); i++){
            ans[i] = res.get(i);
        }
        return ans;
    }
}

• Time complexity O(N): N is the number of nodes in the binary tree, that is, BFS needs to cycle N times.
• Spatial complexity O(N): in the worst case, that is, when the tree is a balanced binary tree, there are at most N/2 tree nodes in the queue at the same time, and the additional space of O(N) size is used.

7, Sword finger Offer 32 - II. Print binary tree II from top to bottom

Question:

The binary tree is printed by layers from top to bottom, the nodes of the same layer are printed from left to right, and each layer is printed to one line.

For example:
Given binary tree: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

Return its hierarchy traversal result:

[
  [3],
  [9,20],
  [15,7]
]

Tips:

Total number of nodes <= 1000

Solution:

Problem solving idea: BFS
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> temp = new ArrayList<>();
            // Sequence traversal and output
            int num = queue.size(); // Get the number of nodes in this layer
            while((num --) > 0){
                TreeNode node = queue.removeFirst();
                temp.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);
            }
            res.add(temp);
        }
        return res;
    }
}

8, Sword finger Offer 32 - III. print binary tree III from top to bottom

Question:

Please implement a function to print the binary tree in zigzag order, that is, the first line is printed from left to right, the second layer is printed from right to left, the third line is printed from left to right, and so on.

For example:
Given binary tree: [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

Return its hierarchy traversal result:

[
  [3],
  [20,9],
  [15,7]
]

Tips:

Total number of nodes <= 1000

Solution:

Solution: sequence traversal + double ended queue
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            LinkedList<Integer> temp = new LinkedList<>();
            int num = queue.size(); // level traversal 
            while((num --) > 0){
                TreeNode node = queue.removeFirst();
                if(res.size() % 2 == 0){ // The initial length is 0
                    temp.add(node.val);
                }else{
                    temp.addFirst(node.val);
                }
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);          
            }
            res.add(temp);
        }
        return res;       
    }
}

Problem solving ideas:
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if(root == null) return res;
        LinkedList<TreeNode> queue = new LinkedList<>();
        queue.add(root);
        while(!queue.isEmpty()){
            List<Integer> temp = new ArrayList<>();
            int num = queue.size(); // level traversal 
            while((num --) > 0){
                TreeNode node = queue.removeFirst();
                temp.add(node.val);
                if(node.left != null) queue.add(node.left);
                if(node.right != null) queue.add(node.right);          
            }
            if(res.size()%2 != 0) Collections.reverse(temp);
            res.add(temp);
        }
        return res;       
    }
}

9, Sword finger Offer 34. A path with a certain value in a binary tree

Question:

Enter a binary tree and an integer, and print out all paths where the sum of node values in the binary tree is the input integer. A path is formed from the root node of the tree down to the leaf node.

A leaf node is a node that has no children.

Example:
Given the following binary tree, and target and target = 22,

          5
         / \
        4   8
       /   / \
      11  13  4
     /  \    / \
    7    2  5   1

return:

[
   [5,4,11,2],
   [5,8,4,5]
]

Tips:

Total number of nodes <= 10000

Solution:

Solution idea: first order traversal + path record
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    LinkedList<List<Integer>> res = new LinkedList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> pathSum(TreeNode root, int target) {
        dfs(root, target);
        return res;
    }
    void dfs(TreeNode root, int tar){
        if(root == null) return;
        path.add(root.val);
        tar -= root.val;
        if(tar == 0 && root.left == null && root.right == null){
            res.add(new LinkedList(path));
        }
        dfs(root.left, tar);
        dfs(root.right, tar);
        path.removeLast();
    }
}

10, Sword finger Offer 36. Binary search tree and bidirectional linked list

Question:

Enter a binary search tree and convert the binary search tree into a sorted circular two-way linked list. It is required that no new node can be created, and only the node pointer in the tree can be adjusted.
To better understand the problem, take the following binary search tree as an example:

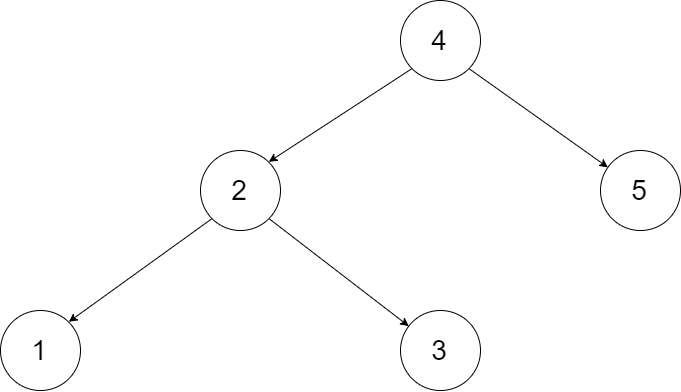
We hope to transform this binary search tree into a two-way circular linked list. Each node in the linked list has a precursor and successor pointer. For a two-way circular linked list, the precursor of the first node is the last node, and the successor of the last node is the first node.

The following figure shows the linked list transformed from the above binary search tree. "head" refers to the node with the smallest element in the linked list.

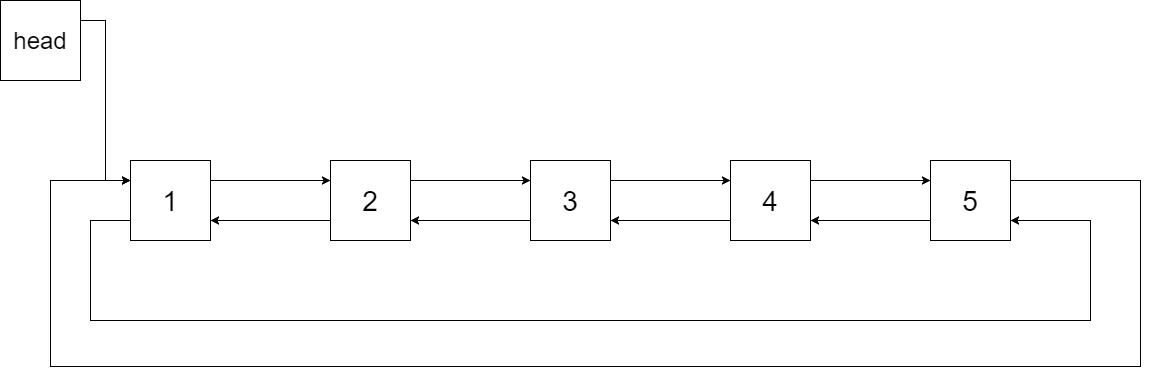
In particular, we want the conversion to be done in place. After the conversion is completed, the left pointer of the node in the tree needs to point to the precursor and the right pointer of the node in the tree needs to point to the successor. You also need to return the pointer of the first node in the linked list.

Solution:

Solution idea: middle order traversal + two-way linked list + circular linked list

It is worth noting that the middle order traversal of the binary search tree in this problem can realize the increasing sequence

AC Code:

/*
// Definition for a Node.
class Node {
    public int val;
    public Node left;
    public Node right;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val,Node _left,Node _right) {
        val = _val;
        left = _left;
        right = _right;
    }
};
*/
class Solution {
    Node pre,head;
    public Node treeToDoublyList(Node root) {
        if(root == null) return null;
        dfs(root);
        // Head to tail docking
        head.left = pre;
        pre.right = head;
        return head;
    }
     void dfs(Node cur){
        if(cur == null) return;
        // Medium order traversal
        dfs(cur.left); // Left
        // root
        // Double linked list template
        if(pre != null) pre.right = cur;
        else head = cur;
        cur.left = pre;
        // Pointer pre shift right
        pre = cur;
        dfs(cur.right); // right
    }
}

• Time complexity O(N): N is the number of nodes of the binary tree, and all nodes need to be accessed for medium order traversal.
• Space complexity O(N): in the worst case, that is, when the tree degenerates into a linked list, the recursion depth reaches N, and the system uses O(N) stack space.

11, Sword finger Offer 37. Serialized binary tree

Question:

Please implement two functions to serialize and deserialize the binary tree respectively.

You need to design an algorithm to realize the serialization and deserialization of binary tree. There is no restriction on the execution logic of your sequence / deserialization algorithm. You only need to ensure that a binary tree can be serialized into a string and deserialize the string into the original tree structure.

Note: the input / output format is the same as that currently used by LeetCode. For details, please refer to the format of LeetCode serialized binary tree. You don't have to take this approach, you can also take other methods to solve the problem.

Example:

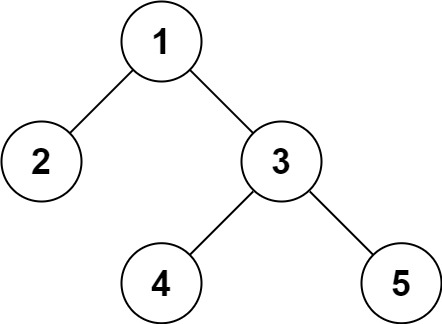
Input: root = [1,2,3,null,null,4,5]
Output:[1,2,3,null,null,4,5]

Solution:

Solution: sequence traversal
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Codec {

    // Encodes a tree to a single string.
    public String serialize(TreeNode root) {
        if(root == null) return "[]";
        StringBuilder res = new StringBuilder("[");
        // BFS
        LinkedList<TreeNode> queue = new LinkedList<>(){{add(root);}};
        while(!queue.isEmpty()){
            TreeNode node = queue.removeFirst();
            if(node != null){
                res.append(node.val + ",");
                queue.add(node.left);
                queue.add(node.right);
            }else res.append("null,");
        }
        res.deleteCharAt(res.length() - 1); // Remove the last comma
        res.append("]");
        return res.toString();
    }

    // Decodes your encoded data to tree.
    public TreeNode deserialize(String data) {
        if(data.equals("[]")) return null;
        // string manipulation
        String[] vals = data.substring(1, data.length() - 1).split(",");
        // BFS
        int index = 0; // Traversal array pointer
        TreeNode root = new TreeNode(Integer.parseInt(vals[index++]));
        LinkedList<TreeNode> queue = new LinkedList<>(){{add(root);}};
        while(!queue.isEmpty()){
            TreeNode node = queue.removeFirst();
            if(!vals[index].equals("null")){
                node.left = new TreeNode(Integer.parseInt(vals[index]));
                queue.add(node.left);
            }
            index ++;
            if(!vals[index].equals("null")){
                node.right = new TreeNode(Integer.parseInt(vals[index]));
                queue.add(node.right);
            }
            index ++;
        }
        return root;
    }
}

// Your Codec object will be instantiated and called as such:
// Codec codec = new Codec();
// codec.deserialize(codec.serialize(root));

• Time complexity O(N): N is the number of nodes of the binary tree. Sequence traversal needs to access all nodes. In the worst case, it needs to access N + 1 null s. The overall complexity is
  O( N + 1 2 \frac{N+1}{2} 2N+1​) = O(N).
• Spatial complexity O(N): in the worst case, the queue stores 2N+1 nodes (or N+1 null s) at the same time, using O(N); The list res uses O(N).

12, Sword finger Offer 38. Arrangement of strings

Question:

Enter a string and print out all the arrangements of characters in the string.

You can return this string array in any order, but there can be no duplicate elements.

Example:

Input: s = "abc"
Output:["abc","acb","bac","bca","cab","cba"]

Limitations:

1 <= s Length of <= 8

Solution:

Problem solving ideas: dfs + backtracking
Illustration:

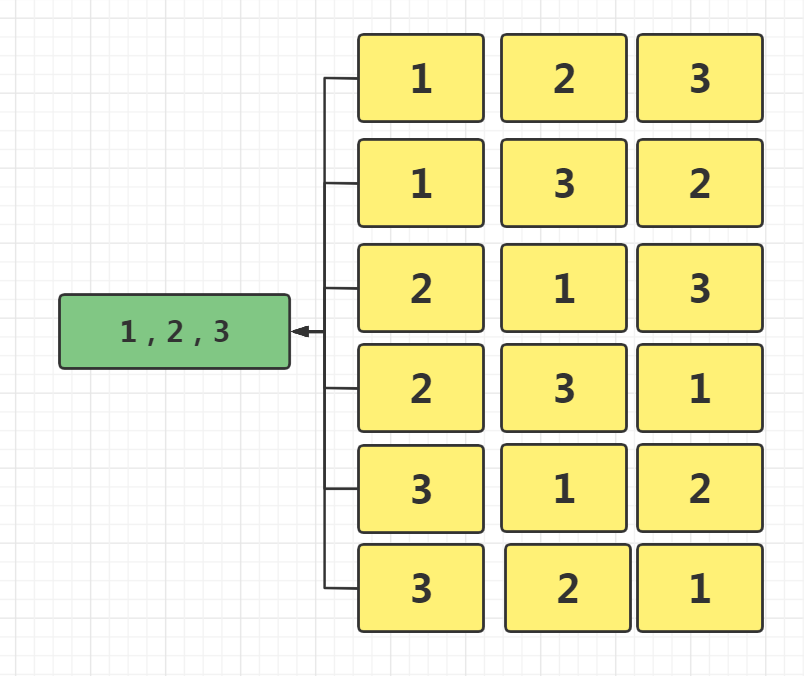
List all full permutations of 1, 2 and 3, and add dfs traversal to res one by one

For a string of length n (assuming that the characters do not repeat each other), the number of arrangement schemes is: n × (n−1) × (n−2)… × two × one

swap() function:

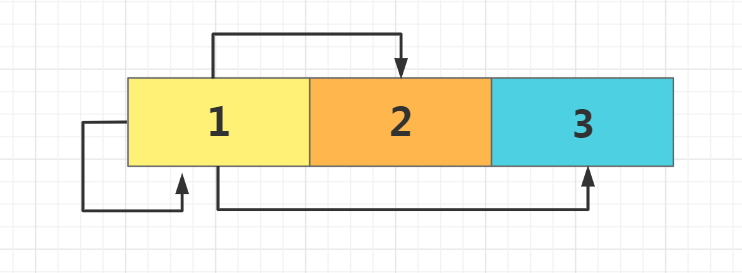
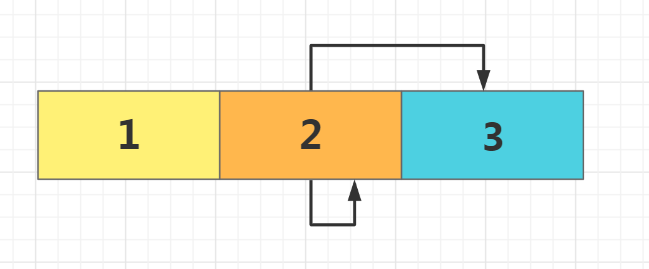
AC Code:

class Solution {
    List<String> res = new LinkedList<>();
    char[] c;
    public String[] permutation(String s) {
        c = s.toCharArray();
        dfs(0);
        return res.toArray(new String[res.size()]);
    }
    void dfs(int x) {
        if(x == c.length - 1) {
            res.add(String.valueOf(c));      // Add arrangement scheme
            return;
        }
        HashSet<Character> set = new HashSet<>();
        for(int i = x; i < c.length; i++) {
            if(set.contains(c[i])) continue; // Repeat, so prune
            set.add(c[i]);
            swap(i, x);                      // Swap, fix c[i] in bit x
            dfs(x + 1);                      // Turn on fixed x + 1 st character
            swap(i, x);                      // Recovery exchange
        }
    }
    void swap(int a, int b) {
        char tmp = c[a];
        c[a] = c[b];
        c[b] = tmp;
    }
}

• Time complexity O(N!N): n is the length of string s; The time complexity is linear with the number of schemes of string arrangement, and the number of schemes is n × (N−1) × (N−2)… × two × 1, that is, the complexity is O(N!); The string splicing operation join() uses O(N); Therefore, the overall time complexity is O(N!N).
• Space complexity O(N2): the recursion depth of full permutation is n, and the cumulative stack space used by the system is O(N); The maximum cumulative number of characters stored by the auxiliary Set in recursion is N + (N-1) +... + 2 + 1 = (N+1)N/2, that is, it occupies additional space of O(N2).

13, Sword finger Offer 54. The k-th node of the binary search tree

Question:

Given a binary search tree, please find the k-largest node.

Example 1:

input: root = [3,1,4,null,2], k = 1
   3
  / \
 1   4
  \
   2
 output: 4

Example 2:

input: root = [5,3,6,2,4,null,null,1], k = 3
       5
      / \
     3   6
    / \
   2   4
  /
 1
 output: 4

Limitations:

1 ≤ k ≤ Number of binary search tree elements

Solution:

Solution idea: middle order traversal reverse order
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    int res, k; // Returned result, k
    public int kthLargest(TreeNode root, int k) {
		this.k = k;
        dfs(root); // Inverse middle order traversal
        return res;
    }
    void dfs(TreeNode root){
		if(root == null) return;
        dfs(root.right); // right
        k--;
        if(k == 0){
			res = root.val;
            return;
        }
        dfs(root.left); // Left
    }
}

• Time complexity O(N): when the tree degenerates into a linked list (all right child nodes), the recursion depth is N regardless of the value of k, occupying O(N) time.
• Space complexity O(N): when the tree degenerates into a linked list (all right child nodes), the system uses a stack space of O(N).

14, Sword finger Offer 55 - I. depth of binary tree

Question:

Enter the root node of a binary tree to find the depth of the tree. The nodes (including root and leaf nodes) passing from root node to leaf node form a path of the tree, and the length of the longest path is the depth of the tree.

For example:

Given binary tree [3,9,20,null,null,15,7],

    3
   / \
  9  20
    /  \
   15   7

Returns its maximum depth 3.

Tips:

Total number of nodes <= 10000

Solution:

Problem solving idea: DFS (post order traversal)
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0; // Export
        return Math.max(maxDepth(root.left),maxDepth(root.right)) + 1;
    }
}

• Time complexity O(N): N is the number of nodes in the tree. To calculate the depth of the tree, you need to traverse all nodes.
• Spatial complexity O(N): in the worst case (when the tree degenerates into a linked list), the recursion depth can reach N.

Problem solving idea: BFS
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null) return 0;
        LinkedList<TreeNode> queue = new LinkedList<>(){{add(root);}};
        int res = 0;
        while(!queue.isEmpty()){
            LinkedList<TreeNode> temp = new LinkedList<>();
            // level traversal 
            for(TreeNode node : queue){
                if(node.left != null) temp.add(node.left);
                if(node.right != null) temp.add(node.right);
            }
            queue = temp;
            res ++;
        }
        return res;
    }
}

• Time complexity O(N): N is the number of nodes in the tree. To calculate the depth of the tree, you need to traverse all nodes.
• Spatial complexity O(N): in the worst case (when the tree is balanced), the queue stores N/2 nodes at the same time.

15, Sword finger Offer 55 - II. Balanced binary tree

Question:

Enter the root node of a binary tree to judge whether the tree is a balanced binary tree. If the depth difference between the left and right subtrees of any node in a binary tree is no more than 1, it is a balanced binary tree.

Example 1:

Given binary tree [3,9,20,null,null,15,7]

    3
   / \
  9  20
    /  \
   15   7

Returns true.

Example 2:

Given binary tree [1,2,2,3,3,null,null,4,4]

       1
      / \
     2   2
    / \
   3   3
  / \
 4   4

Returns false.

Limitations:

0 <= Number of nodes in the tree <= 10000

Solution:

Problem solving idea: first order traversal + judgment depth (from top to bottom)
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if(root == null) return true;
        return Math.abs(dfs(root.left) - dfs(root.right)) <= 1 && isBalanced(root.left) && isBalanced(root.right);
    }
    // Returns the depth of the node
    int dfs(TreeNode root){
        if(root == null) return 0;
        return Math.max(dfs(root.left), dfs(root.right)) + 1;
    }
}

16, Sword finger Offer 64. Find 1 + 2 +... + n

Question:

For 1 + 2 +... + n, it is required that keywords such as multiplication and division, for, while, if, else, switch, case and conditional judgment statements (A?B:C) cannot be used.

Example 1:

input: n = 3
 output: 6

Example 2:

input: n = 9
 output: 45

Limitations:

1 <= n <= 10000

Solution:

Solution idea: bit operation
AC Code:

class Solution {
    int res = 0;
    public int sumNums(int n) {
        boolean x = n > 1 && sumNums(n-1) > 0;
        res += n;
        return res;
    }
}

17, Sword finger Offer 68 - I. nearest common ancestor of binary search tree

Question:

Given a binary search tree, find the nearest common ancestor of two specified nodes in the tree.

Baidu Encyclopedia defines the nearest public ancestor as: "for two nodes p and q with root tree T, the nearest public ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q, and the depth of X is as large as possible (a node can also be its own ancestor)."

For example, give the following binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

Example 1:

input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
 output: 6 
explain: The nearest common ancestor of node 2 and node 8 is 6.

Example 2:

input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
 output: 2
 explain: The nearest common ancestor of node 2 and node 4 is 2, Because according to the definition, the nearest common ancestor node can be the node itself.

explain:

The values of all nodes are unique.
p,q Are different nodes and all exist in a given binary search tree.

Solution:

Problem solving idea: recursion

Binary lookup tree: unique value, left less than right

Definition of ancestor: if node p is in the left (right) subtree of node root, or p = root, root is said to be the ancestor of p.

Nearest common ancestor: set node root as a common ancestor of nodes P and Q. if its left child node root.left and right child node root.right are not the common ancestors of P and Q, root is called "nearest common ancestor".

AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        // On the right side of the root node
        if(root.val < p.val && root.val < q.val) return lowestCommonAncestor(root.right,p,q);
        // To the left of the root node
        if(root.val > p.val && root.val > q.val) return lowestCommonAncestor(root.left,p,q);
        // Different side
        return root;
    }
}

• Time complexity O(N): where N is the number of binary tree nodes; One layer is excluded in each cycle. The minimum number of layers of binary search tree is logN (full binary tree) and the maximum is N (degenerated into linked list).
• Spatial complexity O(N): in the worst case, that is, when the tree degenerates into a linked list, the recursion depth reaches the number of layers N of the tree.

18, Sword finger Offer 68 - II. Nearest common ancestor of binary tree

Question:

Given a binary tree, find the nearest common ancestor of two specified nodes in the tree.

Baidu Encyclopedia defines the nearest public ancestor as: "for two nodes p and q with root tree T, the nearest public ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q, and the depth of X is as large as possible (a node can also be its own ancestor)."

For example, give the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]

Example 1:

input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
 output: 3
 explain: The nearest common ancestor of node 5 and node 1 is node 3.

Example 2:

input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
 output: 5
 explain: The nearest common ancestor of node 5 and node 4 is node 5. Because according to the definition, the nearest common ancestor node can be the node itself.

explain:

The values of all nodes are unique.
p,q Are different nodes and all exist in a given binary tree.

Solution:

Problem solving ideas:
AC Code:

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root == null || root == p || root == q) return root; // Export
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if(left != null && right != null) return root; // There are both left and right subtrees
        else return left != null ? left : right;
    }
}