[sword finger Offer] search and backtracking algorithm

Sword finger Offer 64. Find 1 + 2 +... + n

For 1+2+...+n, it is required that keywords such as multiplication and division, for, while, if, else, switch, case and conditional judgment statements (A?B:C) cannot be used.

Example 1:

input: n = 3
 output: 6

Example 2:

input: n = 9
 output: 45

class Solution {
public:
    int sumNums(int n) {
        int ans = 0;
        n != 0 && (ans = sumNums(n - 1) + n);
        return ans;
    }
};

Algorithm idea

This problem can be solved by recursion, but considering that the recursion exit needs to be judged but not if, the solution here is to use the short-circuit operation of logic and, that is, when the first half of the statement is false, the second half of the statement is not executed, which forms the judgment of a recursion exit.

Limitations:

1 <= n <= 10000

Sword finger Offer 68 - I. nearest common ancestor of binary search tree

Given a binary search tree, find the nearest common ancestor of two specified nodes in the tree.

Baidu Encyclopedia The definition of nearest common ancestor in is: "for two nodes p and q with root tree T, the nearest common ancestor is expressed as a node x, which satisfies that x is the ancestor of p and q and the depth of X is as large as possible (a node can also be its own ancestor)."

For example, give the following binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]

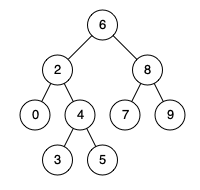
Example 1:

input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
 output: 6 
explain: The nearest common ancestor of node 2 and node 8 is 6.

Example 2:

input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
 output: 2
 explain: The nearest common ancestor of node 2 and node 4 is 2, Because according to the definition, the nearest common ancestor node can be the node itself.

explain:

The values of all nodes are unique.
p. q is different nodes and exists in a given binary search tree.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == nullptr || root == p || root == q){
            return root;
        }
        TreeNode* l = lowestCommonAncestor(root->left, p, q);
        TreeNode* r = lowestCommonAncestor(root->right, p, q);
        return l == nullptr? r : (r == nullptr ? l : root);
    }
};

Algorithm idea

To judge whether a point is the first common priority of two nodes, one feature is that the two nodes are in two subtrees respectively, and the two target nodes are not other ancestor nodes of the first ancestor node. In fact, the two target nodes are only distributed in one subtree, so you can traverse from top to bottom. In the process of backtracking, you can judge whether the first ancestor node can get the answer.

Sword finger Offer 68 - II. Nearest common ancestor of binary tree

Given a binary tree, find the nearest common ancestor of two specified nodes in the tree.

For example, give the following binary tree: root = [3,5,1,6,2,0,8,null,null,7,4]

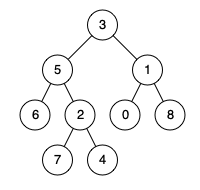
Example 1:

input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
 output: 3
 explain: The nearest common ancestor of node 5 and node 1 is node 3.

Example 2:

input: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
 output: 5
 explain: The nearest common ancestor of node 5 and node 4 is node 5. Because according to the definition, the nearest common ancestor node can be the node itself.

explain:

The values of all nodes are unique.
p. q is different nodes and exists in a given binary tree.

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    unordered_map<TreeNode*, int> lev;
    unordered_map<TreeNode*, map<int, TreeNode*>> st;
    void dfs(TreeNode *root, TreeNode *pre){
        if(root == nullptr)return;
        lev[root] = lev[pre] + 1;
        st[root][0] = pre;
        for(int i = 1; i < 50; ++ i){
            st[root][i] = st[st[root][i - 1]][i - 1];
        }
        dfs(root->left, root);
        dfs(root->right, root);
    }
    TreeNode* lca(TreeNode *p, TreeNode *q){
        if(lev[p] < lev[q]){
            swap(p, q);
        }
        while(lev[p] > lev[q]){
            p = st[p][(int)log2(lev[p] - lev[q])];
        }
        if(p == q){
            return p;
        }
        for(int i = 49; i >= 0; -- i){
            if(st[p][i] != st[q][i]){
                p = st[p][i];
                q = st[q][i];
            }
        }
        return st[p][0];
    }
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        dfs(root, nullptr);
        return lca(p, q);
    }
};

Algorithm idea

This problem seems to be the same as the second problem, but I measured it. It seems that the data scale is different. This problem has a large scale. The above solution is the best way to solve this problem, but I used a special algorithm "multiplication" in the third one. For example, if you want to go to a place of 28 meters, you can walk 1 meter, 2 meters, 3 meters... 28 meters until 28 meters, but in fact, you only need to walk 1 meter, 2 meters, 4 meters, 8 meters and 16 meters to reach 28. For example, numbers within 27 = 16 + 8 + 2 + 1, 21 = 16 + 4 + 1... 28 can be composed of the five numbers in front of you (1,2,4,8,16). In this problem, for two nodes, we can first let the low-level node go up until the two nodes are on the same level. If the times of two nodes are the same, then the node is the result; Otherwise, the two nodes go up at the same time until they meet for the first time, which is the result. How to go up and the number of steps you take are multiplied. The code is still troublesome, and it is not the optimal method (or even poor). The main thing is to understand the multiplication algorithm, which is still very efficient for other problems.

Posted by dcav on Sun, 26 Sep 2021 20:11:35 -0700

Programmer Group

[sword finger Offer] search and backtracking algorithm

Sword finger Offer 64. Find 1 + 2 +... + n

Sword finger Offer 68 - I. nearest common ancestor of binary search tree

Sword finger Offer 68 - II. Nearest common ancestor of binary tree

Hot Keywords