Ru and De Solution:

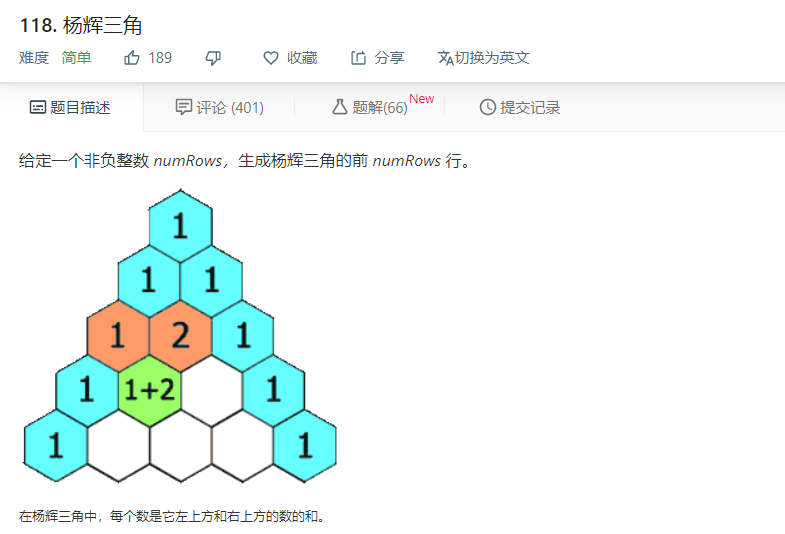
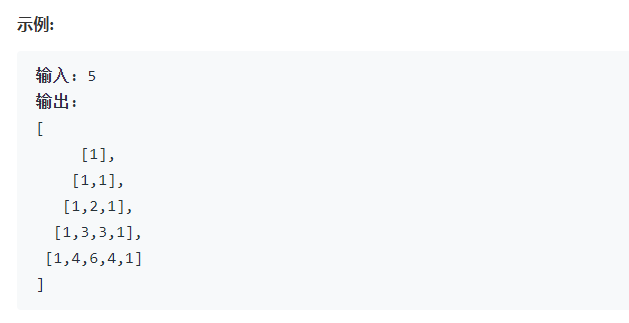
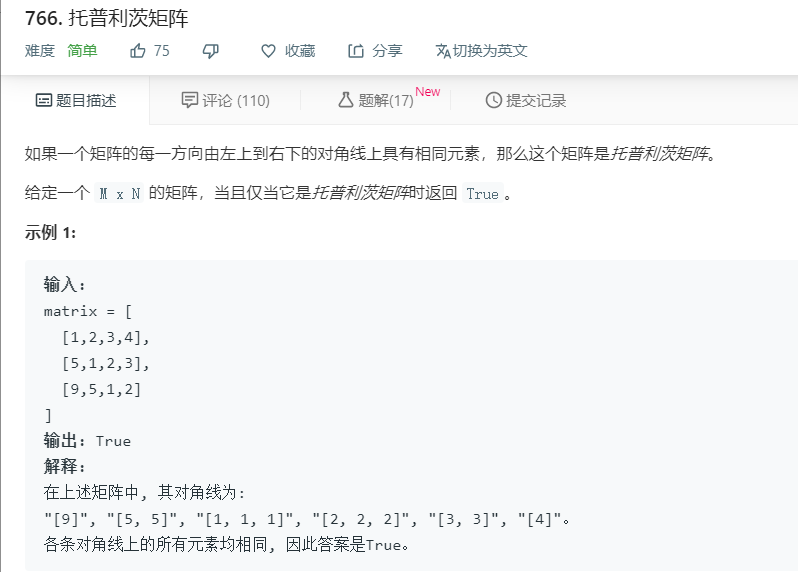
1. Solving the problem: For Yang Hui triangle, it can be converted to a right triangle type.

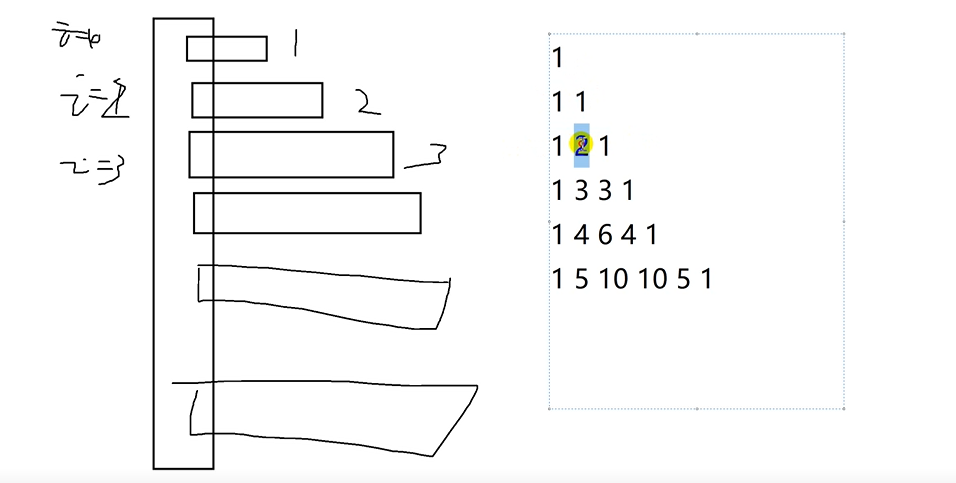
With the increase of each row, the columns of each row also change with the number of rows. At the beginning and end of each row, they are all 1. Look at Yang Hui triangle. Change. Starting from three rows, except from the beginning and the end, the number of the middle changes with the two above rows. With the increase of the number, the number of the middle corresponds with the number of the previous row. Number (one in the same profession plus one in the same nurse profession).

import java.util.ArrayList;
import java.util.List;

public List<List<Integer>> generate(int numRows){

    List<List<Integer>> lists = new ArrayList<List<Integer>>();
    
    for( int i = 1 ; i <= numRows ; i++){
        ArrayList<Integer> list = new ArrayList<Integer>();
        
          for(int j = 0 ; j < i ; j++){
                if(j == 0 || j == i - 1 ){
                    list.add(1);
                }else{
                   list.add( lists.get(i-2).get(j)+lists.get(i-2).get(j-1));                                  
                }
            }       

        lists.add(list);     
    }

return lists;
}

 

public boolean isToeplitzMatrix(int[][] matrix){
    int row= matrix.length;
    int col= matrix[0].length;
   //Column direction
    for(int i = 0 ; i < col -1; i++){
        int x = 1;
        int y = i+1;  
        while( x >= 0 && x < row && y >= 0 && y < col){ //Jump out if the condition in the loop is not satisfied
            if(matrix[x][y] != matrix[0][i]){
                return false;

            }
            x++;
            y++;


        }

    }
    //2. directions
        for( int i =  1  ; i < row - 1 ; i ++){
             int x = i + 1;
             int y = 1;
             while(x >= 0 && x < row && y >= 0 && y < col){
                if(matrix[x][y] != matrix[i][0]){
                        return false;
                }
                    x++;
                    y++;
             }

         }



        return true;


}

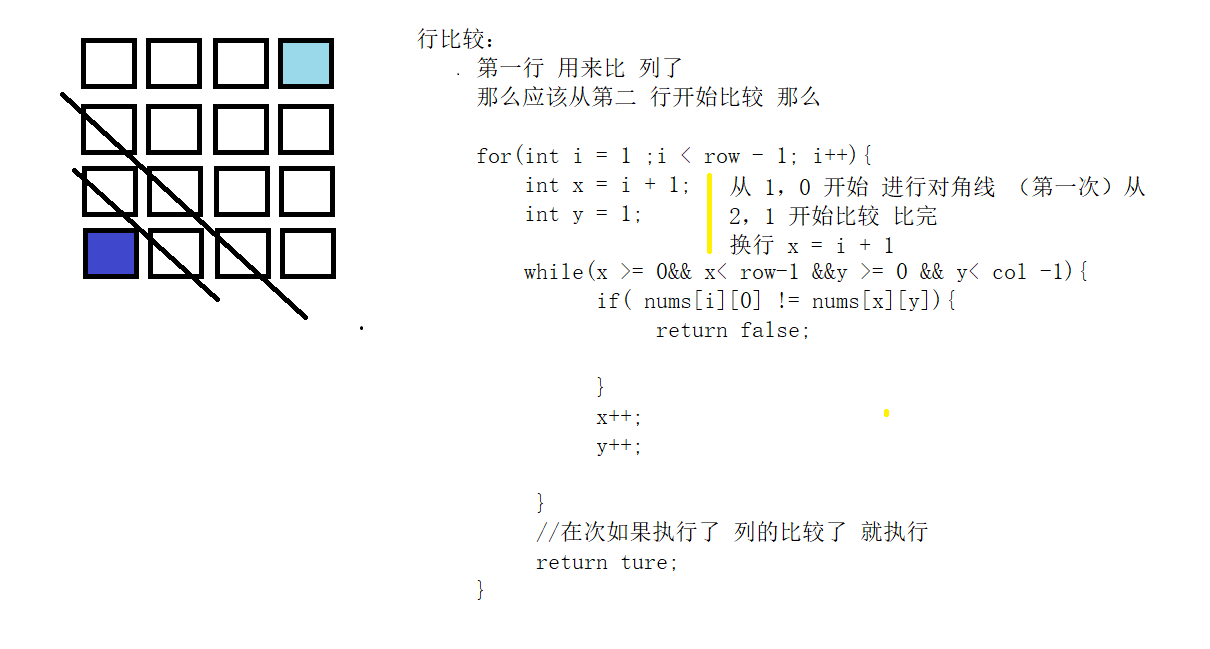
Thoughts: 1. Think about binary array, how to compare.

First: Think about rows and columns. Analyse rectangles. Compare them diagonally.

            

public  boolean canThreeOartsEqualSum( int[] A){

    int sum  = 0;
    for(int a : A){
    
        sum+=a;

    }
    int Tsum = sum / 3;
    int count = 0;
    
    for(int i = 0 ; i < A.length ; i ++){
    
        Tsum -= A[i];
        if( Tsum == 0){
            count++;
            Tsum = sum / 3;

        }

        reutnrn count == 3;
    }












}

 

public int[] toSum(int[] numbers , int target){

    for(int i = 0 ; i < numbers.length ; i ++){
        int index = binarySearch(numbers,i+1,numbers.length-1,target3 - numbers[i]);
            if( index != -1){
             return new int[]={i + 1 , index+1};
            }

    }

           return null;

}

public int binarySearch(int[] arr , int begin , int end ,int key){
    int row = begin;
    int low = end;
    int mid = (row + low)/2;
    while(arr[mid] != key){

        if(arr[mid] > key){

           low = mid - 1;

         }else if(arr[mid] < key){

            row = mid + 1;

        }else if(row > low){
           return -1;
        }
        mid = (row + low)/2;

    }
  return mid;

}

 

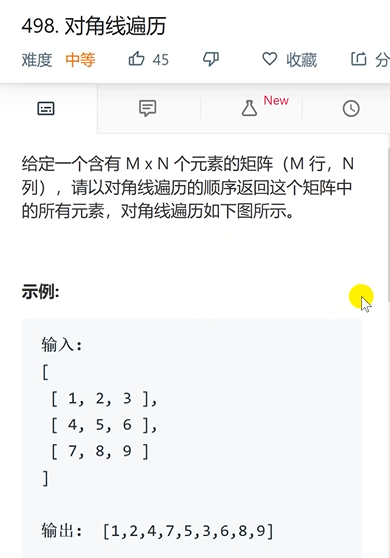
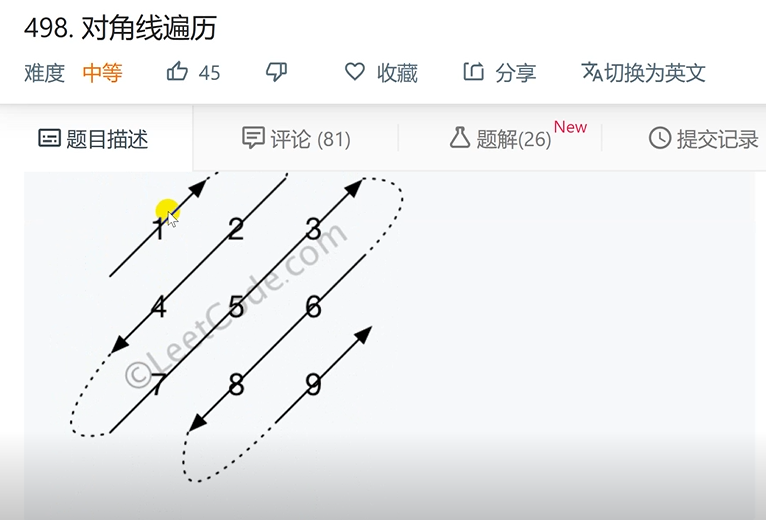
public int[] findDiagonalOrader(int[][] matrix){
    
    //Find row and column lengths for binary arrays
    int row = matrix.length;
    int col = matrix[0].length;
    
    //Define arrays that need to be output
    int[] nums = new int[row * col];
    //Define the point at which the traversal begins (the first point)
    int i = 0;
    int j = 0; 

    //Conditional constraints are null
    if( matrix == null || matrix.length == 0){
        return new int[] {};
     }     
    // Listed as empty   
    if(  col == 0){
    return new int[] {};
     }
    // For a row
    if( col == 1){
        for(int i = 0; i < row ; i ++){
            nums[i] = matrix[i][0];
        }
        return nums;
    }

    int index = 0;   //Subscripts stored as arrays.
    
    while( i < row && j < col){   //Number of cyclically read binary arrays
        
        //Read it and store it in array nums
        nums[index++] = matrix[i][j];
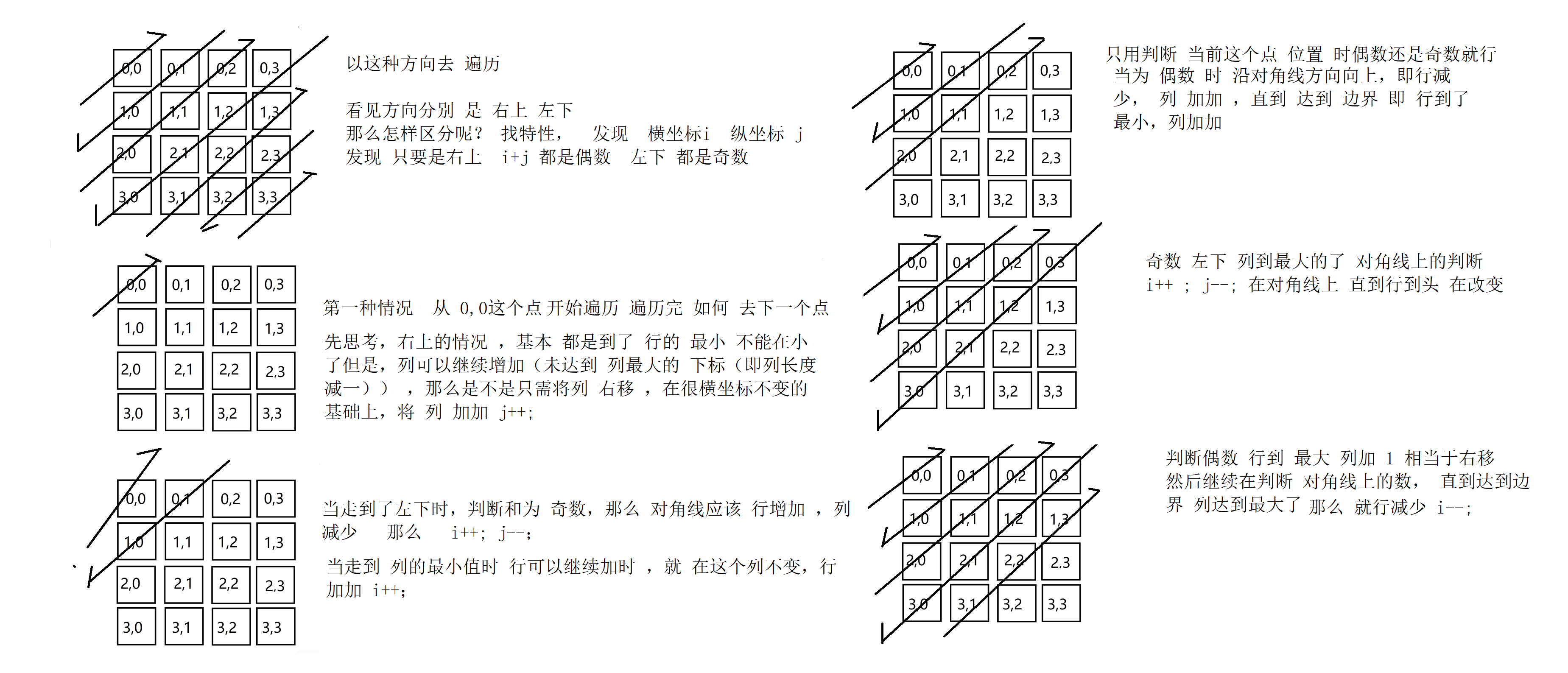
         //According to i + j = even number or odd number, the upper right or lower left segment is judged.
        if( (i + j) % 2 == 0){  // Even upper right
        
            if(i == 0 && j != col -1){  // For example, 0, 0 is a point that can only be traversed to 0, 1.
                j++;
            }else if( j == col -1){
                i++;

            } else{
                i--;
                j++;
        
            }


        }else{
            if( j == 0 && i != row -1){
                i++;
        
             }else if(i == col -1){
                j++;
             }else{
                i++;
                j--;
             }

        }

    }

    return nums;
}