A single normal population
Two normal populations
three Interval estimation of (0-1) parameters
one A normal population
The values here are the upper alpah quantile
| Parameters to be estimated | Other parameters | Distribution of pivot amount | Bilateral confidence interval | Unilateral upper limit | Unilateral lower limit | |
| u | 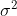 Known Known | 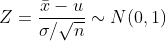 | 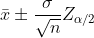 | 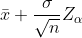 | 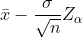 | |
| u | 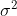 unknown unknown | 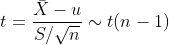 | 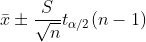 | 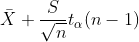 | 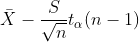 | |
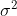 | u unknown | 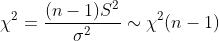 | 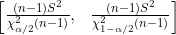 | 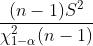 | 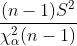 |
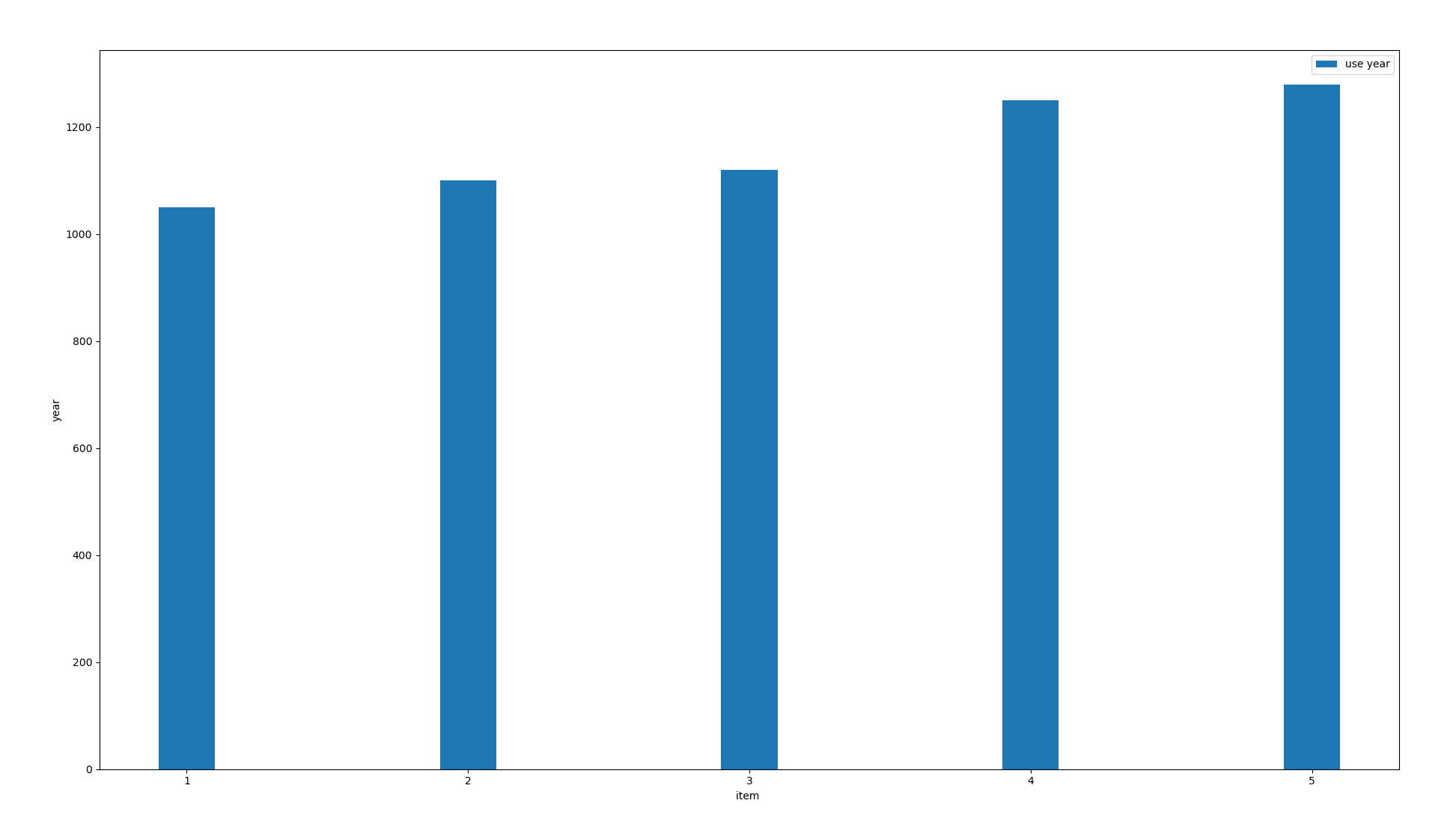
Example: Five bulbs are randomly selected from a batch of bulbs for life test, and the life is measured
1050 1100 1120 1250 1280
Let the bulb obey the normal distribution, and find the lower limit of one-sided confidence interval with the average confidence level of 0.95
# -*- coding: utf-8 -*-
"""
Created on Sat Nov 20 20:54:34 2021
@author: cxf
"""
import numpy as np
from scipy.stats import t
import matplotlib.pyplot as plt
class Confidence():
def GetData(self):
data =[1050, 1100,1120,1250,1280]
x = np.arange(1,len(data)+1)
plt.bar(x, data,width=0.2, label='use year')
plt.xlabel("item ")
plt.ylabel("year")
plt.legend()
plt.show()
return data
def __init__(self):
self.alpha = 0.05 #The confidence interval was 0.95
'''
ddof= 1 Is the sample standard deviation, otherwise it is the overall standard deviation
'''
def GetConfidence(self):
data = self.GetData()
n = len(data)
x_bar = np.mean(data)
s = np.std(data,ddof=1)
v = t.isf(self.alpha,n-1)
print("\n Sample mean %5.2f ,Sample standard deviation %5.2f Number of samples %d , upper alpha Quantile%5.2f "%(x_bar, s,n,v))
low = x_bar-s/np.sqrt(n)*v
print("\n Lower limit of unilateral confidence interval u %5.2f"%low)
if __name__ == "__main__":
Co = Confidence()
Co.GetConfidence()
=======================================
Sample mean 1160.00 ,Sample standard deviation 99.75 Number of samples 5 , upper alpha Quantile 2.13
Lower limit of unilateral confidence interval u 1064.90Two normal populations
| Parameters to be estimated | Other parameters | Distribution of pivot amount | Bilateral confidence interval | Unilateral upper limit | Unilateral lower limit |
| u1-u2 | 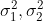 Known Known | 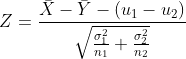 | 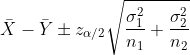 | 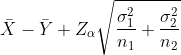 | 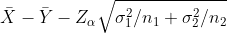 |
| u1-u2 | 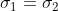 unknown unknown | 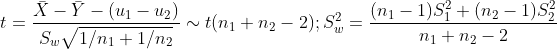 | 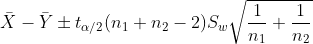 | 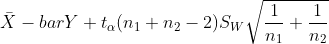 | 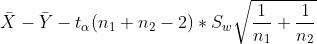 |
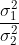 | 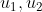 unknown unknown | 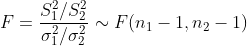 | 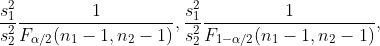 | 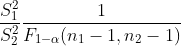 | 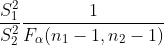 |
three Interval estimation of (0-1) distribution parameters
Sample mean u, variance p(1-p)
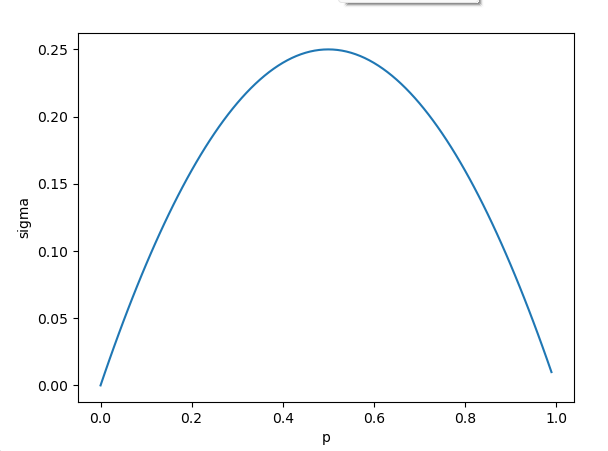
Distribution of pivot amount:
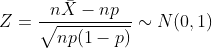
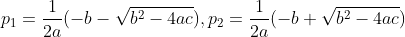
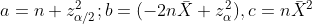
confidence interval
Binomial distribution is
In probability theory and statistics, binomial distribution is a discrete probability distribution of the number of successes in n independent success / failure tests, in which the success probability of each test is p. Such a single success / failure test is also called Bernoulli test . In fact, when n=1, the binomial distribution is Bernoulli distribution.
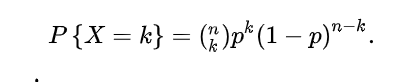
For example, in the KNN algorithm, the general algorithm does not stipulate that we finally take several K numbers from N numbers.
Because the number of K is closest to the Euclidean distance of the sample, D(Xk)=0 is expected to be a type.
For example, if the label type of the sample is 5, the probability of selecting a random sample in k and the label value p of the data itself is
1/N.
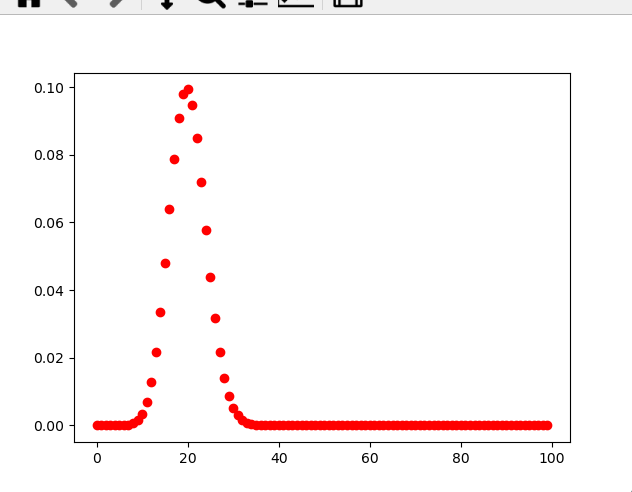
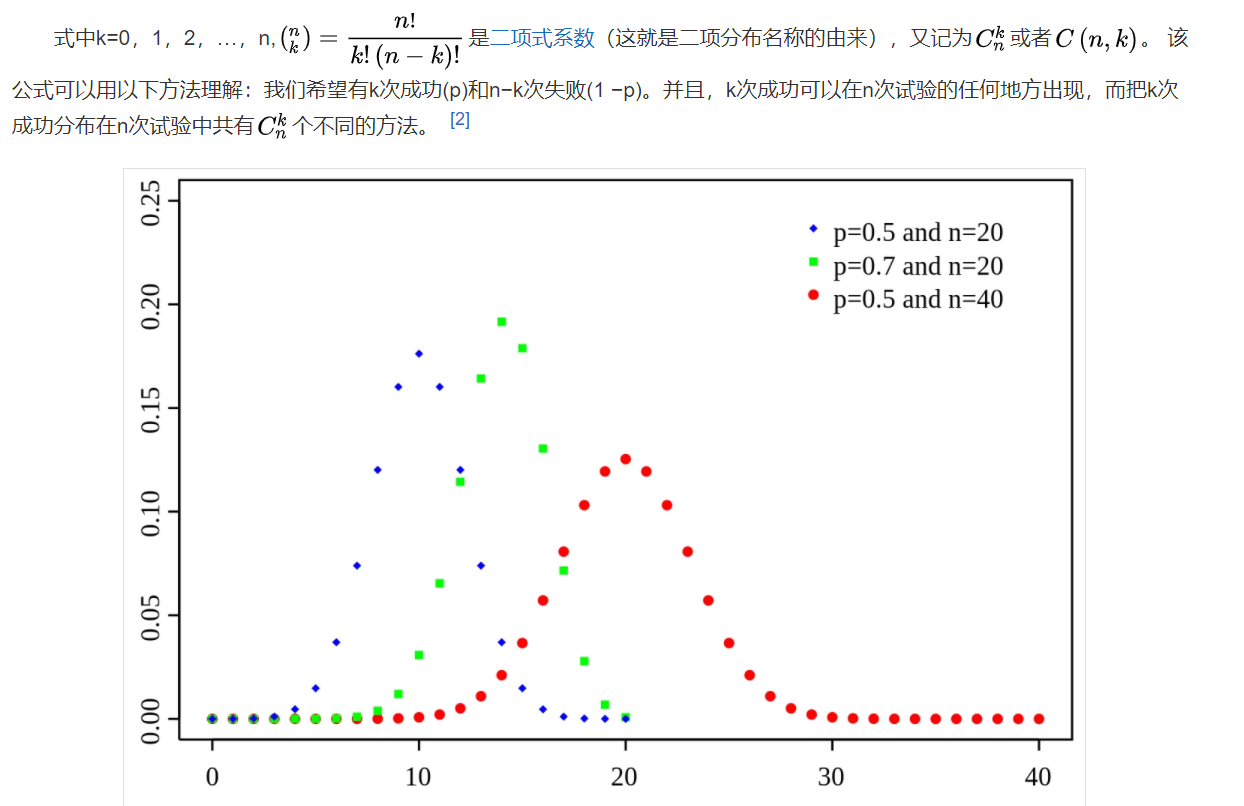
As can be seen from Fig. 1, for fixed n and P, when k increases, the probability P{X=k} first increases until it reaches the maximum, and then decreases monotonically. It can be proved that the general binomial distribution also has this property, and: [1]
-
When (n+1) P is not an integer, the binomial probability P{X=k} reaches the maximum when k=[(n+1)p]; [1]
-
When (n+1) P is an integer, the binomial probability P{X=k} reaches the maximum when k=(n+1)p and k=(n+1)p-1.
example
# -*- coding: utf-8 -*-
"""
Created on Sun Nov 21 16:08:06 2021
@author: cxf
"""
import matplotlib.pyplot as plt
import numpy as np
import scipy.misc as ms
from scipy.special import comb ,perm
def GetP(p,m,n,cb):
a = cb*np.power(p,n)*np.power(1-p,m-n)
return a
def GetData(m,p):
y =[]
x = np.arange(0,m)
for n in range(m):
a = comb(m,n) #Permutation and combination
b = np.power(p,n)
c = np.power(1.0-p,m-n)
#print("cb ",False)
d = a*b*c
y.append(d)
print("prob ",p)
plt.scatter(x,y,c='r')
plt.show()
def DrawTwo():
a= 0
GetData(100,0.2)
DrawTwo()