Looking for "single dog" programming problem summary

The single dog problem is to find the number that only appears once in the array. Others are one-to-one pairs (the number has appeared twice in the array), and only it is a person (there is only one in the array). It is particularly eye-catching like the "single dog". However, the problem can continue to extend, and there can be two or even three single dogs. The following is a personal summary of all kinds of single dog problems. Compared with similar articles, this summary will be more comprehensive.

1, There is only one single dog

Method 1:
Sort first and then compare (see on the Internet). First, use bubble sorting to sort the array elements (from large to small or from small to large). After sorting, the same elements will be adjacent to each other, so we only need to compare the adjacent elements in pairs to find the one handed dog (think about the picture: originally, everyone stood scattered and matched one by one (violence solving method) Now, if you let your boyfriend and girlfriend hold hands next to each other, the one handed dog can only stand there alone. You can see it at a glance in the past).
Unfortunately, the imagination is beautiful, but this method has a big problem. When the singular number has the tail of the array, this loop detection method will have cross-border access, and the time complexity of this method is not good, so this method cannot be used.

//Only one single dog
// Method 1
void Bubble_sort(int* p,size_t sz)
{
	size_t i = 0;
	for (i = 0; i < sz; i++)
	{
		size_t j = 0;
		for (j = 0; j < sz-i-1; j++)
		{
			while (*(p + j) > *(p + j + 1))
			{
				int tmp = *(p + j);
				*(p + j) = *(p + j + 1);
				*(p + j + 1) = tmp;
			}
		}
	}
}
int main()
{
	int arr[] = { 1,2,3,4,5,4,3,2,1 };
	size_t sz = sizeof(arr) / sizeof(arr[0]);
	//Sort first
	Bubble_sort(arr,sz);
	size_t i = 0;
	for (i=0;i<sz;)
	{ 
		//After sorting, the same numbers will be together, so close comparison. If they are the same, skip this pair
		if (arr[i] == arr[i + 1])
		{
			i = i + 2;
	}
		//If not, the element at i position is output
		else
		{
			printf("%d", arr[i]);
			i++;
		}

	}
	
		return 0;
}

Method 2:

Use the XOR operator. One characteristic of XOR operator is that two binary representations are 1 if they are different and 0 if they are the same.
If you don't understand, you can see this https://www.dotcpp.com/course/606 .
We just need to XOR 0 and each element in the array in turn, and the final result is the number we are looking for (single dog).

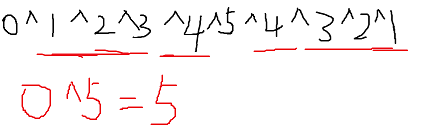
//Method 2
int main()
{
		int arr[] = { 1,2,3,4,5,4,3,2,1 };
		int i = 0;
		int ret = 0;
		int sz = sizeof(arr) / sizeof(arr[0]);
		for (i = 0; i < sz; i++)
		{
			ret = ret ^ arr[i];
		}
		printf("%d\n", ret);

2, Two single dog problems

I specifically searched how to solve the problem of "two single dogs", and found that part of the answer is based on knowing which two single dogs are in advance, and then separating them according to the binary characteristics of the two single dogs. Obviously, this is unreasonable. We should find out the single dog without knowing what the two single dogs are.

#include<stdio.h>
#include<stdlib.h>


int main()
{
	int a[] = { 1,2,3,4,5,1,2,3,4,6 };
	int n[5] = { 0 };
	int m[5] = { 0 };
	int i = 0,j = 0,k = 0;
	int ret = 0,ret1 = 0,ret2 = 0;
	int count = 0,count1 = 0;
	int s = sizeof(a) / sizeof(a[0]);
	//All numbers are XORed with 0 to get ret, and the result should be the XOR of two single dogs (5 ^ 6)
	for (i = 0; i < s; i++)
	{
		ret ^= a[i];
	}

	//Starting from the first bit to the last bit, the binary numbers of the two single dogs must have one or several different positions. We just need to traverse to find the differences and transfer them to different arrays, which becomes the problem of "a single dog".
		for (i = 0; i < 32; i++)
		{
			for (j = 0; j < s; j++)
			{
				int b =a[j] >> i;
				if ((b & 1)!=0)
				{
					n[count] = a[j];
					++count;
				}
				else
				{
					m[count1] = a[j];
					++count1;
				}
			}
			//Check whether two single dogs are in different arrays
			for (k = 0; k < 5; k++)
			{
				ret1 ^= n[k];
			}
			if (ret1 != ret)
			{
				break;
			}

		}
		for (k = 0; k < 5; k++)
		{
			ret2 ^= m[k];
		}
		printf("[%d,%d]", ret1, ret2);
}

3, There are three single dog problems

Similarly, it can be divided into two single dogs and one single dog; Two single dogs can be split into one single dog problem. By analogy, there will be no more complaints here.

In addition, it suddenly occurred to me that the problem of single dogs can also be turned into the problem of finding even numbers. If it is difficult to find single dogs, then find even numbers. The rest is single dogs. This method should also be feasible.