In this blog, we will introduce a super efficient algorithm for super cancer
Line tree

Concept introduction

First of all, let's get to know the line tree
What is line tree
Line tree is a kind of binary tree, that is, for a line, we will use a binary tree to express. For example, a line with a length of 6 can be expressed as follows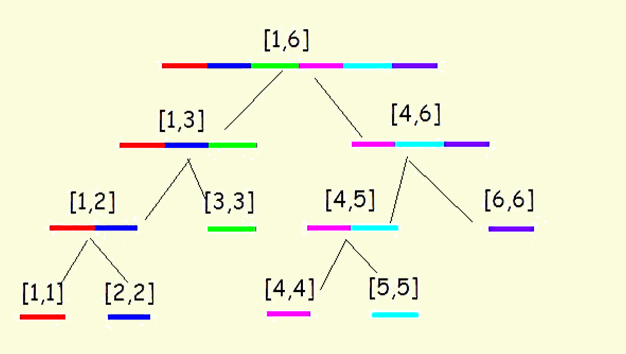

What does this picture mean?

• Make this into a tree structure. Each root node stores the sum of the weights of the left and right nodes
  Take a chestnut: the top line represents the sum of 1-6, while his left son represents 1-3 and his right son represents 4-6
  
• Then the left son of his left son represents the weight of 1-2 and the right son of his left son represents the weight of 3
• So the weight of node i = I the weight of left son + I the weight of right son
• So we can get tree[rt].sum = tree[l].sum + tree[r].sum
• According to this principle, we can build trees recursively

struct node{
      int l,r,sum;//l represents the left son r represents the right son sum represents the weight stored in the current node
}tree[maxn*4];

void build(int i,int l,int r){
	tree[i].l = l;tree[i].r = r;
	if(l == r){
		tree[i].sum = a[l];//a array stores the given array initial value
		return;
	}
	int mid = (l+r)/2;
	build(i*2,l,mid);
	build(i*2+1,mid+1,r);
	tree[i].sum = tree[i*2].sum+tree[i*2+1].sum;
	return;
}

This is the tree building method of line segment tree. If you want to ask why we need to spend several times of memory to build trees to complete an array, that's because we need to let this super large array do some difficult things
So what's more difficult? Let's move on to the next topic

Simple operation

Single point modify interval query

• For example, we require the sum of intervals 1 to 5
• Obviously, for (int i = 1; I < = 5; + + I) {ans + = a [i]};
• But we still need to use the line tree to operate
• First look at the location of the interval
  Currently, the left boundary of root node storage is 1, and the right boundary is 6
  The left boundary of the left son of the root node is 1. The right boundary is 3. The left boundary of the right son is 4. The right boundary is 6
  The interval of the left son is completely included in the interval, so we directly return the weight of the left son
  The left boundary of the right son is on the left of the right boundary of the target interval, so we continue to search the right boundary recursively
  Now the latest left son is 4-5, which is completely included in the target interval, and directly returns the weight. Right son 6 has nothing to do with this interval and returns 0
  Now we can add up the returned value by 3 + 2 = 5
  
  
  
  
  
  
• Some people may be able to make complaints about what is going to be solved by using an array.
• But sometimes the array is very convenient, but it can't meet our needs. Sometimes the efficiency of O(n) can't make the author happy. At this time, the line tree o (\ (log) is needed_ n\))

So how to implement it with code is very simple
Let's summarize the query method of line tree:

• If the current interval is completely included in the target interval, directly return the weight of the current interval
• If the current interval has nothing to do with the target interval, return to 0 directly
• If the current interval crosses the target interval, continue to search the left and right sons recursively
  Then we can have such a code implementation form
  

int search(int rt,int l,int r){
	if(tree[rt].r < l ||tree[rt].l > r)return 0;
	if(tree[rt].l >= l && tree[rt].r <= r)return tree[rt].sum;
	int ans = 0;
	if(tree[rt*2].r >= l)ans += search(2*rt,l,r);
	if(tree[rt*2+1].l <= r)ans += search(2*rt+1,l,r);
	return ans;
}

What about the single point of modification
This is much simpler

• Give a position x a value k
• If we want to change the number of x positions to add a number k, we will let the tree recursively find this position

void add(int rt,int x,int k){
	if(tree[rt].l == tree[rt].r){//Reach the leaf node description to find the location
		tree[rt].sum += k;
		return;
	}
	if(x <= tree[rt*2].r)add(rt*2,x,k); // Recursive search left son
	else add(rt*2+1,x,k);//Recursive search right son
	tree[rt].sum = tree[rt*2].sum + tree[rt*2+1].sum;//Add weight again
	return;
}

Single point query of interval modification

There are many methods for interval modification and single point query
In order to explain the pushdown later, let's talk about a method that is more convenient for the following understanding

Interval modification is very similar to interval query

• However, in the interval query, if the current interval is completely included in the target interval, the value of the current interval will be returned. Instead, the current interval will be marked with k
• For example, let's add all the numbers of an interval to k
• If the interval of a segment tree is completely included in the target interval, mark the interval with k
• But we're going to make a difference here
• Because the initial value of all our nodes will be 0 (for the convenience of recording the mark k)

void build(int l,int r,int rt){
    tree[rt].num=0;
    tree[rt].l=l;
    tree[rt].r=r;
    if(l==r)
        return ;
    int mid=(r+l)/2;
    build(l,mid,rt*2);
    build(mid+1,r,rt*2+1);
}

void add(int rt,int l,int r,int k){
    if(tree[rt].l>=l && tree[rt].r<=r){
        tree[rt].num+=k;
        return ;
    }
    if(tree[rt*2].r>=l)
       add(rt*2,l,r,k);
    if(tree[rt*2+1].l<=r)
       add(rt*2+1,l,r,k);
}

A single point query can find all the tags encountered on the way to this node, and then add the initial value of this node
It's like this in code

void search(int rt,int dis){
    ans+=tree[rt].num;
    if(tree[rt].l==tree[rt].r)
        return ;
    if(dis<=tree[rt*2].r)
        search(rt*2,dis);
    if(dis>=tree[rt*2+1].l)
        search(rt*2+1,dis);
}
    //In the main function
    printf("%d\n",ans+a[x]);//a[x] is the initial value of the target position

It is recommended to finish the above board and continue to watch it downward

Interval modification and query (pushdown and lazy)

Difficulties ahead
If you see such a question, do you think it's just the two above that are put together
But if you do, you'll find WA
Why?


Let's think back to what we just did: when we mark the interval, we will find it from the top down, accumulate the marks, and then add the initial value


But is that really OK?


The answer is No. the reason is very simple: if you ask for the sum of 1-3 intervals and you just mark the 3-5 intervals, because 1-3 does not contain the marks of 3-5, so our calculated result is not the sum of k but the sum of initial values


How to solve this problem? It's also very simple: just put our mark k on the son of i


So the rudiments of our algorithm come out (this is also the most poisonous and charming part of line tree)

• First of all, we define another variable, lazy, in the structure to record the tag's addition every time we add it to lazy
• The next step is to pull down the operation to drop lazy into the son node of i
• So through simple reasoning and induction, we still have the following properties:
    1. If the current interval is completely included in the target interval, then the weight of this interval tree[rt].sum += k*(tree[rt].r - tree[rt].l + 1)
    2. If there is an intersection between the current interval and the target interval, but it is not completely covered, drop the lazy flag
    3. Perform the same operation on the left son and the right son respectively after lowering
  
  
  
• Finally, it is still updated according to tree[rt].sum = tree[rt2].sum + tree[rt2+1].sum
  So the code implementation is
  

void pushdown(long long rt){
	if(tree[rt].lazy != 0){//If the current range has been marked
		tree[rt*2].lazy += tree[rt].lazy;//Down to left son
		tree[rt*2+1].lazy += tree[rt].lazy;//Down to right son
		long long mid = (tree[rt].l + tree[rt].r)/2;
		tree[rt*2].sum += tree[rt].lazy*(mid - tree[rt*2].l + 1);//Update left son's value
		tree[rt*2+1].sum += tree[rt].lazy*(tree[rt*2+1].r - mid);//Update right son's value
		tree[rt].lazy = 0;//Clear the lazy flag of the current node
	}
	return;
}

void add(long long rt,long long l,long long r,long long k){
	if(tree[rt].l >= l && tree[rt].r <= r){//If the current range is completely included in the target range, update it directly and mark the lazy flag
		tree[rt].sum += k*(tree[rt].r-tree[rt].l+1);//Update the weight of the current interval
		tree[rt].lazy += k;//Add lazy tag
		return;
	}
	pushdown(rt);//Put down the lazy mark
	if(tree[rt*2].r >= l)add(rt*2,l,r,k);//Recursively update left son
	if(tree[rt*2+1].l <= r)add(rt*2+1,l,r,k);//Recursive update right son
	tree[rt].sum = tree[rt*2].sum+tree[rt*2+1].sum;//Update the weight of the current node
	return;
}

The interval query is almost the same as the previous one, which is to drop the lazy flag and accumulate it

long long search(long long rt,long long l,long long r){
	if(tree[rt].l >= l && tree[rt].r <= r)return tree[rt].sum;//If the current interval is completely included in the target interval, directly return the weight of the current interval
	if(tree[rt].r < l || tree[rt].l > r)return 0;//If there is no relationship between the current interval and the target interval, return to 0 directly
	pushdown(rt);//Put down the lazy mark
	long long s = 0;
	if(tree[rt*2].r >= l)s += search(rt*2,l,r);
	if(tree[rt*2+1].l <= r)s += search(rt*2+1,l,r);
	return s;//Finally return the sum of this interval
}

The line tree model is just like this (is it because it is difficult to adjust?? )
Attach the exercise strategy:
Recommended for simple line tree Luogu P3374 [template] tree array 1
        Luogu P3368 [template] tree array 2 Exercise board
If the simple line tree is OK
Try it: Luogu P3372 [template] line tree 1
        Luogu P3373 [template] line tree 2
        Luogu P6242 [template] line tree 3

Thanks for watching
Focus >_<