A small scalpel
Topic: Given an array, judgment is that the sum of subsets is 100
- Recursive Solution
# param: arr is an array, i is an array length - 1, and target is the target number (100) def recur_subset(arr, i, target): if arr[i] == target: return True if i == 0: return arr[0] == target if arr[i] > target: return dp_recur(arr, i-1, target) else: A = dp_recur(arr, i-1, target-arr[i]) B = dp_recur(arr, i-1, target) return A or B
- dynamic programming
import numpy as np # params: arr is a given array, target is the target number (100) def dp_subset(arr, target): length = len(arr) # Element index with arr vertically and target horizontally dp = np.zeros((len(arr), target+1)) # When the arr[0] is reached, it will be set to False instead of arr[0] and True equally. dp[0, :] = False # When target is 0, return True, that is, two-dimensional dp is listed as True first. dp[:, 0] = True # Judge the boundaries, if arr [0] > target, then cross the boundaries if arr[0] < target: dp[0, arr[0]] = True for i in range(1, len(arr)): for j in range(1, target+1): if arr[i] > j: dp[i, j] = dp[i-1, j] else: A = dp[i-1, j-arr[i]] B = dp[i-1, j] dp[i, j] = A or B print(dp) return dp[-1, -1]
leetcode 5. longest palindrome substring
Given a string s, find the longest palindrome substring in S. You can assume that the maximum length of S is 1000.
Example 1:
Input: "babad"
Output: "bab"
Note that "aba" is also an effective answer.
Example 2:
Input: "cbbd"
Output: "bb"
Source: LeetCode
Links: https://leetcode-cn.com/problems/longest-palindromic-substring
Copyright belongs to the seizure network. For commercial reprints, please contact the official authorization. For non-commercial reprints, please indicate the source.
Problem Solutions (Dynamic Programming):
class Solution(object):
def longestPalindrome(self, s):
"""
:type s: str
:rtype: str
"""
if len(s) <= 1:
return s
length = len(s)
# Create a two-dimensional dp list
dp = [[False for _ in range(length)] for _ in range(length)]
max_length = 1
res = s[0]
for r in range(1, length):
for l in range(r):
# If the first s[l] and the last s[r] are equal, and the middle substring is also a palindrome string or the length of the substring is less than or equal to 1, then this is a palindrome string.
if s[l] == s[r] and (r-l <= 2 or d[l+1][r-1]):
dp[l][r] = True
cur_length = r - l + 1
if cur_length > max_length:
max_length = cur_length
res = s[l:r+1]
return res
leetcode 53. Maximum subsequence sum
Given an integer array nums, find a continuous subarray with the largest sum (the subarray contains at least one element) and return its maximum sum.
Examples:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Interpretation: The sum of continuous subarrays [4, -1, 2, 1] is the largest, which is 6.
Source: LeetCode
Links: https://leetcode-cn.com/problems/maximum-subarray
Copyright belongs to the seizure network. For commercial reprints, please contact the official authorization. For non-commercial reprints, please indicate the source.
class Solution(object):
def maxSubArray(self, nums):
"""
:type nums: List[int]
:rtype: int
"""
res = nums[0]
max_sum = 0
for i in nums:
if max_sum > 0:
max_sum += i
else:
max_sum = i
res = max(res, max_sum)
return res
leetcode 62. Different Paths I
A robot is located in the upper left corner of an m x n grid (the starting point is marked "Start" in the figure below).
The robot can only move down or right one step at a time. The robot tries to reach the lower right corner of the grid (marked "Finish" in the figure below).
How many different paths are there altogether?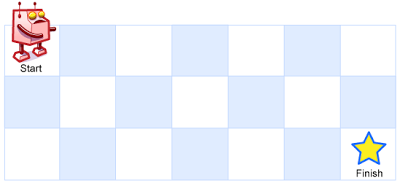
For example, the figure above is a 7 x 3 grid. How many possible paths are there?
Note: The values of m and n are not more than 100.
Example 1:
Input: m = 3, n = 2
Output: 3
Explanation:
Starting from the upper left corner, there are three paths to the lower right corner.
- Right - > Right - > Down
- Right - > Down - > Right
- Down - > Right - > Right
Example 2:
Input: m = 7, n = 3
Output: 28
Source: LeetCode
Links: https://leetcode-cn.com/problems/unique-paths
Copyright belongs to the seizure network. For commercial reprints, please contact the official authorization. For non-commercial reprints, please indicate the source.
class Solution(object):
def uniquePaths(self, m, n):
"""
:type m: int
:type n: int
:rtype: int
"""
if m == 1 or n == 1:
return 1
dp = [[0 for _ in range(m)] for _ in range(n)]
for i in range(n):
for j in range(m):
if i == 0:
dp[i][j] = 1
if j == 0:
dp[i][j] = 1
else:
dp[i][j] = dp[i-1][j] + dp[i][j-1]
# print(dp)
return dp[-1][-1]
leetcode 63. different paths II
A robot is located in the upper left corner of an m x n grid (the starting point is marked "Start" in the figure below).
The robot can only move down or right one step at a time. The robot tries to reach the lower right corner of the grid (marked "Finish" in the figure below).
Now consider the obstacles in the grid. So how many different paths will there be from the top left to the bottom right?
Obstacles and empty positions in the grid are represented by 1 and 0, respectively.
Note: The values of m and n are not more than 100.
Example 1:
Input:
[
[0,0,0],
[0,1,0],
[0,0,0]
]
Output: 2
Explanation:
There is an obstacle in the middle of the 3x3 grid.
There are two different paths from the upper left corner to the lower right corner:
- Right - > Right - > Down - > Down
- Down - > Down - > Right - > Right
Source: LeetCode
Links: https://leetcode-cn.com/problems/unique-paths-ii
Copyright belongs to the seizure network. For commercial reprints, please contact the official authorization. For non-commercial reprints, please indicate the source.
class Solution(object):
def uniquePathsWithObstacles(self, obstacleGrid):
"""
:type obstacleGrid: List[List[int]]
:rtype: int
"""
row = len(obstacleGrid)
col = len(obstacleGrid[0])
dp = [[0 for _ in range(col)] for _ in range(row)]
for i in range(row):
for j in range(col):
if obstacleGrid[i][j] == 1:
dp[i][j] = 0
continue
if i == 0 and j == 0:
if obstacleGrid[i][j] == 1:
return 0
else:
dp[i][j] = 1
elif i == 0 and j >= 1:
print('xbb')
dp[i][j] = dp[i][j-1]
elif j == 0 and i >= 1:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = dp[i][j-1] + dp[i-1][j]
return dp[-1][-1]
leetcode 120. minimum path sum of triangles
Given a triangle, find the minimum path sum from top to bottom. Each step can only move to adjacent nodes in the next row.
For example, given a triangle:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The sum of the top-down minimal paths is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Source: LeetCode
Links: https://leetcode-cn.com/problems/triangle
Copyright belongs to the seizure network. For commercial reprints, please contact the official authorization. For non-commercial reprints, please indicate the source.
class Solution(object):
def minimumTotal(self, triangle):
"""
:type triangle: List[List[int]]
:rtype: int
"""
if len(triangle) == 0:
return 0
# Walk through each line in turn from the penultimate line
row = len(triangle) - 2
for i in range(row, -1, -1):
for j in range(len(triangle[i])):
# Take the next row and add the smaller of the two adjacent numbers.
triangle[i][j] += min(triangle[i+1][j], triangle[i+1][j+1])
return triangle[0][0]
leetcode 121. the best time to buy and sell stocks
Given an array, its first element is the price of a given stock on the first day.
If you allow at most one transaction to be completed (that is, buying and selling a stock), design an algorithm to calculate the maximum profit you can make.
Note that you can't sell stocks before buying them.
Example 1:
Input: [7, 1, 5, 3, 6, 4]
Output: 5
Explanation: Buy on the second day (stock price = 1) and sell on the fifth day (stock price = 6). Maximum profit = 6-1 = 5.
Note that the profit should not be 7-1 = 6, because the selling price needs to be greater than the buying price.
Example 2:
Input: [7, 6, 4, 3, 1]
Output: 0
Explanation: In this case, no transaction is completed, so the maximum profit is 0.
Source: LeetCode
Links: https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock
Copyright belongs to the seizure network. For commercial reprints, please contact the official authorization. For non-commercial reprints, please indicate the source.
Idea 1
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
buy = prices[0]
profit = [0 for _ in range(len(prices))]
for i in range(len(prices)):
if prices[i] > buy:
profit[i] = prices[i] - buy
else:
buy = prices[i]
return max(profit)
Idea 2
class Solution_1(object):
def maxProfit(self, prices):
min_price = prices[0]
max_profit = 0
for i in range(len(prices)):
min_price = min(min_price, prices[i])
max_profit = max(max_profit, prices[i] - min_price)
return max_profit
leetcode 122. Best time to buy and sell stocks II
Given an array, its first element is the price of a given stock on the first day.
Design an algorithm to calculate the maximum profit you can make. You can do as much trading as you can (buy and sell a stock many times).
Note: You can't participate in multiple transactions at the same time (you have to sell your previous shares before you buy again).
Example 1:
Input: [7, 1, 5, 3, 6, 4]
Output: 7
Explanation: Buy on the second day (stock price = 1) and sell on the third day (stock price = 5), and the exchange will make a profit = 5-1 = 4.
Then, buy on the fourth day (stock price = 3) and sell on the fifth day (stock price = 6), and the exchange will make a profit = 6-3 = 3.
Example 2:
Input: [1, 2, 3, 4, 5]
Output: 4
Explanation: Buy on the first day (stock price = 1) and sell on the fifth day (stock price = 5), and the exchange will make a profit = 5-1 = 4.
Note that you can't buy stocks on the first and second days and sell them later.
Because it's a combination of transactions, you have to sell your previous shares before you buy again.
Example 3:
Input: [7, 6, 4, 3, 1]
Output: 0
Explanation: In this case, no transaction is completed, so the maximum profit is 0.
Source: LeetCode
Links: https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-ii
Copyright belongs to the seizure network. For commercial reprints, please contact the official authorization. For non-commercial reprints, please indicate the source.
Algorithms 1: Peak and Valley Method
Assume that the given array is:
[7, 1, 5, 3, 6, 4]
If we draw numbers in a given array on a graph, we will get: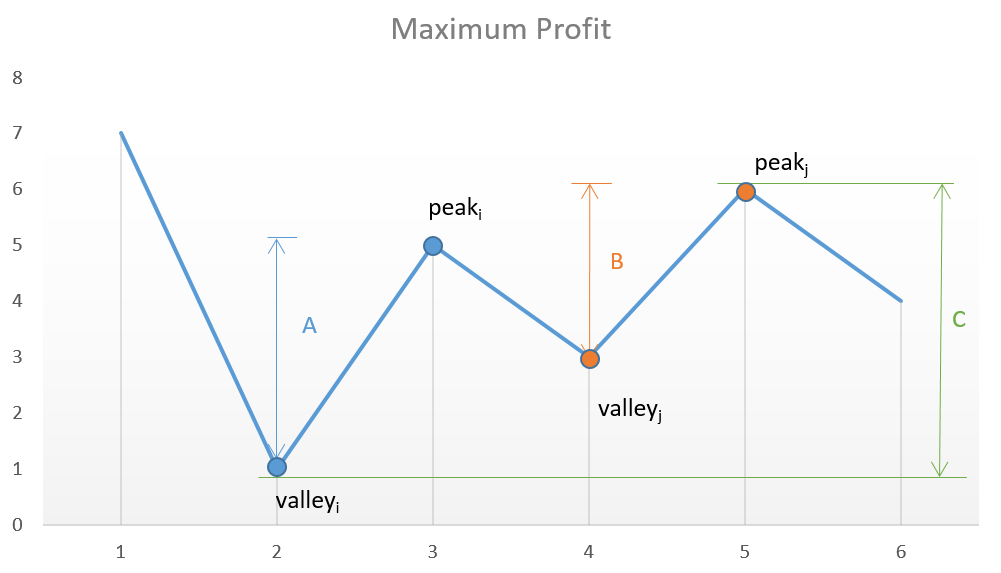
If we analyze charts, our interest points are successive peaks and valleys.
Described in mathematical language as follows: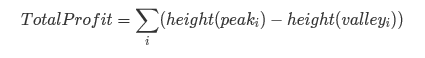
The key is that we need to take into account every peak in the valley to maximize profits. If we try to skip one of the peaks to make more profits, we will eventually lose the profits from one of the transactions, resulting in a decrease in total profits.
For example, in the above case, if we skip peak_i and valley_j and try to gain more profits by considering the points with larger differences, the net profit will always be smaller than the static profit that includes them, because C is always smaller than A+B.
Author: LeetCode
Links: https://leetcode-cn.com/problems/two-sum/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-ii-by-leetcode/
Source: LeetCode
Copyright belongs to the author. For commercial reprints, please contact the author for authorization. For non-commercial reprints, please indicate the source.
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if len(prices) < 2:
return 0
profit = 0
peek = prices[0]
valley = prices[0]
i = 0
while i < len(prices)-1:
while i < len(prices)-1 and prices[i] >= prices[i+1]:
i += 1
valley = prices[i]
while i < len(prices)-1 and prices[i] <= prices[i+1]:
i += 1
peek = prices[i]
profit += peek - valley
return profit
Algorithms 2: Simple traversal
[1, 7, 2, 3, 6, 7, 6, 7]
The graph corresponding to this array is: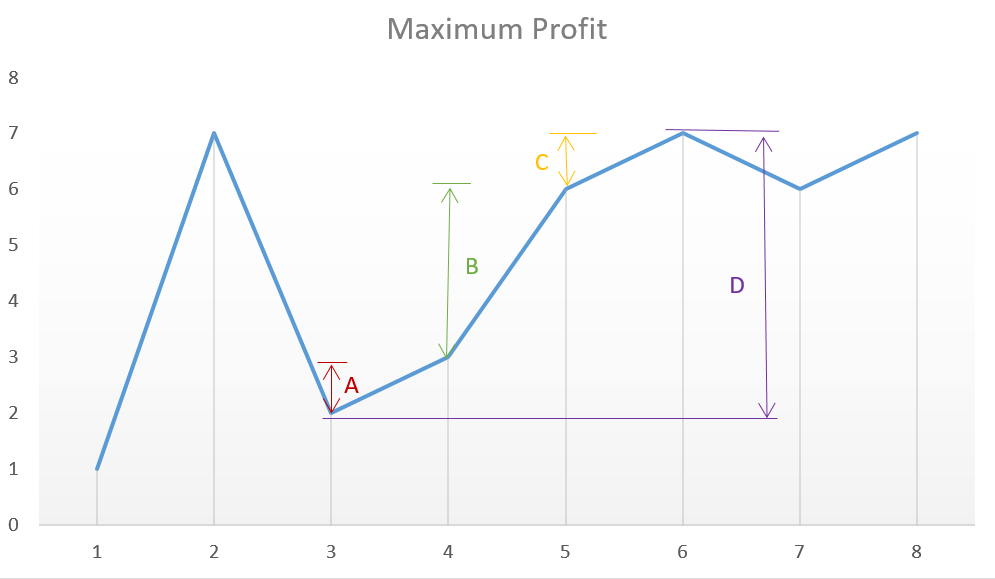
From the above figure, we can observe the difference between the height of continuous peaks and valleys corresponding to the sum of A+B+C and the difference D.
Author: LeetCode
Links: https://leetcode-cn.com/problems/two-sum/solution/mai-mai-gu-piao-de-zui-jia-shi-ji-ii-by-leetcode/
Source: LeetCode
Copyright belongs to the author. For commercial reprints, please contact the author for authorization. For non-commercial reprints, please indicate the source.
class Solution(object):
def maxProfit(self, prices):
"""
:type prices: List[int]
:rtype: int
"""
if len(prices) < 2:
return 0
profit = 0
for i in range(len(prices)-1):
if prices[i+1] > prices[i]:
profit += prices[i+1] - prices[i]
return profit