1. Force buckle 141: ring linked list

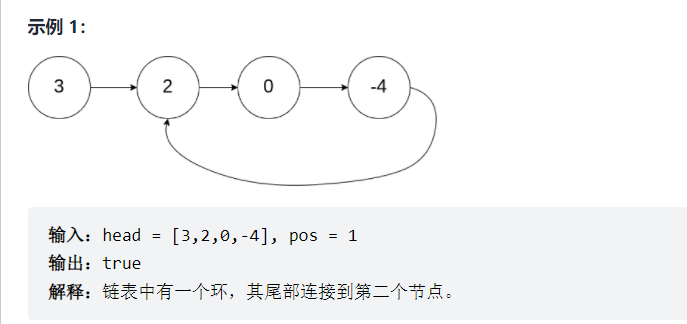
Give you a head node of the linked list to judge whether there are links in the linked list.
If there is a node in the linked list that can be reached again by continuously tracking the next pointer, there is a ring in the linked list. In order to represent the rings in a given linked list, the evaluation system uses the integer pos to represent the position where the tail of the linked list is connected to the linked list (the index starts from 0). If pos is - 1, there is no ring in the linked list. Note: pos is not passed as a parameter, but only to identify the actual situation of the linked list.
Returns true if there are links in the linked list. Otherwise, false is returned.

analysis:
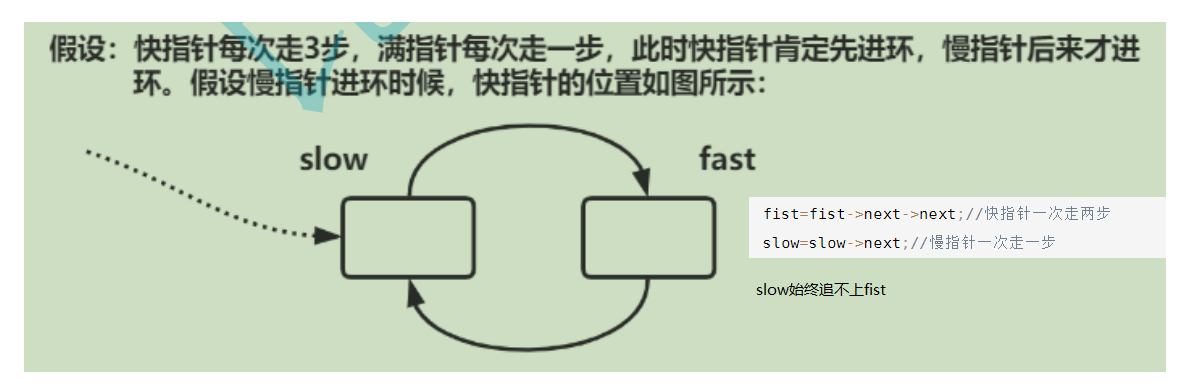
1. Let the fast pointer take two steps at a time and the slow pointer take one step at a time. If they meet, there will be a ring
2. When the fast pointer goes to NULL, it indicates that there is no ring

bool hasCycle(struct ListNode *head) {
    struct ListNode* fist=head;
    struct ListNode* slow=head;
    while(fist&&fist->next){
        fist=fist->next->next;//Go two steps at a time
        slow=slow->next;//Slow the pointer one step at a time
        if(fist==slow){
            return true;//Meeting shows that there is a ring
        }
    }
    //The fast pointer goes to NULL, indicating that the linked list has no ring
    return false;
}

reflection:
1. Why can the fast pointer take two steps at a time and the slow pointer take one step at a time?
A: assuming that the linked list has a ring, both pointers will finally enter the ring. The fast pointer will enter the ring first, and the slow pointer will enter the ring later. In the worst case, the distance between two pointers is just the length of the ring. At this time, each time the two pointers move, the distance between them will be reduced by one step, and it will not happen that each time it happens to be a ferrule. Therefore, before the slow pointer goes one circle, the fast pointer can certainly catch up with the slow pointer, that is, meet.
2. Can the fast pointer take three / four steps at a time and the slow pointer take one step at a time?
A: No.
Example:

2. Force buckle 142: find the entrance of the ring linked list

Given a linked list, return the first node from the linked list into the ring. If the linked list is acyclic, null is returned. If there is a node in the linked list that can be reached again by continuously tracking the next pointer, there is a ring in the linked list. In order to represent the rings in a given linked list, the evaluation system uses the integer pos to represent the position where the tail of the linked list is connected to the linked list (the index starts from 0). If pos is - 1, there is no ring in the linked list. Note: pos is not passed as a parameter, but only to identify the actual situation of the linked list. Modification of linked list is not allowed.

analysis:
1. First judge whether there is a ring (i.e. the first problem-solving method)

First give the conclusion: let a pointer traverse the list from the starting position of the list, and let a pointer run around the ring from the position of the meeting point when judging the ring. The two pointers take one step each time, and will eventually meet at the position of the entry point.

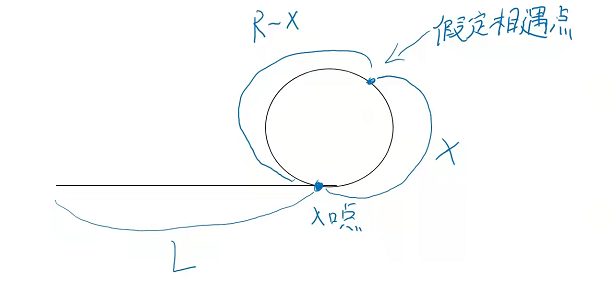
2. When judging whether it is a ring, the fast and slow pointer goes along the path. Fast pointer = L+nR+X, slow pointer = L+X
be careful:
(1) . when the slow pointer enters the ring, the fast pointer has circled the ring n times, n > = 1; Because the fast pointer passes through the meeting point at least once and then meets the slow pointer
(2) After the slow pointer enters the ring, the fast and slow pointers will meet in one circle
The speed of the fast pointer is twice that of the slow pointer: that is, 2 * (L+X) = L+X+nR
That is, L=nR-x (the size of n depends on the size of the ring and the distance from the starting point to the meeting point)
Conclusion: one pointer goes from the starting position of the linked list, and the other pointer starts from the meeting point. Each step, the two pointers will meet at the entry point.

struct ListNode *detectCycle(struct ListNode *head) {
    struct ListNode *fist=head,*slow=head;
    if(head==NULL||head->next==NULL){
        return NULL;
    }
    while(fist&&fist->next){
        fist=fist->next->next;
        slow=slow->next;
        //If you meet, let the fast pointer return to the starting point
        if(fist==slow){
            slow=head;
            //Meet again, the meeting point is the entry point
            while(slow!=fist){
                slow=slow->next;
                fist=fist->next;
            }
            return slow;
            break;
        }
    } 
    return NULL;
}

3. Force buckle 160: intersecting linked list

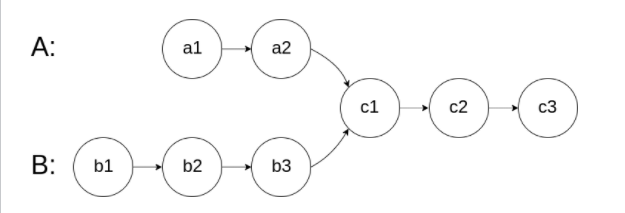
Here are the head nodes headA and headB of the two single linked lists. Please find and return the starting node where the two single linked lists intersect. If two linked lists do not have intersecting nodes, null is returned
It is shown that the two linked lists intersect at node c1, and the subject data ensures that there are no rings in the whole chain structure. Note that after the function returns the result, the linked list must maintain its original structure.
As shown in the figure, two linked lists intersect at node c1:

analysis:
What is intersection:

1. Use double pointers to solve the problem that pA traverses headA and passes it to headB, and pB traverses headB and passes it to headA. The two pointers will meet at the intersection

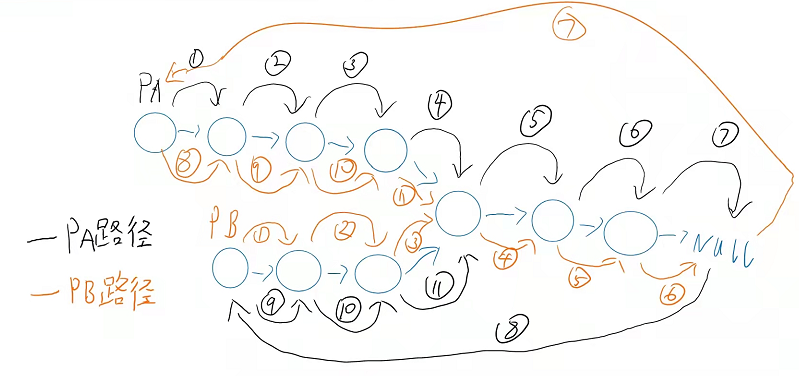
2. If there are two disjoint linked lists, pA and pB will traverse headA and headB at the same time and reach NULL

struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    struct ListNode* pA=headA;
    struct ListNode* pB=headB;
    if(headA==NULL||headB==NULL){
        return NULL;
    }
    while(pA!=pB){
        if(pA==NULL){
            pA=headB;
        }
        else{
            pA=pA->next;
        }
        if(pB==NULL){
            pB=headA;
        }
        else{
            pB=pB->next;
        }
        }
        return pA;
}

4. Force buckle 138: copy the linked list with random pointer

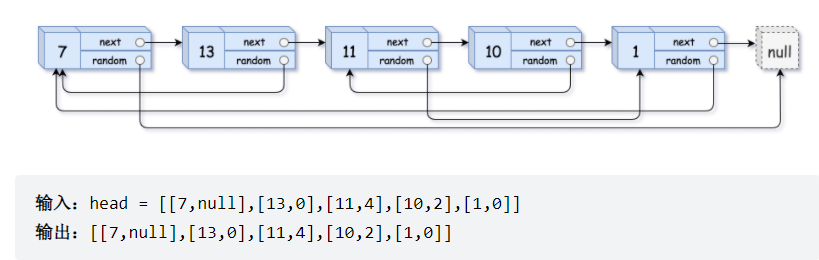
Give you a linked list with a length of N. each node contains an additional random pointer random, which can point to any node or empty node in the linked list. Construct a deep copy of this linked list. The deep copy should consist of exactly n new nodes, in which the value of each new node is set to the value of its corresponding original node. The next pointer and random pointer of the new node should also point to the new node in the replication linked list, and these pointers in the original linked list and the replication linked list can represent the same linked list state. The pointer in the copy linked list should not point to the node in the original linked list.
For example, if there are two nodes X and Y in the original linked list, where x.random -- > y. Then the corresponding two nodes X and Y in the copy linked list also have
x.random --> y .

Returns the header node of the copy linked list.

analysis:
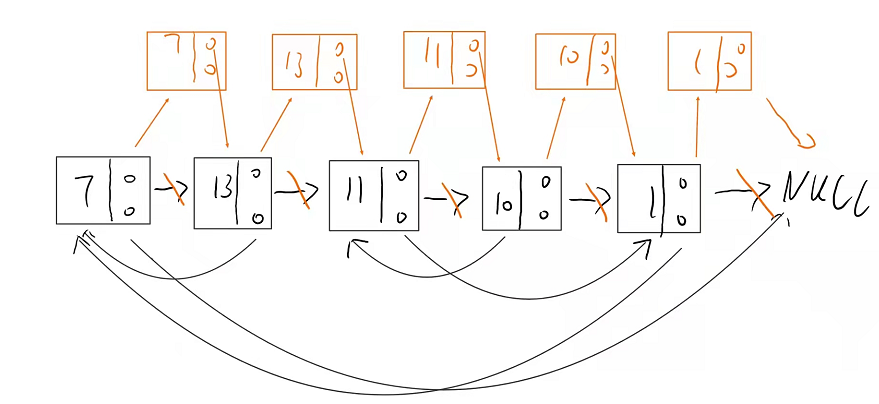
1. Step 1: copy the val field of the original linked list and insert it behind the original node
2. Step 2: copy the random domain of the original linked list
3. Split the linked list and restore the original linked list

struct Node* copyRandomList(struct Node* head) {
    struct Node* cur=head;
    //1. Copy the val field of the original node to the back of the original node
    while(cur){
        struct Node* newnode=(struct Node*)malloc(sizeof(struct Node));
        newnode->val=cur->val;

        newnode->next=cur->next;
        cur->next=newnode;
        cur=newnode->next;
    }
    //2. Copy the random domain of the node
    cur=head;
    while(cur){
        struct Node* prev=cur->next;
        if(cur->random==NULL){
        prev->random=NULL;
        }
        else{
        prev->random=cur->random->next;
        }
        cur=prev->next;
    }
     //3. Disconnect the linked list 
    struct Node* newhead=NULL;
    struct Node* tail=NULL;
    cur=head;
    while(cur){
        struct Node* copy=cur->next;
        struct Node* next=copy->next;
        if(tail==NULL){
            newhead=tail=copy;
        } 
        else{
            tail->next=copy;
            tail=copy;
        }
        cur->next=next;
        cur=next;
    }
    return newhead;
}