Summary of Data Structure Code Title

Title 01

A cyclic single-chain list with leading nodes whose node values are positive integers is designed. An algorithm is designed to repeatedly find the node with the lowest node value in the single-chain list and output it. Then the point is deleted from the single-chain list until the single-chain table is empty and the header node is deleted.

Topic Analysis

1. By analyzing the above meanings, the general solution process is as follows:

1. Find the minimum node that meets the requirements first
2. Delete
3. Attention!!!!!! The above two steps only delete a minimum node based on a single-chain list traversal
4. What the title requires is to repeatedly find the node with the smallest node value in the single-chain list, output it, and delete it, which requires another loop to traverse.

For how to find the minimum node of a single-chain list and delete the current minimum node, the links to the first topic in the previous article are as follows:
Find Delete Minimum Node

To facilitate comparison, the code operation design for finding and deleting minimum nodes in the previous article is as follows:

//It's necessary to add a sign because you want to manipulate a list of chains
//structural morphology
typedef struct LNode{
	int data;
	struct LNode *  next;
};

ListLink Delete_min(ListList &L){
	//Initialize Node
	LNode * pre = L;
	LNode * p = pre->next;//Next Node Pointing to Head Node
	LNode * minp = p;//min initialization
	LNode * minpre = pre;//Initialization Precursor

	while(p != null){
		//Core Code
		if(p->data < minp->data){
			minp = p;
			minpre = pre;
		}else{
			pre = p;
			p = p->next;
		}//Not the current minimum
		//Delete Find Nodes
		//A precursor to the minimum found
		minpre->next = minp->next;
		free(minp);
	}
}

Combining the above code snippets, we will complete the answer to the current topic.

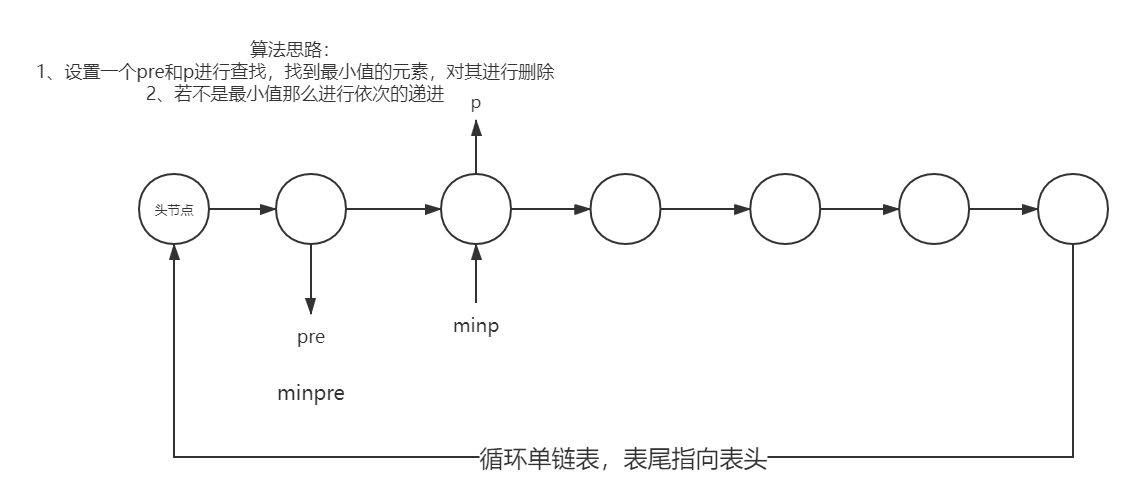
Since the title requires us to iteratively find deletable elements in a circular single-chain list, we need to apply an additional loop to them.
Ideas for implementation:

1. Set up a big loop first
2. Initialize related pointers in a loop
3. Include pre, p, minp, minpre pointer
4. Query
5. pre and p move backwards if they are not minimum
6. If so, delete it
7. Remove Head Node Last

The complete code is as follows:

typedef int ElemType;
//Set Structure
typedef struct LNode{
	ElemType data;
	struct LNode *next;
}LNode, *LinkList;

//Delete all elements that need to be deleted
void Delete_xAll(LinkList &L){
	while(L->next != L){//L->next!=L--This sentence represents the end of a loop single-chain table,
						//That is, the tail node points to the head node
		LNode* pre = L;
		LNode* p = L->next;
		LNode* minp = p;
		LNode* minpre = pre;//Initialization Action Pointer
		while(p!= L){//End Node Points to Head Node as Stop
			if(p->data < minp->data){
				minp = p;
				minpre = pre;
			}else{
				//No minimum found
				pre = p;
				p = p->next;
			}
			//Delete
			minpre->next = minp->next;
			free(minpre);
		}
	}
	//Delete the root node last
	free(L);
}

Comparing with the code above, one of the changes is that:

1,

	while(p!= L){//End Node Points to Head Node as Stop
			if(p->data < minp->data){
				minp = p;
				minpre = pre;
			}else{
				//No minimum found
				pre = p;
				p = p->next;
			}
		}

2,

while(L->next != L){//L->next!=L - - This sentence represents the end of a looping single-chain table, //that is, the trailing node points to the heading node`}

Answer complete!

Title 02

1. Title Analysis

1. First, the attributes of a node are original, pred, data, next become pred, next, data, freq for design
2. Secondly, the essence of what needs to be done according to the requirements of the title is
3. Sort freq in descending order by Locate function

2. Algorithmic ideas

1. Find the node containing x first, and add the freq realm data for that node+1
2. Remove the node from the list
3. Look forward to its precursor nodes.
4. Find the next element of an element larger than that node
5. Performs insert node operation of double-linked list.

Here is a step-by-step implementation of the complete code, starting with the core code:
1. Write the structure first, find the node containing x, and make freq+1;

typedef struct DNode
{
	ElemType data;
	struct LNode *pred,*next;
	ElemType freq;
}DNode,*DLinkList;
//Find Nodes
while(p!=NULL && p->data==x){
	p = p->next;
}

2. There are two conditions for the end of the search

1. P is null, because the loop jumps out to represent a node where the specified x is not found
2. p is not null, so the node whose value is x was found

3. Add 1 to its freq and take out its link list node.
The operation of its + 1 is not pasted here, and the link list node removal is illustrated:

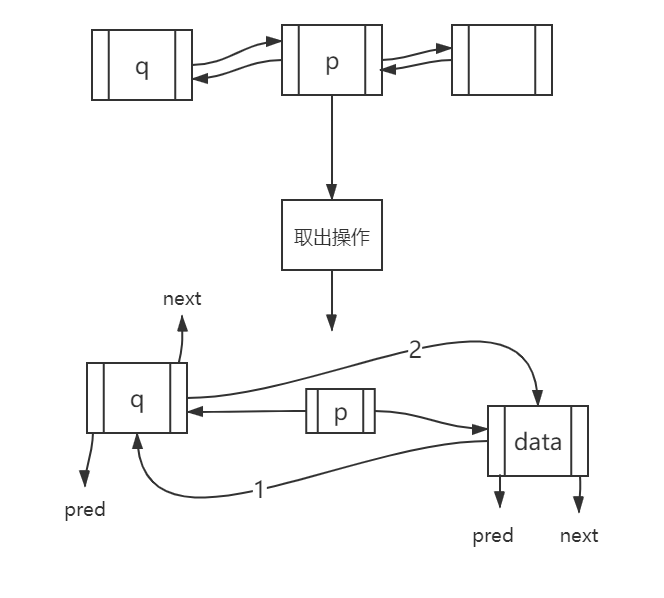
The code for implementation is as follows:

p->next->pred = p->pred;//Remove nodes as illustrated above
p->pred->next = p->next;

4. Traverse forward to find nodes until a node larger than node x is found and stop
Insert nodes.

The insertion code of the double-linked list is explained here:
Look at the picture first

The code for inserting the node is explained as follows:
Combined with the above step-by-step analysis, the complete code is as follows:

//structural morphology
typedef struct DNode
{
	ElemType data;
	struct LNode *pred,*next;
	ElemType freq;
}DNode,*DLinkList;

DLinkList Locate(DLinkList &L,ElemType x){
	LNode * p = L->next;
	LNode *q;//A pioneer representing p
	//lookup
	while(p!= NULL && p->data != x){
		p = p->next;
	}
	if(p== NULL){
		printf("%d\n", "Search failed");
		exit(-1);
	}else{
		//Find Successful
		p->freq++;
		//Remove Node
		p->next->pred = p->pred;
		p->pred->next = p->next;
		//Find the right place to insert
		q = p->pred;//Set the precursor of p to look for
		while(q != L && q->data <= p->data){
			q = q->pred;//Look Forward
		}
		//Find a suitable location for node insertion
		p->next = q->next;
		q->next->pred = p;
		p->pred = q;
		q->next = p;

	}
	return p;
}

Complete answer!!

Title 03
Given a single-chain list with a header node, design an algorithm that is as efficient as possible for time and space, find the value of the last k th node of the list, and print a return of 1 if no return of 0 is found

Title Analysis:

1. Regardless of time complexity, the length of a single-chain table is obtained by first traversing it, and the length-k value is accessed by second traversal.
2. Regardless of the concept of time complexity, the first traversal is stored in the array, and the second access to the length-k+1 location element of the array

However, the requirement is to consider time and space complexity, so neither of the above methods is applicable.

New ideas for algorithm

1. The k-th value of a positive number,
2. Find the tail pointer for interval movement

The code illustration for its implementation is as follows:

Its implementation ideas are:
P moves k units backwards, then p and q move back together until P is kong and reaches the end of the table, where q points to the last k node.

The complete code is as follows:

typedef int ElemType;
//Set Structure
typedef struct LNode{
	ElemType data;
	struct LNode *next;
}LNode, *LinkList;

//Core Code
int Search_x(LinkList list,ElemType k){
	LNode * p = list->next;
	LNode * q = list->next;
	int count = 0;//Set Count
	while(p!=NULL){
		if(count < k){
			count++;
			p =p->next;
		}else{
			p = p->next;
			q = q->next;//p arrives at the specified location and moves both p and q
		}
	}
	if(count<k){
		return 0;//Failed lookup
	}else{
		return 1;//Successful Find
	}
}

Algorithms learn to fuel!