Iterative method to realize the subsequent traversal of binary tree

1. Recursive version

public static void dfs(TreeNode root){
  	if(root==null){
        return;
    }
    if(root.left!=null)
    dfs(root.left);
    if(root.right!=null)
    dfs(root.right);
    System.out.println(root.val);
}

From the recursive version, we can see that we need to traverse all the left nodes in the first step
Here we use a stack to store the nodes of the tree to simulate recursive first in and last out.

Stack<TreeNode> stack = new Stack<>();
if(root!=null){
	return;
}
stack.push(root);
while(!stack.isEmpty()){
	//Traverse all left nodes until the left node is null
	while(root!=null&&root.left!=null){
		root = root.left;
		stack.push(root);
	}
	//The second step of recursion is to access the right subtree.
	root = stack.pop();  //Take out the top element of the stack and prepare to traverse its right subtree
	if(root.right==null){ //Note: if there is no right subtree, you can directly access the root node
		System.out.println(root.val);
	}else{
		//Then it will return to the while loop above to traverse all the left nodes of the right subtree
		root = root.right; 
		stack.push(root);
	}
}

The above is the general logic, but there are two important problems that have not been solved.
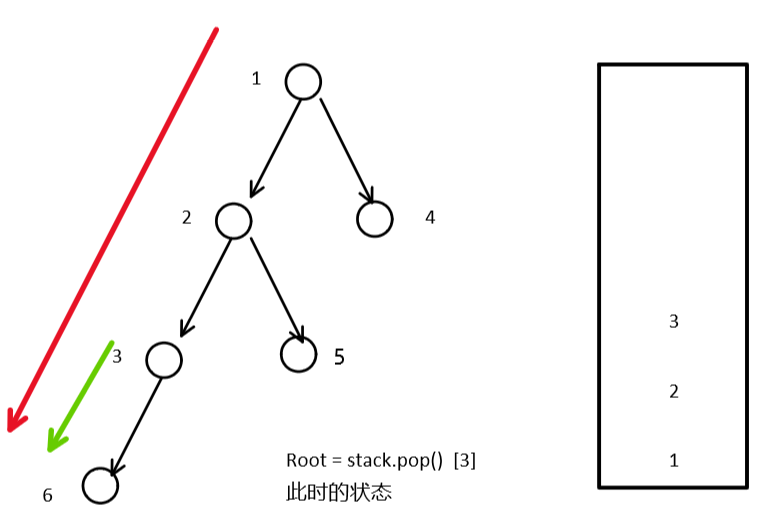
Question 1: about repeated access to the left subtree.
1. When the top node of the stack is 3, root = stack.pop(). At this point, root points to node 3

2. Then enter the while loop, and node 6 will be accessed again. Because node 1 has visited 6.

The red arrow indicates that for the root node, access to all left nodes of its left subtree.
The green arrow represents 3 nodes and accesses all left nodes of its left subtree. It can be seen that 6 nodes are accessed repeatedly.

Solution: set the node taken from the stack to null if there is no right subtree.

Stack<TreeNode> stack = new Stack<>();
if(root!=null){
	return;
}
stack.push(root);
while(!stack.isEmpty()){
	while(root!=null&&root.left!=null){
		root = root.left;
		stack.push(root);
	}
	root = stack.pop();  
	if(root.right==null){ 
		root = null;  //Prevent duplicate access to left node
		System.out.println(root.val);
	}else{
		root = root.right; 
		stack.push(root);
	}
}

Question 2:
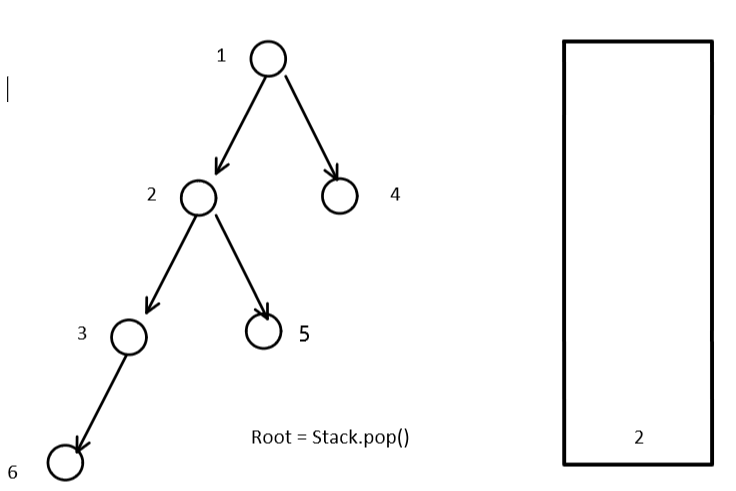
When the node taken out from the top of the stack has a right subtree, the node is not accessed.

while(!stack.isEmpty()){
	while(root!=null&&root.left!=null){
		root = root.left;
		stack.push(root);
	}
	root = stack.pop();  
	if(root.right==null){ 
		root = null;
		System.out.println(root.val);
	}else{  
		//With right subtree. At this time, root is not accessed, and root = root.right; It's covered. This will cause the current node root to lose access.
		root = root.right; 
		stack.push(root);
	}
}

Solution: save root back on the stack before root is overwritten by root = root.right.
The purpose of taking out root is to access its right subtree.

while(!stack.isEmpty()){
	while(root!=null&&root.left!=null){
		root = root.left;
		stack.push(root);
	}
	root = stack.pop();  
	if(root.right==null){ 
		root = null;
		System.out.println(root.val);
	}else{  
		stack.push(root); //Save current node
		root = root.right; 
		stack.push(root); //Save the right child node of the current node
	}
}

Although it solves the problem that the node is not accessed when the node taken out from the top of the stack has a right subtree, it leads to a new problem, repeated access to the right subtree.

In order to solve the problem of missing access, 2 nodes are stored on the stack twice.

1. Once, it is added by traversing all left sub nodes of all left sub trees. (the purpose of this addition is to traverse the right subtree of the node)

2. Once, in order to solve the missing access, 2 nodes are stored in the stack. (the purpose of this time is to access 2 nodes after traversing the right subtree, because it is post order traversal)

It can be seen from the code that if we do not restrict it, this 2 node will enter the z stack for the third and fourth time, resulting in repeated access.

Our requirement is to access nodes with right subtree only twice. So we can introduce a tag.
TreeNode pre = null
The pre variable is used to identify whether the right subtree of the node has been traversed, and if so. We won't put it on the stack again.
When pre==root.right, the right subtree has been accessed.

Final version

//This pre prevents repeated traversal of the right subtree
TreeNode pre = null;
 while(!stack.isEmpty()){
     while (root!=null&&root.left != null) {
         root = root.left;
         stack.push(root);
     }
     root = stack.pop();
     //pre==root.right
     if(root.right==null||pre==root.right){
         pre = root;
         System.out.println(root.val);
         //This root is set to null to prevent repeated traversal of the left subtree
         root = null;
     }else{
         stack.push(root);
         root = root.right;
         stack.push(root);
     }
 }

If the right subtree of node 2 is equal to pre, it means that the right subtree has been accessed. After the left and right subtrees of node 2 are accessed, you can continue to process node 1 according to the same operation.

As can be seen from the figure, the pre pointer is passed up step by step from bottom to top.