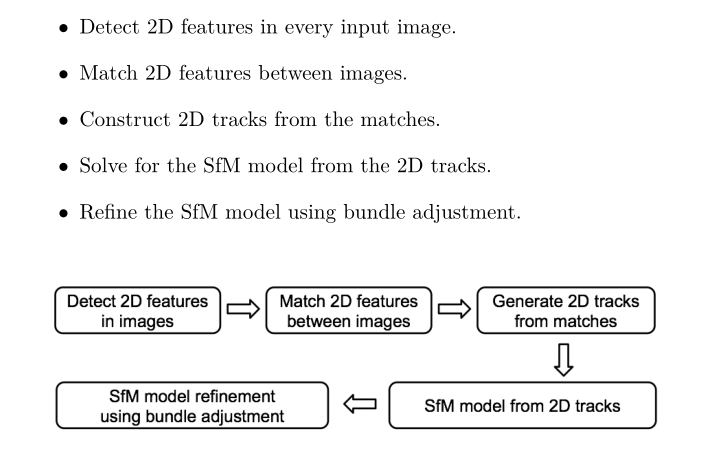
The first two steps of SFM algorithm: feature point extraction and matching. You can see my article: sift, surf, orb feature extraction - 3D reconstruction , the next three steps are mainly described in detail here.
This seems a little useful and can be used as a reference
3. Construct 2D tracks from the matches
After the matching relationship is established, a track list needs to be generated, which refers to the photo collection of points with the same name, such as the first picture
Point 13 of and point 14 of the second sheet and point 115 of the fifth sheet are points of the same name, then (1,13)
(2,14) and (5115) belong to a track. Based on this, a track set can be generated and generated at the same time
It is also necessary to eliminate useless matches when forming a track:
- If a track contains the same graph more than once, it should be rejected because there are many tracks in the same graph
If all feature points match the same point, the matching relationship must be wrong. - If there are too few track s, they should be eliminated. Generally, 2 (minimum value) is taken, which means that only two images have the same point, and there is too little information in 3D reconstruction, which is easy to produce errors.
4. Solve for the SfM model from the 2D tracks
Mathematical principles
-
The fourth step is to find the initial image pair. The purpose is to find the image pair with the largest camera baseline. The four point method of RANSC algorithm is used to calculate the homography matrix. The matching points that meet the homography matrix are called inner points, and those that do not meet the homography matrix are called outer points. According to the homography matrix formula, the smaller T (? What is this?), the higher the proportion of inner points, that is, the more obvious the phenomenon of low parallax. See the following for details: How much does harmony know?
Therefore, finding an image pair with the smallest proportion of interior points is the initialization image pair. Of course, its premise must meet the reconstruction, which can be guaranteed by the number of matching points. -
The fourth step is to initialize the relative orientation of the image pair. The eigenmatrix is calculated according to the RANSC eight point method. The R and T of the second image can be obtained by decomposing the eigenmatrix SVD. In this step, distortion correction is required, and then the three-dimensional points are calculated according to R, T and the corrected image point coordinate triangulation (what is coordinate triangulation? How to operate? See: triangulation for depth value (for three-dimensional coordinates)).
Code
from utils import *
import logging
class Baseline:
"""Represents the functions that compute the baseline pose from the initial images of a reconstruction"""
def __init__(self, view1, view2, match_object):
self.view1 = view1 # first view
self.view1.R = np.eye(3, 3) # identity rotation since the first view is said to be at the origin
'''
array([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
'''
self.view2 = view2 # second view
self.match_object = match_object # match object between first and second view
def get_pose(self, K):
"""Computes and returns the rotation and translation components for the second view"""
F = remove_outliers_using_F(self.view1, self.view2, self.match_object)#return fundamental matrix
E = K.T @ F @ K # compute the essential matrix from the fundamental matrix
#E: How does the essential matrix change from F to e? K is the intrinsic matrix
#Functions of @ in python: 1. Decorator 2. Matrix multiplication
logging.info("Computed essential matrix")
logging.info("Choosing correct pose out of 4 solutions")
return self.check_pose(E, K)
def check_pose(self, E, K):
"""Retrieves the rotation and translation components from the essential matrix by decomposing it and verifying the validity of the 4 possible solutions"""
R1, R2, t1, t2 = get_camera_from_E(E) # decompose E
#Recovering camera parameter matrix from essential matrix
if not check_determinant(R1):
R1, R2, t1, t2 = get_camera_from_E(-E) # change sign of E if R1 fails the determinant test
#?
# solution 1
reprojection_error, points_3D = self.triangulate(K, R1, t1)#Filter mismatch
#
# check if reprojection is not faulty and if the points are correctly triangulated in the front of the camera
if reprojection_error > 100.0 or not check_triangulation(points_3D, np.hstack((R1, t1))):
# solution 2
reprojection_error, points_3D = self.triangulate(K, R1, t2)
if reprojection_error > 100.0 or not check_triangulation(points_3D, np.hstack((R1, t2))):
# solution 3
reprojection_error, points_3D = self.triangulate(K, R2, t1)
if reprojection_error > 100.0 or not check_triangulation(points_3D, np.hstack((R2, t1))):
# solution 4
return R2, t2
else:
return R2, t1
else:
return R1, t2
else:
return R1, t1
def triangulate(self, K, R, t):
"""Triangulate points between the baseline views and calculates the mean reprojection error of the triangulation"""
K_inv = np.linalg.inv(K)
P1 = np.hstack((self.view1.R, self.view1.t))
P2 = np.hstack((R, t))#From the decomposition of the essential matrix
# only reconstructs the inlier points filtered using the fundamental matrix
pixel_points1, pixel_points2 = get_keypoints_from_indices(keypoints1=self.view1.keypoints,
keypoints2=self.view2.keypoints,
index_list1=self.match_object.inliers1,
index_list2=self.match_object.inliers2)
# convert 2D pixel points to homogeneous coordinates
pixel_points1 = cv2.convertPointsToHomogeneous(pixel_points1)[:, 0, :]#convertPointsToHomogeneous transforms points from European space to homogeneous space,
pixel_points2 = cv2.convertPointsToHomogeneous(pixel_points2)[:, 0, :]
reprojection_error = []
points_3D = np.zeros((0, 3)) # stores the triangulated points
for i in range(len(pixel_points1)):
u1 = pixel_points1[i, :]
u2 = pixel_points2[i, :]
# convert homogeneous 2D points to normalized device coordinates
#The operation with the internal parameter matrix is called normalized
u1_normalized = K_inv.dot(u1)
u2_normalized = K_inv.dot(u2)
# calculate 3D point
point_3D = get_3D_point(u1_normalized, P1, u2_normalized, P2)
# calculate reprojection error
error = calculate_reprojection_error(point_3D, u2[0:2], K, R, t)#Reconstruction error
reprojection_error.append(error)
# append point
points_3D = np.concatenate((points_3D, point_3D.T), axis=0)
return np.mean(reprojection_error), points_3D
5.Refine the SfM model using bundle adjustment
- Add more images. Take the third graph as an example. According to the three-dimensional points generated in step 4 and the track relationship between the third graph and the first two graphs, the R and T of the third graph can be inversely calculated, and then continue to triangulate
More three-dimensional points. Repeat step 5 repeatedly. Finally, the POSE (R, T) and three-dimensional points of all photos will be obtained, which is the result of sparse reconstruction SFM. - From the fourth step, Bundle+Adjustment of beam method adjustment is a nonlinear optimization process. The purpose is to minimize the reconstruction error and minimize the back projection difference by adjusting POSE and three-dimensional points. If the camera is not calibrated, the focal length should also be involved in the adjustment.
- Bundle+Adjustment is an iterative process. After one iteration, all three-dimensional points are backprojected to the pixel coordinates of their photos and compared with the initial coordinates respectively. If they are greater than a certain threshold, they should be removed from the track. If they are less than 2 in the track, the whole track will be removed and optimized until there are no points to go
Full reference code: structure-from-motion