Suffix Array S A \tt SA SA can be used in all aspects of string problems. Its purpose is to find the ranking of all suffixes of this string in dictionary order.

Pre knowledge

Multiplier / DC3

Algorithm usage

It can be used to find the longest common substring, the longest palindrome string, etc

Algorithm complexity

String length is n \tt n n

time

O ( n log ⁡ n ) \tt O(n\log n) O(nlogn)

space

O ( n ) \tt O(n) O(n)

Algorithm implementation

You know, the most violent algorithm is to find all suffixes and use them s o r t \tt sort Sort sort

Although the time complexity is the same as this algorithm O ( n log ⁡ n ) \tt O(n\log n) O(nlogn), but the space of this algorithm is O ( n 2 ) \tt O(n^2) O(n2). It explodes easily.

Suffix array requires two arrays: suffix array S A \tt SA SA and rank array r a n k \tt rank rank

S A i \tt SA_i SAi # represents i \tt i Ranking of suffixes starting with i characters.

r a n k i \tt rank_i ranki's representative is ranked as i \tt i The subscript of the beginning character of the suffix of i.

So, actually S A i = j \tt SA_i = j When SAi = j, r a n k j = i \tt rank_j = i rankj​=i.

For the implementation of suffix array, there are two main algorithms:

• Doubling Algorithm

• DC3 algorithm

I only talk about multiplication here (mainly DC3, I won't).

The multiplication algorithm is mainly recursive,

We first find out the order of each suffix according to the first character r a n k \tt rank rank (if the same ranking is the same),

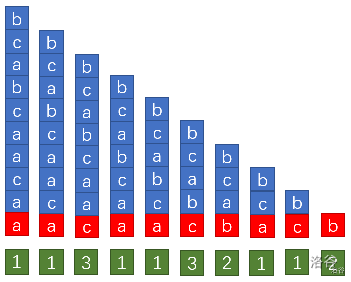
Then use this to deduce all suffixes sorted according to the first two characters r a n k \tt rank rank，

Then four, eight

Because before calculating all suffixes 2 k \tt 2^k 2k character sorted r a n k \tt rank rank, because we have found that according to the previous 2 k − 1 \tt 2^{k-1} 2k − 1 sorted r a n k \tt rank rank's.

So we can put this before 2 k \tt 2^k 2k characters, divided into [ 1 , 2 k − 1 ] \tt [1, 2 ^ {k-1}] [1,2k − 1] and [ 2 k − 1 + 1 , 2 k ] [\tt 2^{k - 1} + 1, 2 ^k] [2K − 1+1,2k] two parts

Namely r a n k [ i ] \tt rank[i] rank[i] and r a n k [ i + 2 k − 1 ] \tt rank[i + 2^{k - 1}] rank[i+2k − 1] (when we find that there is no one in the back, take it 0 \tt 0 0 instead).

We found that we both know their r a n k \tt rank rank, we just need to take these two r a n k \tt rank rank is combined into a two tuple, and then all the two tuples are arranged in order.

Repeat this step until all r a n k \tt rank Until rank is different. And then I figured it out r a n k \tt rank rank is the ranking array we require.

At this time, we need $\ tt \log n $times at most r a n k \tt rank rank, every time you need O ( n log ⁡ n ) \tt O(n\log n) O(nlogn), so the total time complexity is O ( n log ⁡ 2 n ) \tt O(n\log^2n) O(nlog2n).

Tree array has another basic operation. We can quickly find the length of the longest prefix of two adjacent strings after sorting.

We let l e n g t h i \tt length_i lengthi represents S A [ i ] \tt SA[i] SA[i] and S A [ i + 1 ] \tt SA[i + 1] Length of longest prefix of SA[i+1]

Algorithm application

Longest common substring

Longest Common Prefix

Algorithm optimization

1. Cardinality sorting optimization

We know, because r a n k \tt rank The number in the rank array must be [ 1 , n ] \tt [1, n] [1,n], so we can use cardinal sort instead of quick sort.

For binary cardinality sorting, we need to first put the second keyword into the bucket, then enumerate each bucket from small to large, and take out the numbers in the bucket one by one according to the order in which they are put,

Then put the first keyword in and take it out, and the resulting array is in good order.

So the complexity of this sorting algorithm is O ( n ) \tt O(n) O(n), so the time complexity after optimization is O ( n log ⁡ n ) \tt O(n\log n) O(nlogn)

code

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
char str[100010];
int cnt[100010];
int rk[100010];
int y[100010];
int SA[100010];
int height[100010];
int n, m;
int get_SA()
{
	for(int i = 1; i <= n; i++)
	{
		rk[i] = str[i];
		cnt[rk[i]]++;
	}
	for(int i = 2; i <= m; i++)
	{
		cnt[i] += cnt[i - 1]; 
	}
	for(int i = n; i >= 1; i--)
	{
		SA[cnt[rk[i]]--] = i; 
	}
	for(int k = 1; k <= n; k <<= 1)
	{
		int num = 0;
		for(int i = n - k + 1; i <= n; i++)
		{
			y[++num] = i;
		}
		for(int i = 1; i <= n; i++)
		{
			if(SA[i] > k)
			{
				y[++num] = SA[i] - k;
			}
		}
		for(int i = 1; i <= m; i++)
		{
			cnt[i] = 0;
		}
		for(int i = 1; i <= n; i++)
		{
			cnt[rk[i]]++;
		}
		for(int i = 2; i <= m; i++)
		{
			cnt[i] += cnt[i - 1];
		}
		for(int i = n; i >= 1; i--)
		{
			SA[cnt[rk[y[i]]]--] = y[i];
			y[i] = 0;
		}
		swap(rk, y);
		rk[SA[1]] = 1;
		num = 1;
		for(int i = 2; i <= n; i++)
		{
			if(y[SA[i]] == y[SA[i - 1]] && y[SA[i] + k] == y[SA[i - 1] + k])
			{
				rk[SA[i]] = num;
			}
			else
			{
				rk[SA[i]] = ++num;
			}
		}
		if (num == n)
		{
			break;
		}
		m = num;
	}
	for(int i = 1; i <= n; i++)
	{
		printf("%d ", rk[i]);
	}
	printf("\n");
}

void get_height()
{
	for(int i = 1; i <= n; i++)
	{
		rk[SA[i]] = i;
	}
	int k = 0;
	for(int i = 1; i <= n; i++)
	{
		if(k)
		{
			k--;
		}
		int j = SA[rk[i] - 1];
		while(str[i + k] == str[j + k])
		{
			k++;
		}
		height[rk[i]] = k;
	}
	for(int i = 1; i <= n; i++)
	{
		printf("%d ", height[i]);
	}
	printf("\n");
}

int main()
{
	scanf("%s", str + 1);
	n = strlen(str + 1);
	m = 256;
	get_SA();
	get_height();
	return 0;
}