streamgame1 of attack and defense world crypto master problem

Continue to start the reverse journey of the whole stack of dreams~
This problem is streamgame1 of the world's crypto master problem

.
.
Download attachments, which are typical LFSR types:

from flag import flag
assert flag.startswith("flag{")
# Function: judge whether the string starts with the specified character or substring flag{
assert flag.endswith("}")
# Function: judge whether the string ends with the specified character or substring}, flag {}, 6 bytes
assert len(flag)==25
# The length of the flag is 25 bytes, 25-6 = 19 bytes
#3 < < 2 can be calculated as follows: bin(3)=0b11 moves 2 bits to the left to become 1100, 0b1100 = 12 (decimal)
def lfsr(R,mask):
    output = (R << 1) & 0xffffff    #Move R to the left by 1 bit, bin (0xFFFFFF) ='0b111111111111 '= binary complement of 0xFFFFFF
    i=(R&mask)&0xffffff             #Bitwise and operator &: two values participating in the operation. If both corresponding bits are 1, the result of this bit is 1, otherwise it is 0
    lastbit=0
    while i!=0:
        lastbit^=(i&1)    #Bitwise exclusive or operator: when two corresponding binary bits are different, the result is 1
        i=i>>1
    output^=lastbit
    return (output,lastbit)



R=int(flag[5:-1],2)
mask    =   0b1010011000100011100

f=open("key","ab")   #Open in binary append mode
for i in range(12):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out   #Bitwise exclusive or operator: when two corresponding binary bits are different, the result is 1
    f.write(chr(tmp))  #chr() takes an integer in the range (256) (i.e. 0 ~ 255) as a parameter and returns a corresponding character.
f.close()

.
.
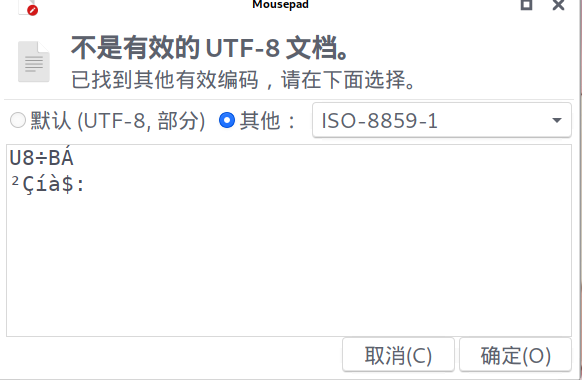
The plaintext key is as follows, which needs to be converted to a flag that can deduce the corresponding digits of the initial state value (flag):

.
.
(first experience here)
LFSR type I'm on the blog https://blog.csdn.net/xiao__1bai/article/details/120392307 has been summarized, so here you can directly apply the previous summary steps and follow them:

.
.
(second experience here)
The key is how to get the key value. At first, I directly copy and paste characters to hexadecimal, and then take the first 19 digits. It can be imagined that of course it is wrong.

Then I checked many materials and sent some codes that they read binary numbers from files. It was not easy enough, so I absorbed the code encoded by base64 and wrote a string of aligned binary codes from files, which can be used directly in the future.
(in online conversion, the first 0 will be omitted, resulting in the wrong number of result digits, which will lead to the wrong result, so you should pay attention to yourself.)

f = open('5key','rb')	#Open file in binary format
content = f.read()		#Hex of type \ xhh was read
#print(content)
key=['{:0>8}'.format(str(bin(i)).replace('0b','')) for i in content]	#Lessons learned from base64 coding, binary 8-bit alignment.
print(''.join(key)[:19])

.
.
The final problem-solving script is the same. Pay attention to the small end order:

f = open('5key','rb')	#Open file in binary format
content = f.read()		#Hex of type \ xhh was read
key=['{:0>8}'.format(str(bin(i)).replace('0b','')) for i in content]	#Lessons learned from base64 coding, binary 8-bit alignment.
key1=''.join(key)[:19]	#All lastbit values are the values generated by the feedback function, 32-bit key1
key2=key1
flag=[]
for i in range(19):
	output='?'+key1[:18]	#? 01000001111101110111011111000, because key1=str(lastbit)+key1[:31], key1 keeps filling, and output keeps taking the first 31 bits, so the output here sets "1" every time? Set it at bit i. note that output and key1 are independent and separate.
	flag.append(str(int(key2[-1-i])^int(output[-3])^int(output[-4])^int(output[-5])^int(output[-9])^int(output[-13])^int(output[-14])^int(output[-17])))
#The reason why we take negative numbers here is that we intercept from left to right, and in the computer, it is the small end order, which should be taken from right to left. key2[-1-i] here is the ith bit from left to right of the small end, that is, the ith bit of the generated value of the feedback function analyzed above. The original i-th bit of the flag value is now in the 19th bit, which can be obtained through the reversibility of ⊕ R19=lastbit ⊕ R3 ⊕ R4 ⊕ R5 ⊕ R9 ⊕ R13 ⊕ R14 ⊕ R17                    				
	key1=str(flag[i])+key1[:18]#Keep filling key1 and push key1 to the right,
print("flag{"+bin(int(''.join(flag[::-1]),2)).replace('0b','')+"}")#Here, after a series of operations, first change the flag to small end order [:: - 1], and then to hexadecimal.

.
.
result:

.
.
.
Summary:

1: (first experience here)
LFSR type I'm on the blog https://blog.csdn.net/xiao__1bai/article/details/120392307 has been summarized, so here you can directly apply the previous summary steps and follow them:

2:
(second experience here)
The key is how to get the key value. At first, I directly copy and paste characters to hexadecimal, and then take the first 19 digits. It can be imagined that of course it is wrong.
.
Then I checked many materials and sent some codes that they read binary numbers from files. It was not easy enough, so I absorbed the code encoded by base64 and wrote a string of aligned binary codes from files, which can be used directly in the future.
(in online conversion, the first 0 will be omitted, resulting in the wrong number of result digits, which will lead to the wrong result, so you should pay attention to yourself.)

f = open('5key','rb')	#Open file in binary format
content = f.read()		#Hex of type \ xhh was read
#print(content)
key=['{:0>8}'.format(str(bin(i)).replace('0b','')) for i in content]	#Lessons learned from base64 coding, binary 8-bit alignment.
print(''.join(key)[:19])

Finish it! Salute!