1. Introduction to Stack

The stack is an ordered list of FILO:First In Last Out.

Stack is a special linear table that limits the insertion and deletion of elements in a linear table to only occur at the same end.

One end that allows insertion and deletion is called the top of the stack and the other end is the fixed end, called the bottom of the stack.

Depending on the definition of the stack, elements first placed on the stack are at the bottom of the stack, and elements last placed on the top of the stack

Deleting an element is the opposite. The last element put in is deleted first, the first element put in is deleted last

2. Stack illustration

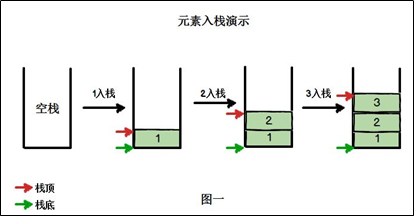
3. Stack out illustration

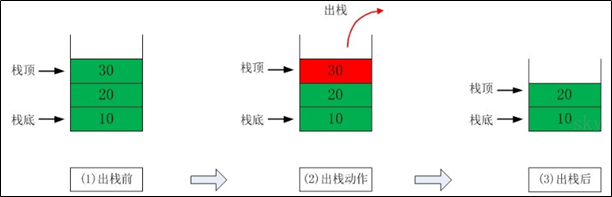
4. Scenarios

1) Call of a subprogram: Before jumping to a subprogram, the address of the next instruction will be stored on the stack until the subprogram is executed before taking out the address to return to the original program.

2) Processing recursive calls: Similar to the call of a subroutine, except that in addition to the address where the next instruction is stored, data such as parameters, region variables, and so on are stored on the stack.

3) Conversion of expression [suffix expression to suffix expression] and evaluation (actual solution).

4) Traversal of binary trees.

5) Graphic depth-first search method.

5. Simulate stack with array

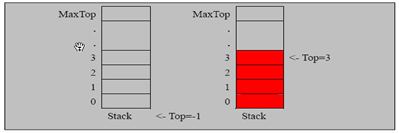
Ideas:

1) Define a top to represent the top of the stack, initialized to -1

2) stacking operation, when data is added to the stack, top+; stack[top] = data;

3) Out of stack operation, int value = stack[top]; top--; return value;

Code implementation:

//Define a ArrayStack Representation stack
class ArrayStack {
    private int maxSize; // Stack size
    private int[] stack; // Array, array simulation stack, where the data is placed
    private int top = -1;// top Represents the top of the stack, initialized to-1
    
    //constructor
    public ArrayStack(int maxSize) {
        this.maxSize = maxSize;
        stack = new int[this.maxSize];
    }
    
    //Full stack
    public boolean isFull() {
        return top == maxSize - 1;
    }
    //Stack empty
    public boolean isEmpty() {
        return top == -1;
    }
    //Push-push
    public void push(int value) {
        //First determine if the stack is full
        if(isFull()) {
            System.out.println("Full stack");
            return;
        }
        top++;
        stack[top] = value;
    }
    //Stack Out-pop, Return data from top of stack
    public int pop() {
        //First determine if the stack is empty
        if(isEmpty()) {
            //throw
            throw new RuntimeException("Stack empty, no data~");
        }
        int value = stack[top];
        top--;
        return value;
    }
    //Show the stack[Traverse Stack]， During traversal, data needs to be displayed from the top of the stack
    public void list() {
        if(isEmpty()) {
            System.out.println("Stack empty, no data~~");
            return;
        }
        //Data needs to be displayed from the top of the stack
        for(int i = top; i >= 0 ; i--) {
            System.out.printf("stack[%d]=%d\n", i, stack[i]);
        }
    }
}

6. Stack implements infix expression evaluator

Infix expressions are common operations, such as (3+4) *5-6

public class Calculator {

    public static void main(String[] args) {
        //Complete the expression according to the previous teacher's ideas
        String expression = "7*2*2-5+1-5+3-4"; // 15//How to deal with multidigit problems?
        //Create two stacks, a number stack, a symbol stack
        ArrayStack2 numStack = new ArrayStack2(10);
        ArrayStack2 operStack = new ArrayStack2(10);
        //Define the required related variables
        int index = 0;//For Scanning
        int num1 = 0; 
        int num2 = 0;
        int oper = 0;
        int res = 0;
        char ch = ' '; //Get every scan char Save to ch
        String keepNum = ""; //For splicing multiple digits
        //start while Cyclic Scan expression
        while(true) {
            //Get in turn expression Every character
            ch = expression.substring(index, index+1).charAt(0);
            //judge ch What is, and then do the appropriate processing
            if(operStack.isOper(ch)) {//If it is an operator
                //Determine if the current symbol stack is empty
                if(!operStack.isEmpty()) {
                    //Compare if symbol stack has operators,If the priority of the current operator is less than or equal to the operator in the stack,From the stack of numbers pop Out two numbers,
                    //In From Symbol Stack pop Out a symbol, perform the operation, and the result is put on the stack of numbers, then the current operator is put on the stack of symbols
                    if(operStack.priority(ch) <= operStack.priority(operStack.peek())) {
                        num1 = numStack.pop();
                        num2 = numStack.pop();
                        oper = operStack.pop();
                        res = numStack.cal(num1, num2, oper);
                        //The result of an operation is like a stack of numbers
                        numStack.push(res);
                        //Then put the current operator on the symbol stack
                        operStack.push(ch);
                    } else {
                        //If the priority of the current operator is greater than that of the operator in the stack, it goes directly to the symbol stack.
                        operStack.push(ch);
                    }
                }else {
                    //If empty, go directly to the symbol stack..
                    operStack.push(ch); // 1 + 3
                }
            } else { //If it is a number, go directly to the number stack
                
                //numStack.push(ch - 48); //? "1+3" '1' => 1
                //Analysis ideas
                //1. When dealing with multidigits, you can't find a number and immediately stack it because it may be multidigits
                //2. In the number of processes, you need to expression Expressive index See one more later,Scan for numbers and stack for symbols
                //3. So we need to define a variable string for splicing
                
                //Processing multi-digit
                keepNum += ch;
                
                //If ch Already expression The last one, go directly to the stack
                if (index == expression.length() - 1) {
                    numStack.push(Integer.parseInt(keepNum));
                }else{
                
                    //Determines whether the next character is a number, continues scanning if it is a number, and stacks if it is an operator
                    //Notice that the latter one, not the other index++
                    if (operStack.isOper(expression.substring(index+1,index+2).charAt(0))) {
                        //If the latter bit is an operator, stack keepNum = "1" perhaps "123"
                        numStack.push(Integer.parseInt(keepNum));
                        //Important!!!!!!, keepNum empty
                        keepNum = "";
                        
                    }
                }
            }
            //Give Way index + 1, And determine whether to scan to expression Last.
            index++;
            if (index >= expression.length()) {
                break;
            }
        }
        
        //When the expression is scanned, the order is from the stack of numbers and symbols pop Number and symbol, and run.
        while(true) {
            //If the symbol stack is empty, the final result is calculated, There is only one number in the stack [Result]
            if(operStack.isEmpty()) {
                break;
            }
            num1 = numStack.pop();
            num2 = numStack.pop();
            oper = operStack.pop();
            res = numStack.cal(num1, num2, oper);
            numStack.push(res);//Push
        }
        //The last number of stacks, pop Out is the result
        int res2 = numStack.pop();
        System.out.printf("Expression %s = %d", expression, res2);
    }

}

//Create a stack first,Create directly using the previous
//Define a ArrayStack2 Representation stack, Require extended functionality
class ArrayStack2 {
    private int maxSize; // Stack size
    private int[] stack; // Array, array simulation stack, where the data is placed
    private int top = -1;// top Represents the top of the stack, initialized to-1
    
    //constructor
    public ArrayStack2(int maxSize) {
        this.maxSize = maxSize;
        stack = new int[this.maxSize];
    }
    
    //Add a method that returns the value at the top of the current stack, But it's not real pop
    public int peek() {
        return stack[top];
    }
    
    //Full stack
    public boolean isFull() {
        return top == maxSize - 1;
    }
    //Stack empty
    public boolean isEmpty() {
        return top == -1;
    }
    //Push-push
    public void push(int value) {
        //First determine if the stack is full
        if(isFull()) {
            System.out.println("Full stack");
            return;
        }
        top++;
        stack[top] = value;
    }
    //Stack Out-pop, Return data from top of stack
    public int pop() {
        //First determine if the stack is empty
        if(isEmpty()) {
            //throw
            throw new RuntimeException("Stack empty, no data~");
        }
        int value = stack[top];
        top--;
        return value;
    }
    //Show the stack[Traverse Stack]， During traversal, data needs to be displayed from the top of the stack
    public void list() {
        if(isEmpty()) {
            System.out.println("Stack empty, no data~~");
            return;
        }
        //Data needs to be displayed from the top of the stack
        for(int i = top; i >= 0 ; i--) {
            System.out.printf("stack[%d]=%d\n", i, stack[i]);
        }
    }
    //Returns the priority of the operator, which is determined by the programmer, Priorities are represented by numbers
    //The larger the number, the higher the priority.
    public int priority(int oper) {
        if(oper == '*' || oper == '/'){
            return 1;
        } else if (oper == '+' || oper == '-') {
            return 0;
        } else {
            return -1; // Assume that the current expression only has +, - , * , /
        }
    }
    //Determine if it is an operator
    public boolean isOper(char val) {
        return val == '+' || val == '-' || val == '*' || val == '/';
    }
    //computing method
    public int cal(int num1, int num2, int oper) {
        int res = 0; // res Used to store the results of calculations
        switch (oper) {
        case '+':
            res = num1 + num2;
            break;
        case '-':
            res = num2 - num1;// Attention order
            break;
        case '*':
            res = num1 * num2;
            break;
        case '/':
            res = num2 / num1;
            break;
        default:
            break;
        }
        return res;
    }
}

7. Stack implementation suffix expression (inverse Poland) calculator

The evaluation of a suffix expression is the most familiar to us, but it is not easy for a computer to operate on. Therefore, when calculating the result, the suffix expression will often be converted to another expression to operate on (usually to a suffix expression)

A suffix expression, also known as an inverse Polish expression, is similar to a prefix expression except that the operator follows the operand, for example: (3+4)*5-6 The corresponding suffix expression is 34+5*6-

Another example is:

1) Computer evaluation of suffix expressions

Scan the expression from left to right, push the number into the stack when it encounters a number, pop up two numbers at the top of the stack when it encounters an operator, calculate them accordingly with the operator (the next top element and the top element of the stack), and put the result on the stack; repeat the process until the rightmost end of the expression, and the final value is the expressionResult of formula

For example, (3+4)*5-6 corresponds to a suffix expression of 34+5*6 -, and the evaluation steps for the suffix expression are as follows:

code implementation

//Complete the operation of the inverse Polish expression
/*
 * 1)Scan from left to right to push 3 and 4 onto the stack;
    2)Encountered the + operator, so pop up 4 and 3 (4 is the top element, 3 is the second top element), calculate the value of 3+4, get 7, and put 7 on the stack;
    3)Put 5 on the stack;
    4)Next is the * operator, so pop up 5 and 7, calculate 7 * 5 = 35, put 35 on the stack;
    5)Put 6 on the stack;
    6)The final result is the -operator, which calculates the value of 35-6, or 29.
 */
public static int calculate(List<String> ls) {
    // Create to Stack, Just one stack is needed
    Stack<String> stack = new Stack<String>();
    // ergodic ls
    for (String item : ls) {
        // Use regular expressions to take out numbers here
        if (item.matches("\\d+")) { // Multiple digits matched
            // Push
            stack.push(item);
        } else {
            // pop Out two numbers, combine them, and put them on the stack
            int num2 = Integer.parseInt(stack.pop());
            int num1 = Integer.parseInt(stack.pop());
            int res = 0;
            if (item.equals("+")) {
                res = num1 + num2;
            } else if (item.equals("-")) {
                res = num1 - num2;
            } else if (item.equals("*")) {
                res = num1 * num2;
            } else if (item.equals("/")) {
                res = num1 / num2;
            } else {
                throw new RuntimeException("Error in operator");
            }
            //hold res Push
            stack.push("" + res);
        }
    }
    //Last stayed stack The data in is the result of the operation
    return Integer.parseInt(stack.pop());
}

2) Infix expression to suffix expression

The steps are as follows:

For example, the process of converting the infix expression "1+((2+3)*4) -5" to a suffix expression is as follows:

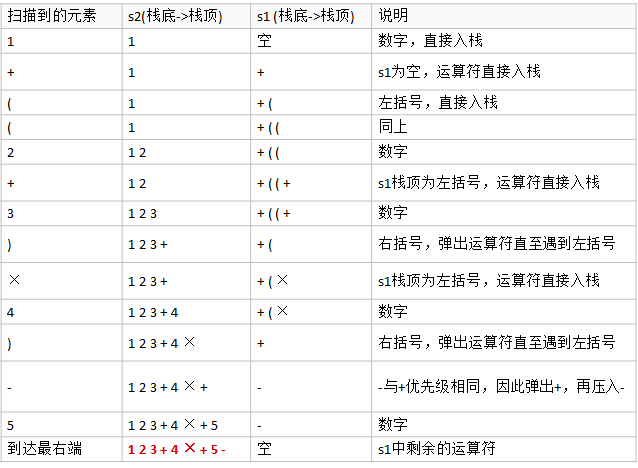
Code implementation:

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class PolandNotation {

    public static void main(String[] args) {
        
        
        //Completes the function of converting a suffix expression to a suffix expression
        //Explain
        //1. 1+((2+3)×4)-5 => Convert to 1 2 3 + 4 × + 5 –
        //2. Because it's directly against str The operation is inconvenient, so the first step is to  "1+((2+3)×4)-5" => The expression corresponding to the infix List
        //   That is "1+((2+3)×4)-5" => ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
        //3. Corresponds to the resulting infix expression List => Corresponding to the suffix expression List
        //   That is ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]  => ArrayList [1,2,3,+,4,*,+,5,–]
        
        String expression = "1+((2+3)*4)-5";//Notice the expression 
        List<String> infixExpressionList = toInfixExpressionList(expression);
        System.out.println("Corresponding to infix expression List=" + infixExpressionList); // ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]
        List<String> suffixExpreesionList = parseSuffixExpreesionList(infixExpressionList);
        System.out.println("Corresponding to the suffix expression List" + suffixExpreesionList); //ArrayList [1,2,3,+,4,*,+,5,–] 
        
        System.out.printf("expression=%d", calculate(suffixExpreesionList)); // ?
        
        /*
        
        //Define first to the inverse Polish expression
        //(30+4)×5-6  => 30 4 + 5 × 6 - => 164
        // 4 * 5 - 8 + 60 + 8 / 2 => 4 5 * 8 - 60 + 8 2 / + 
        //test 
        //Explain that for convenience, the numbers and symbols of the inverse Polish expression are separated by spaces
        //String suffixExpression = "30 4 + 5 * 6 -";
        String suffixExpression = "4 5 * 8 - 60 + 8 2 / +"; // 76
        //thinking
        //1. Put "34 + 5 x 6 -" => in ArrayList first
        //2. Pass an ArrayList to a method, traverse the ArrayList with the stack to complete the calculation
        
        List<String> list = getListString(suffixExpression);
        System.out.println("rpnList=" + list);
        int res = calculate(list);
        System.out.println("The result of the calculation is = "+ res";
        
        */
    }
    
    //That is ArrayList [1,+,(,(,2,+,3,),*,4,),-,5]  => ArrayList [1,2,3,+,4,*,+,5,–]
    //Method: The resulting infix expression corresponds to the List => Corresponding to the suffix expression List
    public static List<String> parseSuffixExpreesionList(List<String> ls) {
        //Define two stacks
        Stack<String> s1 = new Stack<String>(); // Symbol stack
        //Description: Because s2 This stack, during the entire conversion process, does not have pop Operation, and we need to reverse the order later
        //So it's cumbersome, we don't need it here Stack<String> Direct use List<String> s2
        //Stack<String> s2 = new Stack<String>(); // Stack for storing intermediate results s2
        List<String> s2 = new ArrayList<String>(); // Storing intermediate results Lists2
        
        //ergodic ls
        for(String item: ls) {
            //If it's a number, join s2
            if(item.matches("\\d+")) {
                s2.add(item);
            } else if (item.equals("(")) {
                s1.push(item);
            } else if (item.equals(")")) {
                //If it is a right parenthesis)"，Pop-up in turn s1 Operator at the top of the stack and pushes in s2，Discard the pair until you encounter the left parenthesis
                while(!s1.peek().equals("(")) {
                    s2.add(s1.pop());
                }
                s1.pop();//!!! take ( Eject s1 Stack, remove parentheses
            } else {
                //When item Priority is less than or equal to s1 Top Stack Operator, take s1 Operators at the top of the stack pop up and join s2 Medium, go to again(4.1)and s1 New stack top operator comparison in
                //Problem: We lack a way to compare priorities
                while(s1.size() != 0 && Operation.getValue(s1.peek()) >= Operation.getValue(item) ) {
                    s2.add(s1.pop());
                }
                //You will also need to item Push on Stack
                s1.push(item);
            }
        }
        
        //take s1 The remaining operators in the pop-up and join in turn s2
        while(s1.size() != 0) {
            s2.add(s1.pop());
        }

        return s2; //Note because it is stored in List, So the sequential output corresponds to the corresponding suffix expression List
        
    }
    
    //Method: Convert the infix expression to the corresponding List
    //  s="1+((2+3)×4)-5";
    public static List<String> toInfixExpressionList(String s) {
        //Define a List,Stores the contents of the infix expression
        List<String> ls = new ArrayList<String>();
        int i = 0; //This is a pointer that traverses the infix expression string
        String str; // Stitching of multiple digits
        char c; // Every character traversed, it is placed in the c
        do {
            //If c Is a non-number, I need to join ls
            if((c=s.charAt(i)) < 48 ||  (c=s.charAt(i)) > 57) {
                ls.add("" + c);
                i++; //i Need to move back
            } else { //If it is a number, consider multiple digits
                str = ""; //First put str Set up"" '0'[48]->'9'[57]
                while(i < s.length() && (c=s.charAt(i)) >= 48 && (c=s.charAt(i)) <= 57) {
                    str += c;//Stitching
                    i++;
                }
                ls.add(str);
            }
        }while(i < s.length());
        return ls;//Return
    }
    
    //Put an inverse Polish expression, data and operators in turn ArrayList in
    public static List<String> getListString(String suffixExpression) {
        //take suffixExpression Division
        String[] split = suffixExpression.split(" ");
        List<String> list = new ArrayList<String>();
        for(String ele: split) {
            list.add(ele);
        }
        return list;
        
    }
    
    //Complete the operation of the inverse Polish expression
    /*
     * 1)Scan from left to right to push 3 and 4 onto the stack;
        2)Encountered the + operator, so pop up 4 and 3 (4 is the top element, 3 is the second top element), calculate the value of 3+4, get 7, and put 7 on the stack;
        3)Put 5 on the stack;
        4)Next is the * operator, so pop up 5 and 7, calculate 7 * 5 = 35, put 35 on the stack;
        5)Put 6 on the stack;
        6)The final result is the -operator, which calculates the value of 35-6, or 29.
     */

    public static int calculate(List<String> ls) {
        // Create to Stack, Just one stack is needed
        Stack<String> stack = new Stack<String>();
        // ergodic ls
        for (String item : ls) {
            // Use regular expressions to take out numbers here
            if (item.matches("\\d+")) { // Multiple digits matched
                // Push
                stack.push(item);
            } else {
                // pop Out two numbers, combine them, and put them on the stack
                int num2 = Integer.parseInt(stack.pop());
                int num1 = Integer.parseInt(stack.pop());
                int res = 0;
                if (item.equals("+")) {
                    res = num1 + num2;
                } else if (item.equals("-")) {
                    res = num1 - num2;
                } else if (item.equals("*")) {
                    res = num1 * num2;
                } else if (item.equals("/")) {
                    res = num1 / num2;
                } else {
                    throw new RuntimeException("Error in operator");
                }
                //hold res Push
                stack.push("" + res);
            }
            
        }
        //Last stayed stack The data in is the result of the operation
        return Integer.parseInt(stack.pop());
    }
}

//Write a class Operation You can return the priority corresponding to an operator
class Operation {
    private static int ADD = 1;
    private static int SUB = 1;
    private static int MUL = 2;
    private static int DIV = 2;
    
    //Write a method that returns the corresponding priority number
    public static int getValue(String operation) {
        int result = 0;
        switch (operation) {
        case "+":
            result = ADD;
            break;
        case "-":
            result = SUB;
            break;
        case "*":
            result = MUL;
            break;
        case "/":
            result = DIV;
            break;
        default:
            System.out.println("The operator does not exist" + operation);
            break;
        }
        return result;
    }
}