Stack

Introduction of stack

(1) Introduction of stack

(2) Introduction to stack

1. Stack (stack)
2. A stack is an ordered list of Filo first in last out.
3. Stack is a special linear table that restricts the insertion and deletion of elements in a linear table to the same end of the linear table. The end that allows insertion and deletion is the changing end, which is called the top of the stack, and the other end is the fixed end, which is called the bottom of the stack.
4. According to the definition of stack, the first element put in the stack is at the bottom of the stack, the last element put in is at the top of the stack, while the deleted element is just the opposite. The last element put in is deleted first, and the first element is deleted last

(3) pop and push

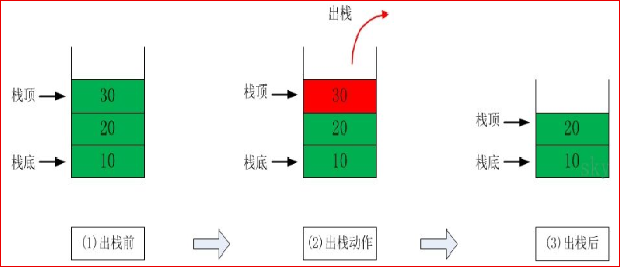
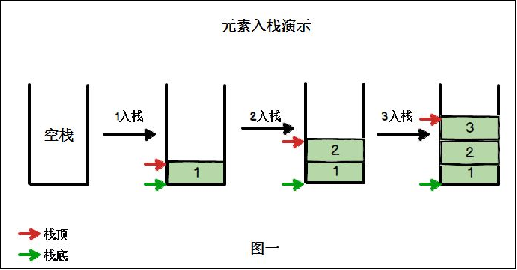
(4) Application scenario of stack

1. Subroutine call: before jumping to the subroutine, the address of the next instruction will be stored in the stack until the subroutine is executed, and then the address will be taken out to return to the original program.
2. Handling recursive calls: similar to subroutine calls, except that in addition to storing the address of the next instruction, parameters, area variables and other data are also stored in the stack.
3. Expression conversion [infix expression to suffix expression] and evaluation (actual solution).
4. Traversal of binary tree.
5. The depth first search method of graphics.

Implementation of stack

(1) Thought analysis of realizing stack

1. Use arrays to simulate stacks
2. Define a top to represent the top of the stack and initialize it to - 1
3. When data is added to the stack, top++; stack[top] = data;
4. Stack out operation, int value = stack[top]; top--, return value
   
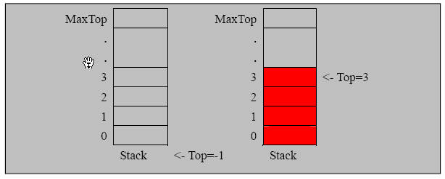
   (2) Code implementation

//Define a class to represent the stack structure
class ArrayStack{
	private int maxSize;//Stack size
	private int[] stack;//Array, array simulation stack, array is placed in the array
	private int top = -1;//Stack top
	
	//constructor 
	public ArrayStack(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[this.maxSize];
	}
	
	//Stack full
	public boolean isFull() {
		return top == maxSize-1;
	}
	
	//Stack empty
	public boolean isEmpty() {
		return top == -1;
	}
	
	//Push 
	public void push(int value) {
		//Determine whether the stack is full
		if(isFull()) {
			System.out.println("Stack full");
			return;
		}
		top++;
		stack[top]=value;
	}
	
	//Out of stack
	public int pop() {
		//First judge whether the stack is empty
		if(isEmpty()) {
			//Throw exception
			throw new RuntimeException("Stack empty, no data//");
		}
		int value = stack[top];
		top--;
		return value;
	}
	
	//Display the stack [traverse the stack]. When traversing, you need to display data from the top of the stack
	public void list() {
		//First judge whether the stack is empty
		if(isEmpty()) {
			//Throw exception
			throw new RuntimeException("Stack empty, no data//");
		}
		for(int i = top;i>=0;i--) {
			System.out.printf("stack[%d]=%d \n",i,stack[i]);
		}
	}
	
}

Use the stack to complete the evaluation of an expression (infix expression)

(1) Train of thought analysis

1. Through an index value (index), we iterate through our expression
2. If we find that it is a number, we will directly enter the number stack
3. If it is found that a symbol is scanned, it can be divided into the following situations
   3.1 if the current symbol stack is found to be empty, it will be directly put into the stack
   3.2 if there are operators in the symbol stack, compare them. If the priority of the current operator is less than or equal to that of the operators in the stack, you need to pop two numbers from the number stack, pop a symbol from the symbol stack, and carry out the operation. The result will be put into the number stack, and then put the current operator into the symbol stack, If the priority of the current operator is higher than that of the operator on the stack, it is directly put into the symbol stack
4. When the expression is scanned, pop out the corresponding numbers and symbols from the number stack and symbol stack in sequence and run
5. Finally, there is only one number on the number stack, which is the result of the expression

(2) Code implementation

package NO03;


public class Calculator {

	public static void main(String[] args) {
		//Complete the operation of the expression according to the idea
		String expression = "70+2*6-4";
		//Create two stacks, number stack and symbol stack
		ArrayStack2 numStack = new ArrayStack2(10);
		ArrayStack2 operStack = new ArrayStack2(10);
		//Define the required related variables
		int index = 0;//For scanning
		int num1 = 0;
		int num2 = 0;
		int oper = 0;
		int res = 0;
		char ch = ' ';//Save the char obtained from each scan to ch
		String keepNum = "";//Multi bit number for splicing
		//Start scan expression for while loop
		while (true) {
			//Get each character of expression in turn
			ch = expression.substring(index, index+1).charAt(0);
			//Judge what ch is, and then deal with it accordingly
			if(operStack.isOper(ch)) {//If operator
				//Judge whether the current symbol stack is empty
				if(!operStack.isEmpty()) {
					//handle
					//If the priority of the current operator is less than or equal to the operator in the stack, you need to pop out two numbers from the number stack,
					//pop out a symbol from the symbol stack, perform the operation, get the result, put it into the number stack, and then put the current operator into the symbol stack
					if(operStack.priority(ch)<=operStack.priority(operStack.peek())) {
						num1 = numStack.pop();
						num2 = numStack.pop();
						oper = operStack.pop();
						res = numStack.cal(num1, num2, oper);
						//Put the result of the operator on the stack
						numStack.push(res);
						//Then put the current operator on the symbol stack
						operStack.push(ch);
					}else {//If the priority of the current operator is higher than that of the operator on the stack, it is directly put into the symbol stack
						operStack.push(ch);
					}
				}else {
					//If empty, direct access symbol stack
					operStack.push(ch);
				}
			}else {//If we find that it is a number, we will directly enter the number stack
//				numStack.push(ch-48);// The difference between character 1 and digit 1 in ascall code table is 48
				//When processing a multi digit number, it cannot be found that it is a single digit and immediately put on the stack, because it may be a multi digit number
				//When processing numbers, you need to look at one bit after the index of the expression. If it is a number, it will be scanned. If it is a symbol, it will be put on the stack
				//Therefore, we need to define a variable string for splicing
				
				//Number of processing bits
				keepNum+=ch;
				
				//If ch is already the last bit of expression, it is directly put on the stack
				if(index==expression.length()-1) {
					numStack.push(Integer.parseInt(keepNum));
				}else {
					//Judge whether the next character is a number. If it is a number, it will continue to scan. If it is an operator, it will be put on the stack
					if(operStack.isOper(expression.substring(index+1, index+2).charAt(0))) {
						//If the last bit is an operator, it is stacked
						numStack.push(Integer.parseInt(keepNum));
						//important!!!!!. keepNum empty
						keepNum = "";
					}
				}
				
			}
			//Let index+1 and judge whether to scan to the end of expression
			index++;
			if(index>=expression.length()) {
				break;
			}
		}
		//When the expression is scanned, pop out the corresponding numbers and symbols from the number stack and symbol stack in sequence and run
		while (true) {
			//If the symbol stack is empty, the final result will be calculated, and there is only one number [result] in the number stack
			if(operStack.isEmpty()) {
				break;
			}
			num1 = numStack.pop();
			num2 = numStack.pop();
			oper = operStack.pop();
			res = numStack.cal(num1, num2, oper);
			numStack.push(res);//Push 
		}
		//pop out the last number of the stack and calculate the result
		System.out.printf("expression%s = %d",expression,numStack.pop());
	}

}


//Create a stack
//Define a class to represent the stack structure, and the function needs to be extended
class ArrayStack2{
	private int maxSize;//Stack size
	private int[] stack;//Array, array simulation stack, array is placed in the array
	private int top = -1;//Stack top
	
	//constructor 
	public ArrayStack2(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[this.maxSize];
	}
	
	//Stack full
	public boolean isFull() {
		return top == maxSize-1;
	}
	
	//Stack empty
	public boolean isEmpty() {
		return top == -1;
	}
	
	//Push 
	public void push(int value) {
		//Determine whether the stack is full
		if(isFull()) {
			System.out.println("Stack full");
			return;
		}
		top++;
		stack[top]=value;
	}
	
	//Out of stack
	public int pop() {
		//First judge whether the stack is empty
		if(isEmpty()) {
			//Throw exception
			throw new RuntimeException("Stack empty, no data//");
		}
		int value = stack[top];
		top--;
		return value;
	}
	
	//Display the stack [traverse the stack]. When traversing, you need to display data from the top of the stack
	public void list() {
		//First judge whether the stack is empty
		if(isEmpty()) {
			//Throw exception
			System.out.println("Stack empty, no data");
		}
		for(int i = top;i>=0;i--) {
			System.out.printf("stack[%d]=%d \n",i,stack[i]);
		}
	}
	
	//Returns the priority of the operator. The priority is determined by the programmer. The priority is expressed in numbers
	//The higher the number, the higher the priority
	public int priority(int oper) {
		if(oper == '*'||oper == '/') {
			return 1;
		}else if (oper == '+'||oper == '-') {
			return 0;
		}else {
			return -1;//Assume that there are only +, -, *, in the current expression/
		}
	}
	
	//Determine whether it is an operator
	public boolean isOper(char val) {
		return val=='+'||val=='-'||val=='*'||val=='/';
	}
	
	//computing method
	public int cal(int num1,int num2,int oper) {
		int res=0;//Used to store calculation results
		switch (oper) {
		case '+':
			res = num1+num2;
			break;
		case '-':
			res = num2-num1;//Pay attention to the order
			break;
		case '*':
			res = num1*num2;
			break;
		case '/':
			res = num2/num1;
			break;

		default:
			break;
		}
		return res;
	}
	
	//Add a method to return the value at the top of the current stack, but it is not a real pop
	public int peek() {
		return stack[top];
	}
}

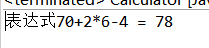
Note: the implementation of single digit operation is extended to multi digit operation

Prefix expression (Polish expression)

(1) Introduction:

1. Prefix expression is also called polish. The operator of prefix expression precedes the operand
2. Example: (3 + 4) × The prefix expression corresponding to 5-6 is- × + 3 4 5 6

(2) Computer evaluation of prefix expressions

Scan the expression from right to left. When encountering a number, push the number into the stack. When encountering an operator, pop up the two numbers at the top of the stack, use the operator to calculate them (top element and secondary top element), and put the result into the stack; Repeat the above process until the leftmost end of the expression. The value obtained by the final operation is the result of the expression

Suffix expression (inverse Polish expression)

(1) Introduction

1. Suffix expressions, also known as inverse Polish expressions, are similar to prefix expressions, except that the operator is after the operand
2. Example: (3 + 4) × The suffix expression corresponding to 5-6 is 3, 4 + 5 × 6 –
   

(2) Computer evaluation of suffix expressions

Scan the expression from left to right. When encountering a number, push the number into the stack. When encountering an operator, pop up the two numbers at the top of the stack, use the operator to calculate them (secondary top element and top element), and put the result into the stack; Repeat the above process until the rightmost end of the expression. The value obtained by the final operation is the result of the expression

(3) Complete an inverse Polish calculator

Task point:

1. Enter an inverse Polish expression (suffix expression), use stack, and calculate the result
2. It supports parentheses and multi digit integers, because here we mainly talk about data structures, so the calculator is simplified and only supports the calculation of integers.
3. Train of thought analysis
4. Code complete

Code implementation:

package NO03;

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

public class PolandNotation {

	public static void main(String[] args) {
		// First define an inverse Polish expression
		//(3+4) × The suffix expression corresponding to 5-6 is 3, 4 + 5 ×  6 -
		//For convenience, the numbers and symbols of the inverse Polish expression are separated by spaces
		String suffixExpression = "30 4 + 5 * 6 -";
		//Idea:
		//1. First "3 4 + 5" ×  6 - "put in ArrayList
		//2. Pass the ArrayList to a method and traverse the matching stack to complete the calculation
		List<String> list = getListString(suffixExpression);
		System.out.println("List="+list);
		
		int res = calculate(list);
		System.err.println("The result of the calculation is:"+res);

	}
	
	
	//Put an inverse expression, and then put the data and operators into the ArrayList
	public static List<String> getListString(String suffixExpression){
		//Split suffixExpression
		String[] split = suffixExpression.split(" ");
		List<String> list = new ArrayList<String>();
		for(String ele:split) {
			list.add(ele);
		}
		return list;
	}
	
	//Complete the operation of the inverse Polish expression
	/**
	 * 
		1. Scan from left to right and press 3 and 4 into the stack;
		2. Encounter the + operator, so pop up 4 and 3 (4 is the top element of the stack and 3 is the secondary top element), calculate the value of 3 + 4, get 7, and then put 7 on the stack;
		3. Stack 5;
		4. Next is × Operator, so pop up 5 and 7 and calculate 7 × 5 = 35, put 35 into the stack;
		5. Stack 6;
		6. Finally, the - Operator calculates the value of 35-6, i.e. 29, to get the final result
	 * 
	 */
	public static int calculate(List<String> ls) {
		//To create a stack, you only need one
		Stack<String> stack = new Stack<String>();
		//Traversal ls
		for(String item: ls ) {
			if(item.matches("\\d+")) {
				//Push 
				stack.push(item);
			}else {
				//pop out two numbers, and operation, in the stack
				int num2 = Integer.parseInt(stack.pop());
				int num1 = Integer.parseInt(stack.pop());
				int res = 0;
				if(item.equals("+")) {
					res = num1+num2;
				}else if(item.equals("-")) {
					res = num1-num2;
				}else if(item.equals("*")) {
					res = num1*num2;
				}else if(item.equals("/")) {
					res = num1/num2;
				}else {
					throw new RuntimeException("Incorrect operator");
				}
				//Put res on the stack
				stack.push(""+res);
			}
		}//The last data left in the stack is the operation result
		return Integer.parseInt(stack.pop());
	}

}