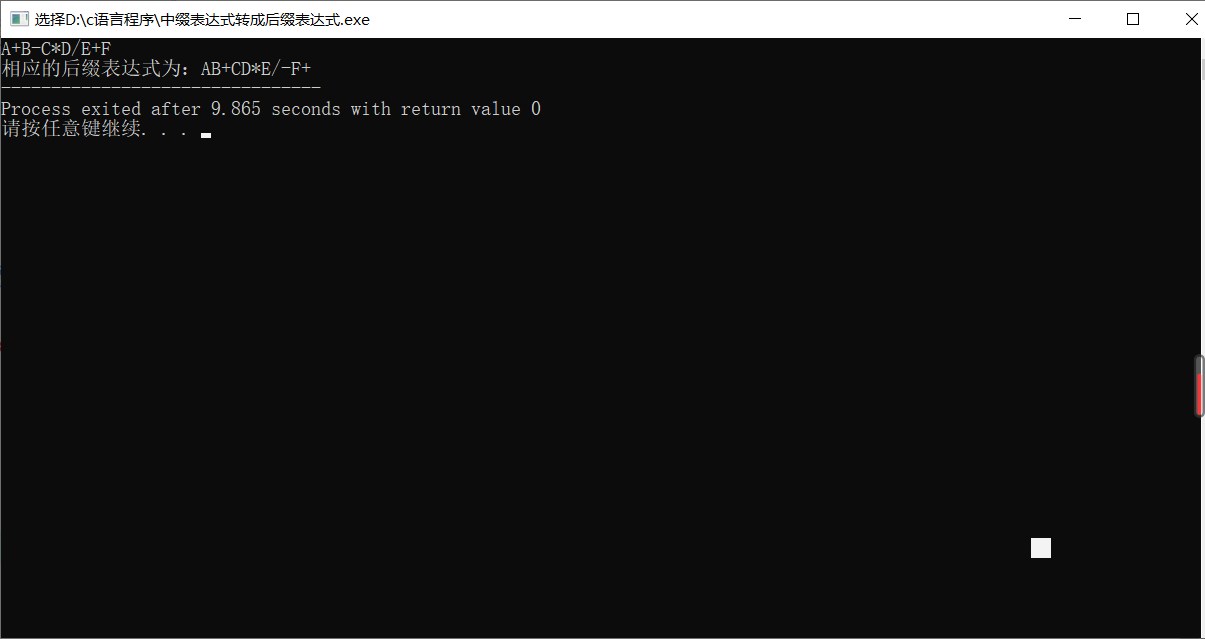
• Infix expression: the operator is between two operands
• Prefix expression: the operator precedes the two operands (the left-right order of the two operands cannot be reversed)
• Suffix expression: operator after two operands
  

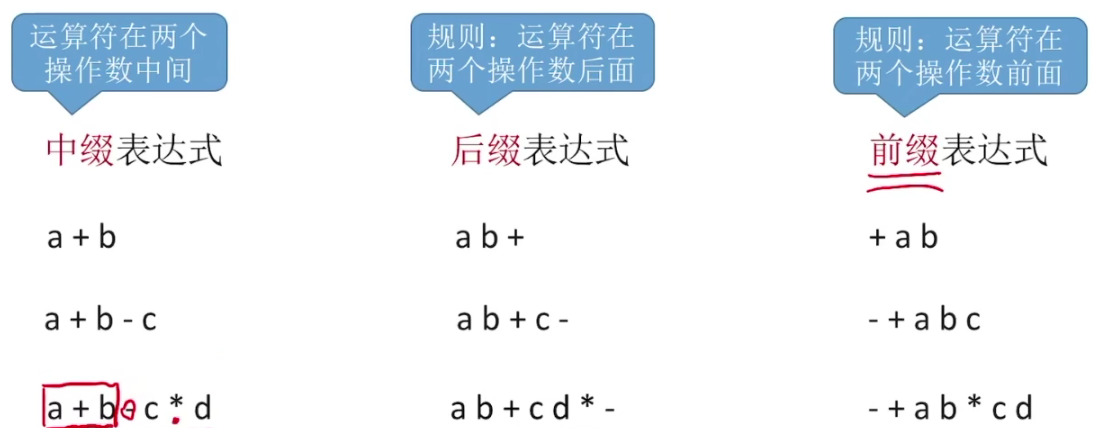
Manual calculation method of infix expression to suffix expression:

Objectively speaking, the two calculation results are correct, but the computer algorithm calculation result is the former, so the result obtained according to the "left first" principle can be the same as that calculated by the computer algorithm. It is recommended to use the left calculation method, that is, according to the left first principle.
The left to right order of the evaluators in the suffix expression calculated by the left priority principle is the same as that in the infix expression according to the left priority principle.

Calculation of suffix expression:

Manual calculation:

Note the left-right order of the two operands.

Computer calculation:

Because each calculation of the post order expression allows the two most recent operands in front of the operator to perform the corresponding calculation, which is consistent with the last in first out principle of the stack, the data mechanism stack is used to calculate the suffix expression.

Manual calculation method of infix expression to prefix expression:
The calculation result on the right is the result calculated according to the right priority principle. The reason and effect of using the right priority principle are the same as that of the left priority principle. Only the operators in the prefix expression calculated according to the right first principle are in the same order from right to left as the operators in the infix expression.

Calculation of prefix expression:

Note: prefix expressions are evaluated from right to left, and suffix expressions are evaluated from left to right.
The principle of manual calculation is the same as that of prefix expression.

Code implementation of infix expression to suffix expression:

Suffix expression is also called inverse Polish expression. Suffix expression is widely used in computer field. The algorithm of converting infix expression into suffix expression is very important.

Algorithm idea:

Initializes a stack to store operators whose operation order cannot be determined temporarily.
Processing each element of infix expression from left to right until the end may encounter three situations:

1. An operand (such as a number) is encountered; Add suffix expression directly.
2. Encounter delimiter (parenthesis); In case of '(' directly put on the stack; in case of ')', pop up the operators in the stack and add the suffix expression until '(' pops up. Note: '(' does not add the suffix expression.
3. When encountering operators (addition, subtraction, multiplication and division), pop up all operators with priority higher than or equal to the current operator in the stack in turn, and add suffix expression. If it encounters' ('or the stack is empty, stop. Then put the current operator into the stack.
After all elements are processed according to the above method, the remaining operators in the stack will pop up in turn and be added to the suffix expression.

#include<iostream>
#include<unordered_map>
using namespace std;
//Infix expression to suffix expression 

unordered_map<char,int>mp; //Define hash table record operator level 

struct Stack{
	char data;
	Stack *next;
};

//Initialization stack
void InitStack(Stack * &S){
	
	S=(Stack *)malloc(sizeof(Stack));
	S->next=NULL;
	
} 

//Determine whether the stack is empty
bool IsEmpty(Stack * &S){
	
	return S->next==NULL;
	
} 

//Push 
void StackPush(Stack * &S,char value){
	
	Stack *p=(Stack *)malloc(sizeof(Stack));
	p->data=value;
	p->next=S->next;
	S->next=p;
	
} 

//Out of stack
void StackPop(Stack * &S){
	
	if(IsEmpty(S))
		return;
	
	Stack *p=S->next;
	S->next=p->next;
	free(p); 
	
} 

//Get stack top element
char StackGetTop(Stack * &S){
	
	if(IsEmpty(S))
		return '!';
		
	return S->next->data;	
} 

//Convert prefix expression to suffix expression
void Transform(Stack * &S,string &Qstr,string &Hstr){
	
	for(int i=0;i<Qstr.length();i++){
		
		if(Qstr[i]>='a'&&Qstr[i]<='z'||Qstr[i]>='A'&&Qstr[i]<='Z'){
			Hstr+=Qstr[i];
		}else if(Qstr[i]=='('){
			StackPush(S,'C');
		}else if(Qstr[i]==')'){		
			while(StackGetTop(S)!='('){
				Hstr+=StackGetTop(S);
				StackPop(S);
			}
			StackPop(S);
		}else{
			char c=Qstr[i];
			while(!IsEmpty(S)){
				
				char t=StackGetTop(S);
				if(t=='('){
					break;
				}
					
				if(mp[t]>=mp[c]){
					Hstr+=t;
					StackPop(S);
				}else{
					break;
				}
			}
			StackPush(S,c);
		}
		
	}
	while(!IsEmpty(S)){
		Hstr+=StackGetTop(S);
		StackPop(S);
	}
} 
 

int main(){
	
	Stack *S; //Define a stack
	string Zstr,Hstr=""; //Define prefix expression suffix expression 
	mp['+']=1; mp['-']=1; mp['*']=2; mp['/']=2; //Record operator level 
	
	getline(cin,Zstr); //Enter prefix expression 
	
	InitStack(S); //Initialization stack 
	
	Transform(S,Zstr,Hstr); //Convert prefix expression to suffix expression 
	
	cout<<Hstr; //Output suffix expression 
	
	return 0;
} 

/**
A+B-C*D/E+F 
AB+CD*E/-F+
*/