catalogue

• preface

• Spring Boot version

• What is a filter?

• Implementation principle of Filter

• How to customize a Filter?

• How does Spring Boot configure a Filter?

  • Use @ Bean injection in the configuration class [recommended]

  • Use @ WebFilter

• Take a chestnut

• summary

preface

The previous article introduced how to configure interceptors in Spring Boot. Today's article will talk about a component similar to interceptors: filters.

In fact, in the actual development, the filter really has little contact, but it plays an indispensable role in the application. It is worth spending a chapter on it.

Spring Boot version

The version of Spring Boot based on this article is 2.3.4.RELEASE.

What is a filter?

Filter is also called filter. It is the most practical technology in Servlet Technology. Web developers use filter technology to intercept all web resources managed by web server, such as JSP, servlet, static picture file or static HTML file, so as to realize some special functions. For example, it implements some advanced functions such as URL level permission control, filtering sensitive words, compressing response information and so on.

Implementation principle of Filter

When the client sends a request for a Web resource, the Web server checks according to the filtering rules set in the application configuration file. If the client request meets the filtering rules, it intercepts the client request / response, checks or changes the request header and request data, passes through the filter chain in turn, and finally hands the request / response to the requested Web resource for processing. The request information can be modified in the filter chain, or the request can not be sent to the resource processor according to conditions, and a response can be sent back directly to the client. When the resource processor completes the processing of resources, the response information will be returned in reverse level by level. Similarly, in this process, the user can modify the response information to complete certain tasks, as shown in the following figure:

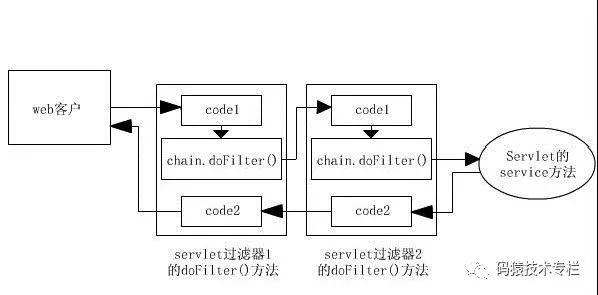
The server will assemble into a chain according to the sequence of Filter definitions, and then execute the doFilter() method one at a time. (Note: This is different between Filter and Servlet) the execution sequence is as shown in the figure below. Execute the code before chain.doFilter() of the first Filter, the code before chain.doFilter() of the second Filter, the requested resources, the code after chain.doFilter() of the second Filter, and the code after chain.doFilter() of the first Filter, Finally, the response is returned.

How to customize a Filter?

In fact, this problem should not be introduced in the Spring Boot chapter. It should be covered in Spring MVC. You only need to implement the javax.servlet.Filter interface and rewrite the methods therein. Examples are as follows:

@Component
public class CrosFilter implements Filter {

    //Override the doFilter method
    @Override
    public void doFilter(ServletRequest req, ServletResponse res, FilterChain chain) throws IOException, ServletException {
        //Proceed to the next filter
        chain.doFilter(req, response);
    }

How does Spring Boot configure a Filter?

After customizing the Filter, of course, you need to make it effective in Spring Boot. There are two ways to configure the Filter in Spring Boot. In fact, they are very simple, which are introduced one by one below.

Use @ Bean injection in the configuration class [recommended]

In fact, it is very simple. You only need to inject the instance of FilterRegistrationBean into the IOC container, as follows:

@Configuration
public class FilterConfig {
    @Autowired
    private Filter1 filter1;

    @Autowired
    private Filter2 filter2;


    /**
     * Inject Filter1
     * @return
     */
    @Bean
    public FilterRegistrationBean filter1() {
        FilterRegistrationBean registration = new FilterRegistrationBean();
        registration.setFilter(filter1);
        registration.addUrlPatterns("/*");
        registration.setName("filter1");
        //Set priority
        registration.setOrder(1);
        return registration;
    }

    /**
     * Injection Filter2
     * @return
     */
    @Bean
    public FilterRegistrationBean filter2() {
        FilterRegistrationBean registration = new FilterRegistrationBean();
        registration.setFilter(filter2);
        registration.addUrlPatterns("/*");
        registration.setName("filter2");
        //Set priority
        registration.setOrder(2);
        return registration;
    }
}

Note: the priority level set determines the execution order of the filter.

Use @ WebFilter

@WebFilter is an annotation of servlet 3.0, which is used to label a Filter. Spring Boot also supports this method. You only need to label the annotation on the custom Filter, as follows:

@WebFilter(filterName = "crosFilter",urlPatterns = {"/*"})
public class CrosFilter implements Filter {

    //Override the doFilter method
    @Override
    public void doFilter(ServletRequest req, ServletResponse res, FilterChain chain) throws IOException, ServletException {
        //Proceed to the next filter
        chain.doFilter(req, response);
    }
}

To make the @ WebFilter annotation effective, you need to mark another annotation @ ServletComponentScan on the configuration class for scanning to make it effective, as follows:

@SpringBootApplication
@ServletComponentScan(value = {"com.example.springbootintercept.filter"})
public class SpringbootApplication {}

At this point, the configuration is completed. Start the project and it can run normally.

Take a chestnut

Cross domain is a difficult problem for projects with front-end and back-end separation. What is cross domain? How? This is not the focus of this chapter.

There are many solutions to cross domain problems, such as JSONP, gateway support, etc. About cross domain problems and how Spring Boot gracefully solves cross domain problems? It will be introduced in subsequent articles. Today we will focus on how to use filters to solve cross domain problems.

In fact, the principle is very simple. You only need to add the corresponding cross domain content in the request header. The following code is just a simple demonstration. You need to improve the detailed content, such as the white list.

@Component
public class CrosFilter implements Filter {

    //Override the doFilter method
    @Override
    public void doFilter(ServletRequest req, ServletResponse res, FilterChain chain) throws IOException, ServletException {
        HttpServletResponse response = (HttpServletResponse) res;
        response.setHeader("Access-Control-Allow-Origin", "*");
        response.setHeader("Access-Control-Allow-Credentials", "true");
        response.setHeader("Access-Control-Allow-Methods", "POST, GET, OPTIONS, DELETE");
        response.setHeader("Access-Control-Max-Age", "3600");
        response.setHeader("Access-Control-Allow-Headers"," Origin, X-Requested-With, Content-Type, Accept");
        //Proceed to the next filter
        chain.doFilter(req, response);
    }
}

Inject FilterRegistrationBean into the configuration class, as shown in the following code:

@Configuration
public class FilterConfig {
    @Autowired
    private CrosFilter crosFilter;

    /**
     * Inject crossfilter
     * @return
     */
    @Bean
    public FilterRegistrationBean crosFilter() {
        FilterRegistrationBean registration = new FilterRegistrationBean();
        registration.setFilter(crosFilter);
        registration.addUrlPatterns("/*");
        registration.setName("crosFilter");
        //Set priority
        registration.setOrder(Ordered.HIGHEST_PRECEDENCE);
        return registration;
    }
}

So far, the configuration is completed, and the relevant detailed functions need to be polished by yourself.

summary

The content of the filter is relatively simple, but it is indispensable in actual development. For example, the commonly used permission control frameworks Shiro and Spring Security use filters internally. Understanding it will play a fundamental role in further learning in the future.