SPOJ 375
meaning of the title
Give you the weight of each edge of a tree. There are two operations: modifying the weight of one edge; asking for the path sum between two points. (Multiple sets of data)
sample input
1
3
1 2 1
2 3 2
QUERY 1 2
CHANGE 1 3
QUERY 1 2
DONE
sample output
1
3
Detailed tree chain dissection
Chain partitioning is a method of converting tree queries into chain queries, that is to say, as long as a single chain can do tree queries, and only add a small constant. So in general, if the part is a single chain, the latter point can certainly be cut into trees.
Subdivision
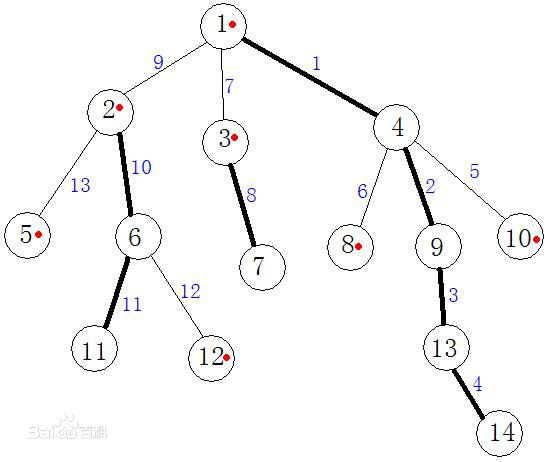
In pretreatment, a tree is divided into several chains, and then maintained in a single chain manner. We call the edges on the chain heavy edges, and the edges between heavy edges and heavy edges light edges. The rough edge in the figure below is the heavy edge. However, it is too complicated to maintain each chain separately, so we can maintain all the links together directly.
There is a property: if the number of dfs of each chain is consecutive according to the double edge dfs (such as accessing 4 after 1 in the figure below). When inquiring, each inquiry is divided into several chains and queried in data structure.
Heuristic partitioning
There are also good and bad divisions. Think about it sensibly (as proved later), because it emphasizes data structure maintenance, complexity is logn, light direct access, complexity is n, then we want to visit as many important sides as possible, here we use a heuristic partition.
Definition:
Depth of dep[x] x node
Subtree size of siz[x] x
Parent node of fa[x] x
id[x] x node number (converted to tree chain number)
son[x] x's second son
The top[x] x is at the top of the heavy chain
Definition of Heavy Son: The Largest siz of All Sons
First, dfs finds out the heavy sons of all nodes, and can process dep, siz, fa at the same time; then dfs searches the heavy sons first, so that a heavy chain can be pulled down, while tracing back, other non-heavy sons continue to pull down a heavy chain in turn. For example, in the figure above, 1, 4, 9, 13, 14 are pulled out at the beginning, then back to 1, visit 2, and then 2 pulls down a heavy chain.
void dfs1(int x,int ftr,int d)
{
dep[x] = d; siz[x] = 1; son[x] = 0; fa[x] = ftr;
for (int i = 0;i < v[x].size(); i++)
{
int nxt = v[x][i];
if (nxt == ftr) continue;
dfs1(nxt,x,d+1);
siz[x] += siz[nxt];
if (siz[nxt] > siz[son[x]]) son[x] = nxt;
}
}
void dfs2(int x,int tp)
{
top[x] = tp; id[x] = ++num;
if (son[x] > 0) dfs2(son[x],tp);
for (int i = 0;i < v[x].size(); i++)
{
int nxt = v[x][i];
if (nxt == fa[x] || nxt == son[x]) continue;
dfs2(nxt,nxt);
}
}The properties of such subdivision are as follows:
1. In light edge (u,v), size (v)<=size (u/2). Apparently by way of counter-evidence.
2. On the path from the root to a certain point, no more than one light edge of logn and no more than one heavy path of logn. Although I won't certify this, I know it guarantees "more visits at a time".
Maintain
Here I use segment tree maintenance. After the previous partitioning, the problem is completely transformed into how to do a single chain, which is very simple.
query
Let's talk about how to query (u,v).
Consider in two cases:
1. u and V are on the same heavy chain, i.e. top[u] = top[v]. It's better to find them directly in the online segment tree, because the nodes from u to V are continuous.
2. u and v are not on the same heavy chain. Compare the starting point of the two chains, which is lower, which node will run to the top of the chain, and then climb up one side (light side) to a new heavy chain, and then cycle. Obviously, this point to the vertex is also continuous, and the time complexity of climbing up a layer of light edge is only o(1).
int link(int u,int v)
{
int top1 = top[u]; int top2 = top[v];
int res = 0;
while (top1 != top2)
{
if (dep[top1] < dep[top2])
{swap(top1,top2); swap(u,v);}
res = max(query(1,id[top1],id[u]),res);
u = fa[top1];
top1 = top[u];
}
if (u == v) return res;
if (dep[u] > dep[v]) swap(u,v);
res = max(query(1,id[son[u]],id[v]),res);
return res;
}Complete code
The encapsulation of tree dissection is better... Most of the time, you just need to study the single chain first, then drag a tree cut, and change the query operation in the link function.
#include<cmath>
#include<cstdio>
#include<vector>
#include<cstring>
#include<iomanip>
#include<stdlib.h>
#include<iostream>
#include<algorithm>
#define ll long long
#define inf 1000000000
#define mod 1000000007
#define N 10005
using namespace std;
struct tree1
{
int x,y,val;
void read(){scanf("%d%d%d",&x,&y,&val);}
} e[N];
vector<int> v[N];
struct tree2
{
int l,r,val;
} tree[N*4];
int dep[N],siz[N],fa[N],id[N],son[N],val[N],top[N];
int T,num,i,n,x,y;
void dfs1(int x,int ftr,int d)
{
dep[x] = d; siz[x] = 1; son[x] = 0; fa[x] = ftr;
for (int i = 0;i < v[x].size(); i++)
{
int nxt = v[x][i];
if (nxt == ftr) continue;
dfs1(nxt,x,d+1);
siz[x] += siz[nxt];
if (siz[nxt] > siz[son[x]]) son[x] = nxt;
}
}
void dfs2(int x,int tp)
{
top[x] = tp; id[x] = ++num;
if (son[x] > 0) dfs2(son[x],tp);
for (int i = 0;i < v[x].size(); i++)
{
int nxt = v[x][i];
if (nxt == fa[x] || nxt == son[x]) continue;
dfs2(nxt,nxt);
}
}
void build(int l,int r,int rt)
{
tree[rt].l = l; tree[rt].r = r;
if (l == r) {tree[rt].val = val[l]; return;}
int mid = (l + r) >> 1;
build(l,mid,rt << 1);
build(mid+1,r,rt << 1 | 1);
tree[rt].val = max(tree[rt<<1].val,tree[rt<<1|1].val);
}
void update(int rt,int key,int val)
{
if (tree[rt].l == tree[rt].r)
{tree[rt].val = val; return;}
int mid = (tree[rt].l + tree[rt].r) >> 1;
if (key <= mid) update(rt<<1,key,val);
else update(rt<<1|1,key,val);
tree[rt].val = max(tree[rt<<1].val,tree[rt<<1|1].val);
}
int query(int rt,int l,int r)
{
if (tree[rt].l >= l && tree[rt].r <= r) return tree[rt].val;
int mid = (tree[rt].l + tree[rt].r) >> 1;
int res = 0;
if (l <= mid) res = max(res,query(rt<<1,l,r));
if (r > mid) res = max(res,query(rt<<1|1,l,r));
return res;
}
int link(int u,int v)
{
int top1 = top[u]; int top2 = top[v];
int res = 0;
while (top1 != top2)
{
if (dep[top1] < dep[top2])
{swap(top1,top2); swap(u,v);}
res = max(query(1,id[top1],id[u]),res);
u = fa[top1];
top1 = top[u];
}
if (u == v) return res;
if (dep[u] > dep[v]) swap(u,v);
res = max(query(1,id[son[u]],id[v]),res);
return res;
}
int main()
{
scanf("%d",&T);
while (T--)
{
scanf("%d",&n);
for (i = 1;i < n; i++)
{
e[i].read();
v[e[i].x].push_back(e[i].y);
v[e[i].y].push_back(e[i].x);
}
num = 0; dfs1(1,0,1); dfs2(1,1);
for (i = 1;i <= n; i++)
{
if (dep[e[i].x] < dep[e[i].y]) swap(e[i].x,e[i].y);
val[id[e[i].x]] = e[i].val;//val array is used to record the weight of the edge above each point
}
build(1,n,1);
char s[40]; scanf("%s",&s);
while (s[0] != 'D')
{
scanf("%d%d",&x,&y);
if (s[0] == 'Q') printf("%d\n",link(x,y));
if (s[0] == 'C') update(1,id[e[x].x],y);
scanf("%s",&s);
}
for(int i = 1;i <= n; i++) v[i].clear();
}
return 0;
}