Thesis title: interpreting task specific knowledge from Bert into simple neural networks Paper link: https://arxiv.org/pdf/1903.12136.pdf
abstract
In the literature of natural language processing, neural networks become more and more deep and complex. The first sign of this trend is the deep language representation model, including BERT, ELMo and GPT. The emergence and evolution of these models even led to the belief that the previous generation, the shallow language understanding neural network (such as LSTM) has become obsolete. However, this paper proves that the basic "lightweight" neural network can still be competitive without the change of network architecture, external training data or other input characteristics. The text abstracts the knowledge in the most advanced language representation model BERT into a single-layer BiLSTM and a Siamese correspondence model for sentence pair tasks. In multiple data sets of semantic understanding, natural language reasoning and emotion classification, the knowledge distillation model obtains the same results as ELMo, the amount of parameters is only about 1 / 100 times that of ELMo, and the reasoning time is 15 times faster.
1 Introduction
In the research of natural language processing, neural network models have become the main force, and the model structures emerge one after another, as if there is no end. The initial neural networks such as LSTM in these processes become easy to be ignored. For example, ELMo model achieved sota effect on some tasks in 2018, and then the bidirectional coding representation model Bert and GPT-2 achieved great improvement on more tasks.
However, such a large model has problems in the process of practical implementation:
- Due to the large number of parameters, such as BERT and GPT-2, it is not deployable in resource constrained systems such as mobile devices.
- Due to low reasoning time efficiency, they may not be suitable for real-time systems, and they are basically unqualified for many scenarios of QPS pressure measurement.
- According to Moore's law, we need to re compress the model and re evaluate the performance of the model after a certain time.
To solve the above problems, this paper proposes an efficient transfer learning method based on domain knowledge:
- The author distilled the bet large into the single-layer BiLSTM, reduced the parameters by 100 times and increased the speed by 15 times. Although the effect is much worse than BERT, it can be tied with ELMo.
- At the same time, due to the limited task data, the author expanded the data 10 + times based on the following rules: randomly replace words with [MASK]; Replace words based on POS tags; Take n-gram randomly from the sample as a new sample
2 related work
For the background introduction of model compression, you can see Li rumor's article https://zhuanlan.zhihu.com/p/273378905 , the summary is relatively refined and in place, and will not be repeated here:
Hinton put forward the concept of Knowledge Distillation in NIPS2014[1], which aims to transfer the knowledge learned from a large model or multiple models to another lightweight single model for easy deployment. In short, it is to use the small model to learn the prediction results of the large model, rather than directly learning the label in the training set.
In the process of distillation, we call the original large model teacher model, the new small model student model, the label in the training set hard label, the probability output predicted by the teacher model soft label, and temperature(T) is used to adjust the super parameters of the soft label.
The core idea of distillation is that the goal of a good model is not to fit the training data, but to learn how to generalize to new data. Therefore, the goal of distillation is to let the student model learn the generalization ability of the teacher model, and the results obtained in theory will be better than the student model simply fitting the training data.
After BERT put forward, how to lose weight has become an important branch. The main methods are pruning, distillation and quantification. The quantitative improvement is limited, so it is inevitable to use the fusion method of pruning + distillation to obtain better results. Next, we will introduce the main development context of BERT distillation. According to various studies, the improvement of distillation comes from distillation in fine tuning stage - > pre training stage on the one hand, and from the last layer of knowledge - > hidden layer knowledge - > distillation attention matrix on the other hand.
3 model method
The first step of this paper is to select the teacher model and student model. The second step is to establish the distillation program: establish the logit region objective function and build the migration data set.
3.1 model selection
For the "teacher" model, this paper selects Bert to do fine-tuning tasks, such as text classification, text pair classification, etc. For text classification, you can directly input the text into Bert, get cls and output softmax directly, and you can get the probability of each label:
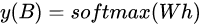
Where W\in R^{k *d}
Is the softmax weight matrix, and k is the number of categories. For the text pair task, we can directly input two texts into Bert to extract features, and then classify them into softmax.
For the "student" model, this paper selects BiLSTM and a nonlinear classifier. As shown in the figure below:


The main process is to represent the text word vector, input it to BiLSTM, select the forward and reverse last-minute hidden layer output and splice it, then output it through a relu and input it to softmax to get the final probability.
3.2 distillation objectives
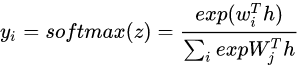
Where w_{i} Is the ith row of the weight matrix W, and z is equal to w^Th
The goal of distillation is to minimize the square error MSE between student model and teacher model:
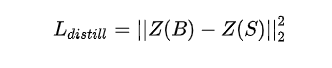
Where Z(B) and Z(S) categories represent the logit output of the teacher and student models
The training function of the final distillation model can combine MSE loss and cross entropy loss:
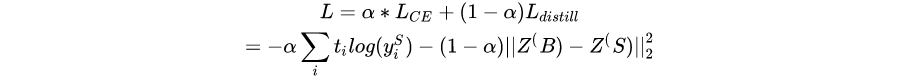
3.3 data enhancement
- Randomly replace the word with [MASK]: "I loved the comedy." becomes "I [MASK] the comedy."
- Replace words based on POS tags; "What do pigs eat?" becomes "How do pigs eat?"
- Take n-gram randomly from the sample as a new sample
4 experimental results
The data sets used in this paper are SST-2, MNLI and QQP The experimental results are as follows:
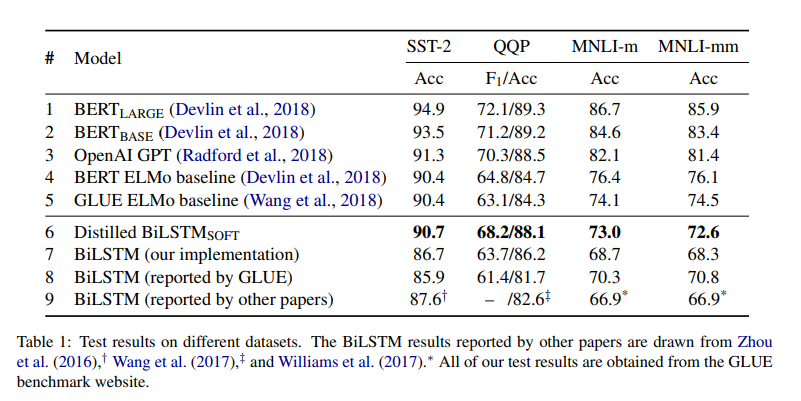
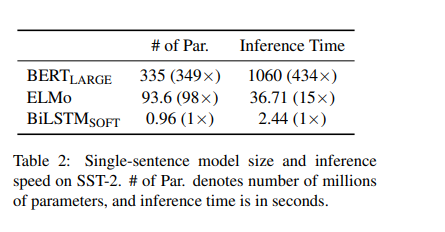
Faster reasoning:
5 distillation code
https://github.com/qiangsiwei/bert_distill
# coding:utf-8
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torch.autograd import Variable
from keras.preprocessing import sequence
import pickle
from tqdm import tqdm
import numpy as np
from transformers import BertTokenizer
from utils import load_data
from bert_finetune import BertClassification
USE_CUDA = torch.cuda.is_available()
if USE_CUDA: torch.cuda.set_device(0)
FTensor = torch.cuda.FloatTensor if USE_CUDA else torch.FloatTensor
LTensor = torch.cuda.LongTensor if USE_CUDA else torch.LongTensor
device = torch.device('cuda' if USE_CUDA else 'cpu')
class RNN(nn.Module):
def __init__(self, x_dim, e_dim, h_dim, o_dim):
super(RNN, self).__init__()
self.h_dim = h_dim
self.dropout = nn.Dropout(0.2)
self.emb = nn.Embedding(x_dim, e_dim, padding_idx=0)
self.lstm = nn.LSTM(e_dim, h_dim, bidirectional=True, batch_first=True)
self.fc = nn.Linear(h_dim * 2, o_dim)
self.softmax = nn.Softmax(dim=1)
self.log_softmax = nn.LogSoftmax(dim=1)
def forward(self, x):
embed = self.dropout(self.emb(x))
out, _ = self.lstm(embed)
hidden = self.fc(out[:, -1, :])
return self.softmax(hidden), self.log_softmax(hidden)
class Teacher(object):
def __init__(self, bert_model='bert-base-chinese', max_seq=128, model_dir=None):
self.max_seq = max_seq
self.tokenizer = BertTokenizer.from_pretrained(bert_model, do_lower_case=True)
self.model = torch.load(model_dir)
self.model.eval()
def predict(self, text):
tokens = self.tokenizer.tokenize(text)[:self.max_seq]
input_ids = self.tokenizer.convert_tokens_to_ids(tokens)
input_mask = [1] * len(input_ids)
padding = [0] * (self.max_seq - len(input_ids))
input_ids = torch.tensor([input_ids + padding], dtype=torch.long).to(device)
input_mask = torch.tensor([input_mask + padding], dtype=torch.long).to(device)
logits = self.model(input_ids, input_mask, None)
return F.softmax(logits, dim=1).detach().cpu().numpy()
def train_student(bert_model_dir="/data0/sina_up/dajun1/src/doc_dssm/sentence_bert/bert_pytorch",
teacher_model_path="./model/teacher.pth",
student_model_path="./model/student.pth",
data_dir="data/hotel",
vocab_path="data/char.json",
max_len=50,
batch_size=64,
lr=0.002,
epochs=10,
alpha=0.5):
teacher = Teacher(bert_model=bert_model_dir, model_dir=teacher_model_path)
teach_on_dev = True
(x_tr, y_tr, t_tr), (x_de, y_de, t_de), vocab_size = load_data(data_dir, vocab_path)
l_tr = list(map(lambda x: min(len(x), max_len), x_tr))
l_de = list(map(lambda x: min(len(x), max_len), x_de))
x_tr = sequence.pad_sequences(x_tr, maxlen=max_len)
x_de = sequence.pad_sequences(x_de, maxlen=max_len)
with torch.no_grad():
t_tr = np.vstack([teacher.predict(text) for text in t_tr])
t_de = np.vstack([teacher.predict(text) for text in t_de])
with open(data_dir+'/t_tr', 'wb') as fout: pickle.dump(t_tr,fout)
with open(data_dir+'/t_de', 'wb') as fout: pickle.dump(t_de,fout)
model = RNN(vocab_size, 256, 256, 2)
if USE_CUDA: model = model.cuda()
opt = optim.Adam(model.parameters(), lr=lr)
ce_loss = nn.NLLLoss()
mse_loss = nn.MSELoss()
for epoch in range(epochs):
losses, accuracy = [], []
model.train()
for i in range(0, len(x_tr), batch_size):
model.zero_grad()
bx = Variable(LTensor(x_tr[i:i + batch_size]))
by = Variable(LTensor(y_tr[i:i + batch_size]))
bl = Variable(LTensor(l_tr[i:i + batch_size]))
bt = Variable(FTensor(t_tr[i:i + batch_size]))
py1, py2 = model(bx)
loss = alpha * ce_loss(py2, by) + (1-alpha) * mse_loss(py1, bt) # in paper, only mse is used
loss.backward()
opt.step()
losses.append(loss.item())
for i in range(0, len(x_de), batch_size):
model.zero_grad()
bx = Variable(LTensor(x_de[i:i + batch_size]))
bl = Variable(LTensor(l_de[i:i + batch_size]))
bt = Variable(FTensor(t_de[i:i + batch_size]))
py1, py2 = model(bx)
loss = mse_loss(py1, bt)
if teach_on_dev:
loss.backward()
opt.step()
losses.append(loss.item())
model.eval()
with torch.no_grad():
for i in range(0, len(x_de), batch_size):
bx = Variable(LTensor(x_de[i:i + batch_size]))
by = Variable(LTensor(y_de[i:i + batch_size]))
bl = Variable(LTensor(l_de[i:i + batch_size]))
_, py = torch.max(model(bx, bl)[1], 1)
accuracy.append((py == by).float().mean().item())
print(np.mean(losses), np.mean(accuracy))
torch.save(model, student_model_path)
if __name__ == "__main__":
train_student()