subject

SP375 QTREE - Query on a tree

analysis

It's also a blue question, because it's longer
Tree cut open questions (basically), single point modification, chain query.

We can see that in this problem, we operate on the edge, and our tree section operates on the nodes, so we consider to transfer the edge weight to the point weight.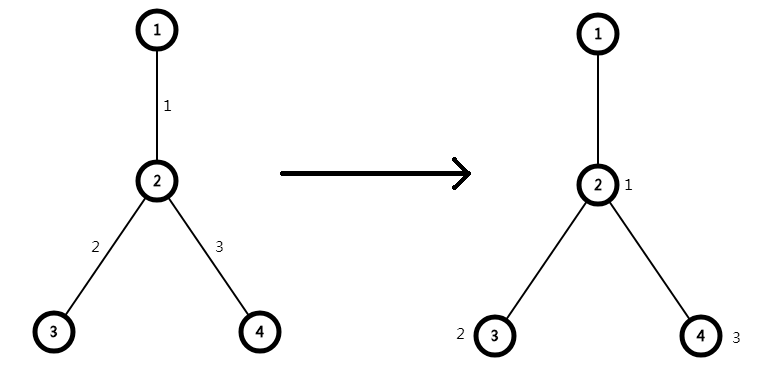

It is found that the point weight of our node is the edge weight connected to its edge, so if we want to modify or query the edge weight, what we modify or query is actually the point weight connected to its point,
Suppose we want to modify these two edges between 1-4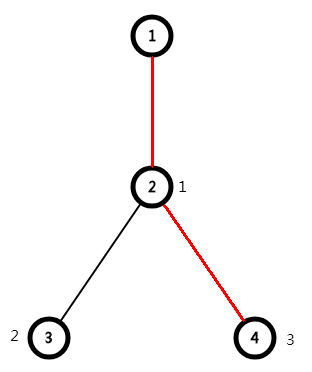

What we have changed is actually these two points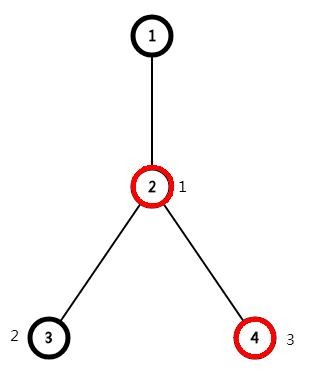

So when we modify or query on the chain, we do not need to modify or query nodes with shallow depth.

Then this is the problem on SPOJ. I don't know why I write c + + and hang it king I've only used c for my advice,%%

Code

#include <ctype.h>
#include <stdio.h>
#include <limits.h>
#include <stdlib.h>
#include <string.h>
#define lson rt << 1
#define rson rt << 1 | 1
#define N 10007
int t, n, m, num, cnt;
int head[N], a[N], w[N], son[N], size[N], f[N], top[N], dep[N], id[N], mx[N << 2];

class node {
    public :
        int nx, v, w;
} e[N << 2];

void add(int u, int v, int w) {
    e[++num].nx = head[u], e[num].v = v, e[num].w = w, head[u] = num;
}

int max(int a, int b) { return a > b ? a : b; }
#define swap(A, B)   \
    {                \
        int __T = A; \
        A = B;       \
        B = __T;     \
    }


void dfs1(int u, int fa) {
    size[u] = 1;
    for (int i = head[u]; ~i; i = e[i].nx) {
        int v = e[i].v;
        if (v != fa) {
            dep[v] = dep[u] + 1;
            f[v] = u;
            w[v] = e[i].w;  //Edge weight to point
            dfs1(v, u);
            size[u] += size[v];
            if (size[v] > size[son[u]]) son[u] = v;
        }
    }
}

void dfs2(int u, int t) {
    id[u] = ++cnt;
    a[cnt] = w[u];
    top[u] = t;
    if (son[u]) dfs2(son[u], t);
    for (int i = head[u]; ~i; i = e[i].nx) {
        int v = e[i].v;
        if (v != f[u] && v != son[u]) dfs2(v, v);
    }
}

void pushup(int rt) {
    mx[rt] = max(mx[lson], mx[rson]);
}

void build(int l, int r, int rt) {
    if (l == r) {
        mx[rt] = a[l];
        return ;
    }
    int m = (l + r) >> 1;
    build(l, m, lson);
    build(m + 1, r, rson);
    pushup(rt);
}

void update(int L, int c, int l, int r, int rt) {
    if (l == r) {
        mx[rt] = c;
        return ;
    }
    int m = (l + r) >> 1;
    if (L <= m) update(L, c, l, m, lson);
    else update(L, c, m + 1, r, rson);
    pushup(rt);
}

int query(int L, int R, int l, int r, int rt) {
    if (L <= l && r <= R) return mx[rt];
    int m = (l + r) >> 1, ans = -0x3f3f3f3f;
    if (L <= m) ans = max(ans, query(L, R, l, m, lson));
    if (R > m) ans = max(ans, query(L, R, m + 1, r, rson));
    return ans;
}

int query_chain(int x, int y) {
    int fx = top[x], fy = top[y], ans = -0x3f3f3f3f;
    while (fx != fy) {
        if (dep[fx] < dep[fy]) {
            swap(x, y);
            swap(fx, fy);
        }
        ans = max(ans, query(id[fx], id[x], 1, cnt, 1));
        x = f[fx], fx = top[x];
    }
    if (id[x] > id[y]) swap(x, y);
    ans = max(ans, query(id[x] + 1, id[y], 1, cnt, 1));
    /*Note here that ID [x] + 1 - > ID [y]
          Don't count the starting point
        */
    return ans;
}

int main() {
    scanf("%d", &t);
    while (t -- ) {
        num = cnt = 0;
        memset(head, -1, sizeof(head));
        memset(dep, 0, sizeof(dep));
        memset(id, 0, sizeof(id));
        memset(a, 0, sizeof(a));
        memset(w, 0, sizeof(w));
        memset(top, 0, sizeof(top));
        memset(size, 0, sizeof(size));
        memset(e, 0, sizeof(e));
        memset(mx, 0, sizeof(mx));
        memset(son, 0, sizeof(son));
        memset(f, 0, sizeof(f));
        scanf("%d", &n);
        for (int i = 1, x, y, z; i < n; ++i) {
            scanf("%d%d%d", &x, &y, &z);
            add(x, y, z), add(y, x, z);
        }
        dfs1(1, 0), dfs2(1, 1);
        build(1, n, 1);
        char s[20];
        int x, y;
        while (1) {
            scanf("%s", s);
            if (s[0] == 'D') break;
            else if (s[0] == 'C') {
                scanf("%d%d", &x, &y);
                x = dep[e[x << 1].v] > dep[e[(x << 1) - 1].v] ? e[x << 1].v : e[(x << 1) - 1].v;
                /*Here is to determine which point to modify*/
                update(id[x], y, 1, n, 1);
            } else {
                scanf("%d%d", &x, &y);
                printf("%d\n", query_chain(x, y));
            }
        }
    }
    return 0;
}