Previous period:
JAVA cultivation script Chapter 1: Painful torture
JAVA cultivation script Chapter 2: Gradual demonization
JAVA cultivation script Chapter 3: Jedi counterattack
JAVA cultivation script Chapter 4: "Closed door cultivation"
JAVA cultivation script Chapter 5: "Sleeping on firewood and tasting gall"
JAVA cultivation script Chapter 6: "Fierce battle"
JAVA cultivation script Chapter 7: Object oriented programming
JAVA cultivation script Chapter 8: String class
JAVA cultivation script Chapter 9: <List / ArrayList / LinkedList >
JAVA cultivation script Chapter 10: Priority queue (heap)
JAVA cultivation script (outside the fan chapter) Chapter 1: Can you really solve these four code problems
JAVA cultivation script (outside the fan chapter) Chapter 2: Library management system

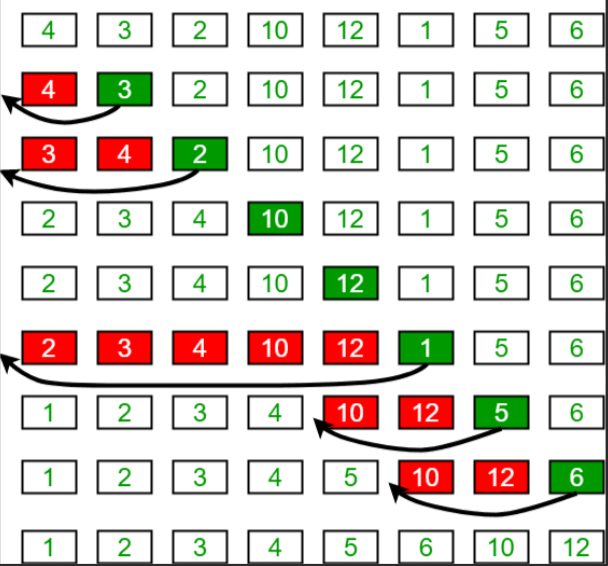
1, Insert sort
- Time complexity: O(n) ²).
- Space complexity: O(1).
- When a group of data is small and tends to be in order, it is recommended to use insert sorting
public static void InsertSort(int[] arr){
for(int i=1;i<arr.length;i++){
int tmp=arr[i];
int j=i-1;
for(;j>=0;j--){
if(arr[j]>tmp){
arr[j+1]=arr[j];
}else{
break;
}
}
arr[j+1]=tmp;
}
}
2, Half insert sort
- Time complexity: O(n) ²).
- Space complexity: O(1).
- Through direct insertion sorting, it can be found that the data before i subscript is orderly in each comparison.
- Half insertion sort uses this feature to binary search the value of i subscript and the previous ordered data.
- It is an optimization of direct insertion sorting.

public static void HalveInsertSort(int[] arr){
for(int i=1;i<arr.length;i++){
int left=0;
int right=i-1;
int tmp=arr[i];
while(right>=left){
int mid=(left+right)/2;
if(arr[mid]>tmp){
right=mid-1;
}else{
left=mid+1;
}
}
for(int j=i-1;j>right;j--){
arr[j+1]=arr[j];
}
arr[right+1]=tmp;
}
}
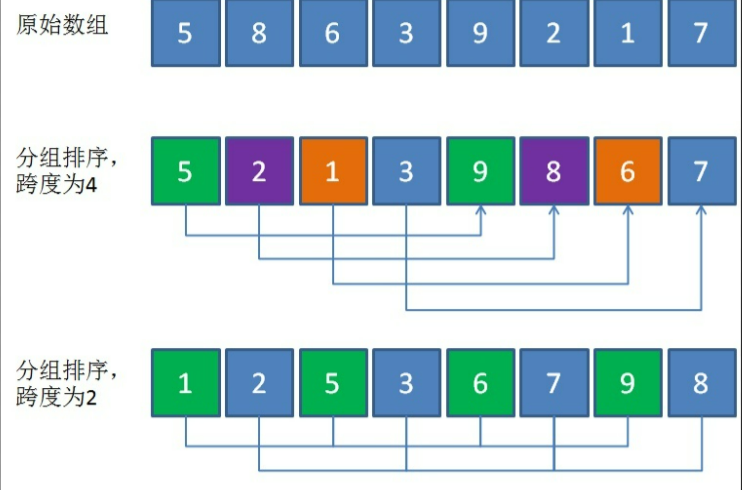
3, Hill sort
- Time complexity: O(n1.3).
- Space complexity: O(1).
- The subtlety of Hill sort is similar to that of insertion sort.
- The central idea is the value of gap. There are many methods of value, but they are similar, and the other ideas are not much different from the insertion sort.
public static void shellSort(int[] arr){
int gap=arr.length;
while(gap>0){
mySort(arr,gap);
gap/=2;
}
}
public static void mySort(int[] arr,int gap){
for(int i=gap;i<=arr.length;i++){
int tmp=arr[i];
int j=i-gap;
for(;j>=0;j-=gap){
if(arr[j]>tmp){
arr[j+gap]=arr[j];
}else{
break;
}
}
arr[j+gap]=tmp;
}
}
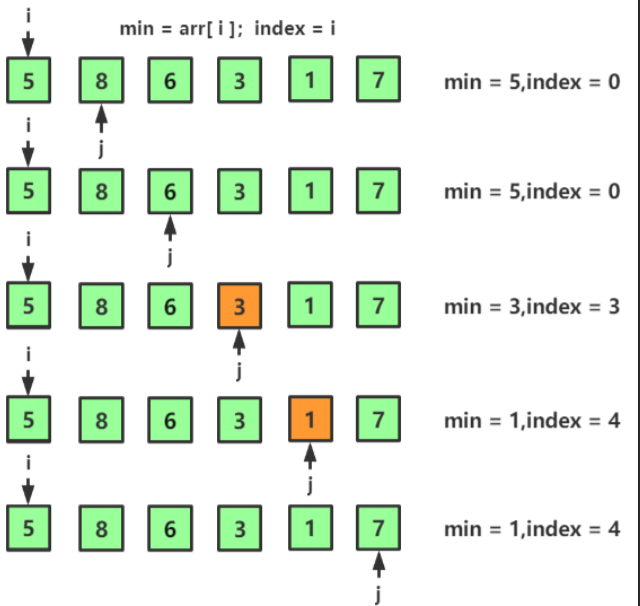
4, Select sort
- Time complexity: O(n) ²).
- Space complexity: O(1).
- As the name suggests, select sort, select and then sort.
- Each time, select a maximum or minimum data from the array to exchange with the head or tail.
- Then reduce the boundary after exchange.
public static void selectSort(int[] arr){
for(int i=0;i<arr.length;i++){
int max=0;
for(int j=1;j<arr.length-i;j++){
if(arr[j]>arr[max]){
max=j;
}
}
int tmp=arr[max];
arr[max]=arr[arr.length-1-i];
arr[arr.length-1-i]=tmp;
}
}
5, Bidirectional selection sorting
- Time complexity: O(n) ²).
- Space complexity: O(1).
- The same idea as selecting the sorting center is to find out the maximum and minimum at the same time
- In this algorithm, when the minimum subscript of each value is exchanged with a header subscript, if the position of the header subscript is just the maximum value, then the max subscript points to the minimum value instead of the maximum value after the exchange. The final if() judgment is very important.
public static void TwoWaySelectSort(int[] arr){
int left=0;
int right=arr.length-1;
while(left<=right){
int min=left;
int max=left;
for(int i=left+1;i<=right;i++){
if(arr[i]>arr[max]){
max=i;
}
if(arr[i]<arr[min]){
min=i;
}
}
swap(arr,min,left);
if(max==left){
max=min;
}
swap(arr,max,right);
left++;
right--;
}
}
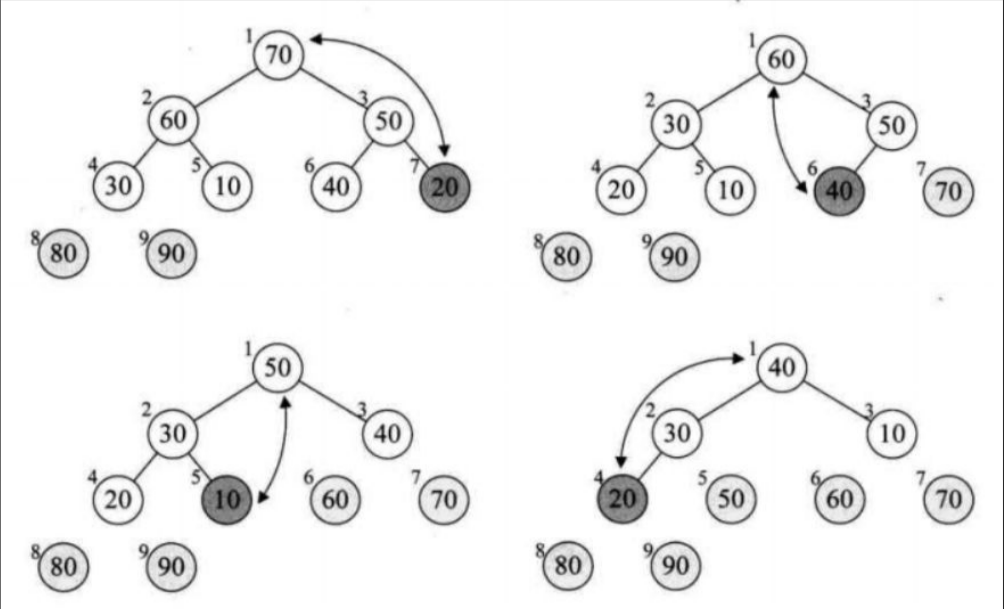
6, Heap sort
- Time complexity: O(logn).
- Space complexity: O(1).
- Suppose you want to sort in ascending order, first change the array into a heap storage form.
- Recirculation exchanges each element with the 0 subscript element from back to front.
- A lot of adjustments have to be made after each exchange.
public static void shiftDown(int[] arr,int parent,int len){
int child=parent*2+1;
while(child<len){
if(child+1<len&&arr[child]<arr[child+1]){
child++;
}
if(arr[child]>arr[parent]){
swap(arr,child,parent);
parent=child;
child=parent*2+1;
}else{
break;
}
}
}
public static void MySort(int[] arr){
for(int i=(arr.length-1)/2;i>=0;i--){
shiftDown(arr,i,arr.length);
}
}
public static void heapSort(int[] arr){
MySort(arr);
int end=arr.length-1;
while(end>0){
swap(arr,0,end);
shiftDown(arr,0,end);
end--;
}
}
7, Bubble sorting
- Time complexity: O(n) ²).
- Space complexity: O(1).
- Compare two by two, and finally put the largest element of the array in the last position.
- Adjust the boundary, because it is considered to be ordered after the last cycle, and the length of each comparison is - 1.
- If there is no data exchange after a cycle, it proves that the current data set is in order, and the cycle can be ended directly.

public static void bubbleSort(int[] arr){
for(int i=0;i<arr.length-1;i++){
boolean bool=true;
for(int j=0;j<arr.length-1-i;j++){
if(arr[j+1]<arr[j]){
swap(arr,j+1,j);
bool=false;
}
}
if(bool){
break;
}
}
}
8, Quick sort (digging)
- Time complexity: O(logn).
- Spatial complexity: O(logn).
- As the name suggests, select a benchmark value, put the value less than the benchmark value to the left and the value greater than the benchmark value to the right.

public static int partition(int[] arr,int start,int end){
int tmp=arr[start];
while(start<end){
while(start<end&&arr[end]>=tmp){
end--;
}
arr[start]=arr[end];
while(start<end&&arr[start]<=tmp){
start++;
}
arr[end]=arr[start];
}
arr[start]=tmp;
return start;
}
public static void quickSorts(int[] arr,int left,int right){
if(left>=right){
return;
}
int pivot=partition(arr,left,right);
quickSorts(arr,left,pivot-1);
quickSorts(arr,pivot+1,right);
}
public static void quickSort(int[] arr){
quickSorts(arr,0,arr.length-1);
}
9, Quick sort (Hoare)
- Time complexity: O(logn).
- Spatial complexity: O(logn).
- The idea is roughly the same as that of the pit excavation method. This method only exchanges each time greater than the reference value and less than the reference value at the same time.
public static int partition(int[] arr,int start,int end){
int i=start;
int j=end;
int tmp=arr[i];
while(i<j){
while(i<j&&arr[j]>=tmp){
j--;
}
while(i<j&&arr[i]<=tmp){
i++;
}
swap(arr,i,j);
}
swap(arr, start,i);
return i;
}
public static void quickSorts(int[] arr,int left,int right){
if(left>=right){
return;
}
int pivot=partition(arr,left,right);
quickSorts(arr,left,pivot-1);
quickSorts(arr,pivot+1,right);
}
public static void quickSort(int[] arr){
quickSorts(arr,0,arr.length-1);
}
10, Quick sort (non recursive)
- Time complexity: O(logn).
- Spatial complexity: O(logn).
- The non recursive idea needs a stack to record the subscripts around the reference value.
- The code running process is not much different from recursion.
public static int partition(int[] arr,int start,int end){
int tmp=arr[start];
while(start<end){
while(start<end&&arr[end]>=tmp){
end--;
}
arr[start]=arr[end];
while(start<end&&arr[start]<=tmp){
start++;
}
arr[end]=arr[start];
}
arr[start]=tmp;
return start;
}
public static void quickSort(int[] arr){
int left=0;
int right=arr.length-1;
Stack<Integer> stack=new Stack<>();
int pivot=partition(arr,left,right);
if(left+1<pivot){
stack.add(left);
stack.add(pivot-1);
}
if(right-1>pivot){
stack.add(pivot+1);
stack.add(right);
}
while(!stack.isEmpty()){
right=stack.pop();
left=stack.pop();
pivot=partition(arr,left,right);
if(left+1<pivot){
stack.add(left);
stack.add(pivot-1);
}
if(right-1>pivot){
stack.add(pivot+1);
stack.add(right);
}
}
}
11, Merge sort (recursive)
- Time complexity: O(n logn).
- Space complexity: O(n).
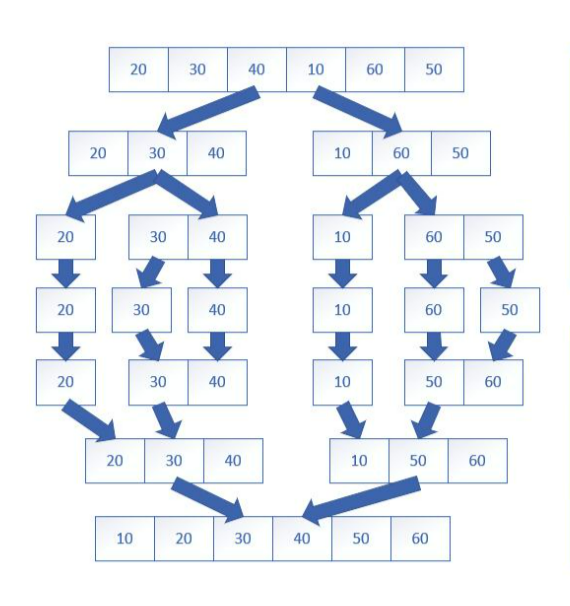
- Divide a big problem into small problems one by one, sort and combine each small problem.
public static void merge(int[] arr,int low,int mid,int high,int[] tmp){
int i = 0;
int j = low,k = mid+1;
while(j <= mid && k <= high){
if(arr[j] < arr[k]){
tmp[i++] = arr[j++];
}else{
tmp[i++] = arr[k++];
}
}
while(j <= mid){
tmp[i++] = arr[j++];
}
while(k <= high){
tmp[i++] = arr[k++];
}
for(int t=0;t<i;t++){
arr[low+t] = tmp[t];
}
}
public static void mergeSort(int[] arr,int low,int high,int[] tmp){
if(low<high){
int mid = (low+high)/2;
mergeSort(arr,low,mid,tmp);
mergeSort(arr,mid+1,high,tmp);
merge(arr,low,mid,high,tmp);
}
}
12, Merge sort (non recursive)
- Time complexity: O(nlogn).
- Space complexity: O(n).
- Just control the boundary.
public static void mergeSorts(int[] arr,int gap){
int s1=0;
int e1=s1+gap-1;
int s2=e1+1;
int e2=Math.min(arr.length-1,s2+gap-1);
int[] tmp=new int[arr.length];
int k=0;
while(s2<arr.length){
while(s1<=e1&&s2<=e2){
if(arr[s1]<=arr[s2]){
tmp[k++]=arr[s1++];
}else{
tmp[k++]=arr[s2++];
}
}
while(s1<=e1){
tmp[k++]=arr[s1++];
}
while(s2<=e2){
tmp[k++]=arr[s2++];
}
s1=e2+1;
e1=s1+gap-1;
s2=e1+1;
e2=Math.min(arr.length-1,s2+gap-1);
}
while(s1<=arr.length-1){
tmp[k++]=arr[s1++];
}
for(int i=0;i<k;i++){
arr[i]=tmp[i];
}
}
public static void mergeSort(int[] arr){
for(int gap=1;gap<arr.length;gap*=2){
mergeSorts(arr,gap);
}
}