Note: The following examples are sorted from small to large

Simple Selection Sorting

thought

The idea of simple selection sort is very simple. It divides a sequence to be sorted into two parts: the sorted part and the unsorted part. The sorted part is fixed, and the least element in the unsorted part is exchanged with its first element, and then the element is incorporated into the sorted part. The other elements operate the same way until only the last element is left in the unsorted part.
For example: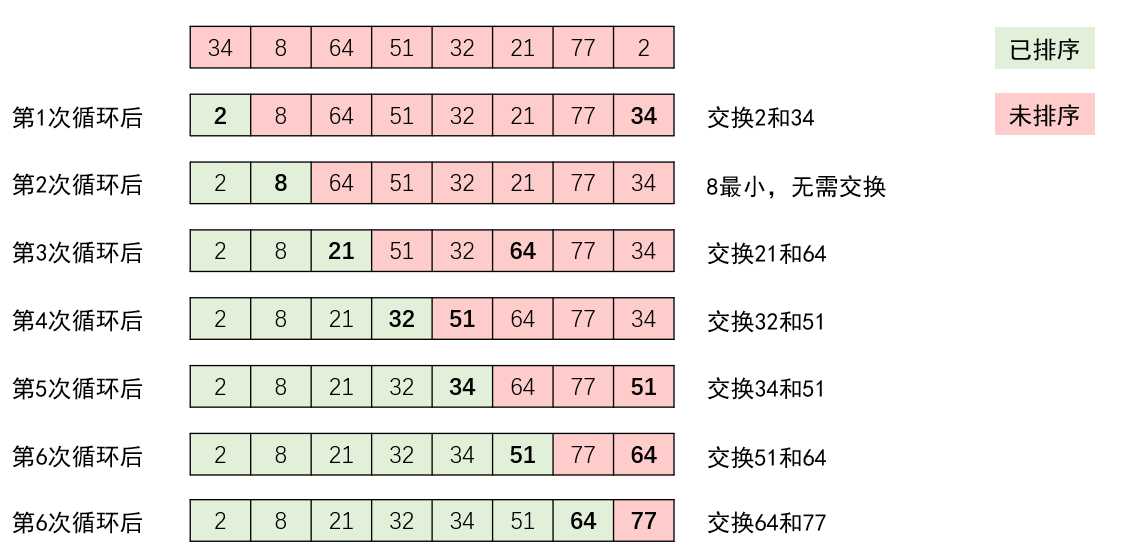

java code

class Sort{
	public static void main(String[] args) {
		int[] data = {34,8,64,51,32,21,77,2};
		selectSort(data);
		for(int x : data)
			System.out.print(x+" ");
		System.out.println();
	}
	public static void selectSort(int[] array) {
		for(int i=0; i<array.length-1; i++) {
			int minIdx = i;
			for(int j=i+1; j<array.length; j++) {
				if(array[j] < array[minIdx]) 
					minIdx = j;
			}
			if(minIdx != i)
				swap(array, i, minIdx);
		}
	}
	public static void swap(int[] array,  int i, int j) {
		int temp = array[i];
		array[i] = array[j];
		array[j] = temp;
	}
}

Heap sort

thought

Sort heaps from small to large:

1. Build a heap and a complete binary tree according to the data set.
2. If the heap is adjusted to a maximum heap, the top element is the largest number.
3. Exchange the top element of the stack and the last element of the current maximum heap;
4. Fixed the last element of the current heap, and the remaining elements still make up a heap (but not the largest heap)
5. Return 2 until the number of elements in the heap is 2.

At this point, the sorting ends.

The dynamic process can be referred to as video: https://www.bilibili.com/video/av18980178/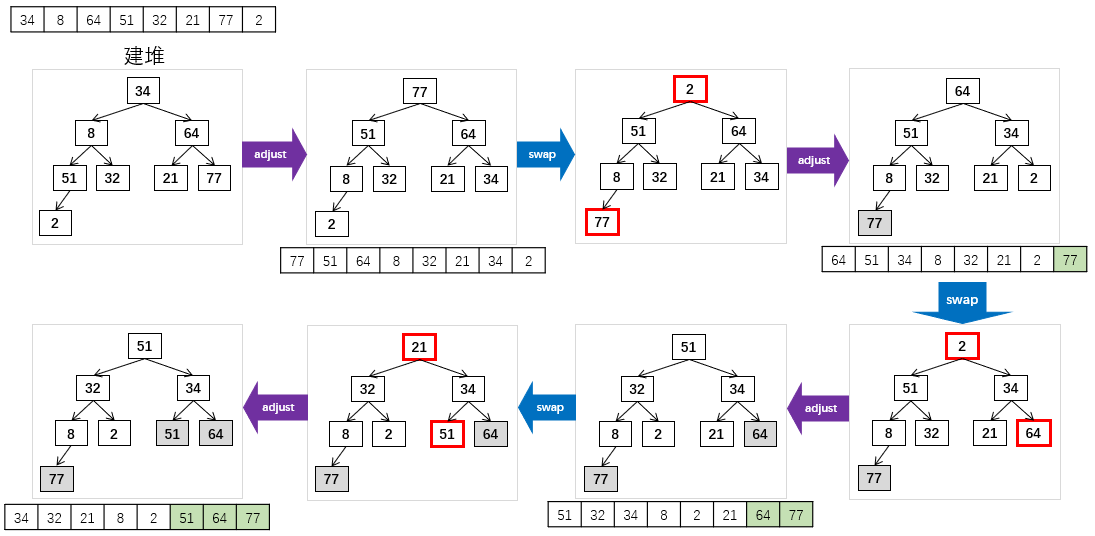

java code

class Sort{
	public static void main(String[] args) {
		int[] data = {34,8,64,51,32,21,77,2};
		heapSort(data);
		for(int x : data)
			System.out.print(x+" ");
		System.out.println();
	}
	public static void heapSort(int[] array) {
		int len = array.length;
		// Each time the maximum heap is adjusted, the root node is swapped with the last unadjusted node
		// Complete the sorting from back to front
		// Each adjustment is only for the unsorted part of the array, so the number of adjustments per time - 1
		for(int i=0; i<len-1; i++) {
			buildMaxHeap(array, len-1-i);
			swap(array, 0, len-1-i);
		}
	}
	public static void buildMaxHeap(int[] array, int lastIdx) {
		// Start with the parent of the last node
		for(int i=(lastIdx-1)/2; i>=0; i--) {
			int p = i;
			// Judge whether there is a left child at the current node, if there is an indication that it is not a leaf node
			while(p*2+1 <= lastIdx) {
				int left = 2*p + 1;
				int biggerIdx = left;
				// Right = left + 1
				if(left<lastIdx && array[left]<array[left+1])
					biggerIdx += 1;
				// If the child is larger than the father node, the larger child node and the father node are exchanged and adjusted downward.
				if(array[p]<array[biggerIdx]) {
					swap(array, p, biggerIdx);
					p = biggerIdx;
				}
				else
					break;
			}
		}
	}
	public static void swap(int[] array,  int i, int j) {
		int temp = array[i];
		array[i] = array[j];
		array[j] = temp;
	}
}