Skillfully solve mathematical problems

Using C + + to solve classical mathematical problems

1. Common multiples and common factors

Using the rolling division method, we can easily obtain the greatest common divisor (gcd) of two numbers; Multiply the two numbers and divide by the greatest common factor to obtain the least common multiple (LCM).
First, introduce the rolling division method:

#include<iostream>
#include<cstdio>
using namesapce std;

int fun(int m,int n)
{
    int rem;//Remainder, when the remainder is zero, the last m is the greatest common divisor
    //First use the smaller number to remainder the larger number, and then use the remainder to remainder the smaller number until the remainder is zero
    while(n>0)
    {
        rem=m%n;
        m=n;
        n=rem;
     }
     return m;//Return results
 }

int main(){
	int n,m;
	cin>>m>>n;
	cout<<"m and n The maximum common divisor of is:"<<fun(m,n)<<endl;
	return 0; 
}    

//Simplify it and find it with recursion
int fun(int m,int n)
{
    if(n==0) return m;
    return (fun(n,m%n);
}

//Simplify it again
int gcd(int m,int n){
    return n ? gcd(n,m%n):m;
}

Solution:

int gcd(int a,int b)
{
    return b==0 ? a:gcd(b,a%b);
}
int lcm(int a,int b)
{
    return a*b/gcd(a,b);
}

Furthermore, we can also obtain the coefficients x and y of a and B by extending the Euclidean algorithm (extended gcd), so that ax + by = gcd(a, b).

int xGCD(int a,int b,int &x,int &y)
{
    if(!b){
        x=1,y=0;
        return 0;
    }
    int x1,y1,gcd=xGCD(b,a%b,x1,y1);
    x=y1,y=x1-(a/b)*y1;
    return gcd;
}

2. Prime number

Prime numbers, also known as prime numbers, refer to natural numbers that have no other factors except 1 and itself in natural numbers greater than 1. It is worth noting that each number can be decomposed into the product of prime numbers.

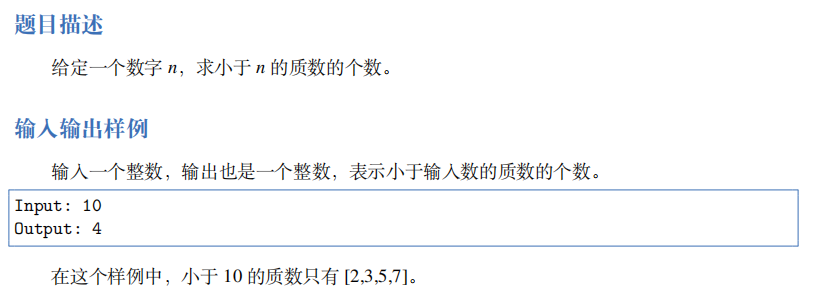
The Sieve of Eratosthenes is a very common method to judge whether an integer is a prime number. And it can judge the integer less than n when judging an integer n, so it is very suitable for this problem. Its principle is also very easy to understand: traverse from 1 to N. assuming that the current traverse reaches m, mark all integers less than N and multiple of m as sums; After traversal, numbers that are not marked as sum are prime numbers.

int countPrimes(int n)
{
    if(n<=2) return 0;
    vector<bool>prime(n,true);
    int count=n-2;//Remove 1 which is not prime
    for(int i=2;i<=n;++i)
    {
        if(prime[i]){
            for(int j=2*i;j<n;j+=i)
            {
                if(prime[i]){
                    prime[j]=false;
                    --count;
                }
            }
        }
    }
    return count;
}

Using some properties of prime numbers, we can further optimize the algorithm

int countPrimes(int n)
{
    if(n<=2) return 0;
    vector<bool>prime(n,true);
    int i=3,sqrtn=sqrt(n),count=n/2;//Even numbers must not be prime numbers
    while(i<=sqrtn)//The minimum prime factor must be less than or equal to the square
    {
        for(int j=i*i;j<n;j+=2*i)//Avoid even and repeated traversals
        {
            if(prime[j])
            {
                --count;
                prime[j]=false;
            }
        }
        do{
            i+=2;
        }while(i<=sqrtn&&!prime[i]);//Avoid even and repeated traversals
    }
    return count;
}           

3. Digital processing

The problem of binary conversion type is usually calculated by division and modulus (mod). At the same time, we should also pay attention to some details, such as negative numbers and zero. If the output is numeric rather than string, you also need to consider whether it will exceed the upper and lower bounds of integers.

string convertToBase7(int num)
{
    if(num==0) return "0";
    bool is_negative=num<0;
    if(is_negative) num= -num;
    string ans;
    while(num)
    {
        int a=num/7,b=num%7;
        ans=to_string(b)+ans;
        num=a;
    }
    return is_negative ? "-" + ans: ans;
}

Topic 1:
Given a nonnegative integer, judge how many zeros are at the end of its factorial result.

Each trailing 0 consists of 2 × 5 = 10, so we can divide each element of factorial into prime numbers and multiply them, and count the number of 2
And 5. Obviously, the number of quality factor 2 is much more than that of quality factor 5, so we can only count the number of quality factors in the factorial result
Factor 5.

int trailingZeros(int n)
{
    return n==0 ? 0:n/5+trailingZeros(n/5);
}

Topic 2: given two strings composed of numbers, find the result of their addition

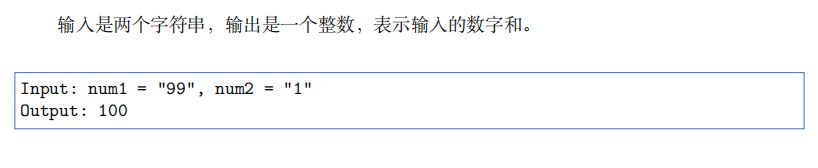
Because the addition operation is carried out from back to front, you can flip the string first and then calculate it bit by bit. This type of question examines the details, such as carry, digit difference and so on.

string addStrings(string num1,string num2)
{
    string output("");
    reverse(num1.begin(),num1.end());
    reverse(num2.begin(),num2.end());
    int onelen=num1.length(),twolen=num2.length();
    if(onelen<=twolen)
    {
         swap(num1,num2);
         swap(onelen,twolen);
     }
     int addbit;
     for(int i=0;i<twolen;++i)
     {
         int cur_sum=(num1[i]-'0')+(num2[i]-'0')+addbit;
         output+=tot_string((cur_sum)%10);
         addbit=cur_sum<10?0:1;
     }
     for(int i=twolen;i<onelen;++i)
     {
         int cur_sum=(num1[i]-'0')+addbit;
         output+=to_string((cur_sum)%10);
         addbit=cur_sum<10?0:1;
     }
     if(addbit)
     {
         output+="1";
     }
     reverse(output.begin(),output.end());
     return output;
 }

Topic 3: judge whether a number is to the power of 3

There are two methods. One is to use logarithm. Let log3n = m, if n is an integer power of 3, then M must be an integer.

bool isPowerOfThree(int n){
    return fmod(log10(n)/log10(3),1)==0;
}

Another method is that because the maximum power of 3 in the range of int is 319 = 116261467, if n is an integer power of 3, then the remainder of 116261467 divided by N must be zero; vice versa.

bool isPowerOfThree(int n)
{
    return n>0&&1162261467%n==0;
}

4. Random and sampling

Given an array, it is required to implement two instruction functions. The first function "shuffle" can randomly disrupt the array, and the second function "reset" can restore the original order.

We use the classic Fisher Yates shuffle algorithm. The principle is to achieve random disorder by randomly exchanging positions. There are two writing methods: forward and reverse, and the implementation is very convenient. Note the implementation details of the "reset" function and the constructor of the class.

class Solution{
    vector<int>origin;
public:
    Solution(vector<int>nums):origin(std::move(nums)){}

    vector<int>reset(){
        return origin;
    }
    
    vector<int>shuffled(){
        if(origin.empty()) return {};
        vector<int>shuffled(origin);
        int n=origin.size();
        //You can use reverse or forward shuffle with the same effect
        //Reverse shuffle:
        for(int i=n-1;i>=0;--i)
        {
            swap(shuffles[i],shuffled[rand()%(i+1)]);
        }
        //Forward shuffle
        //for(int i=0;i<n;++i){
        //    int pos=rand()%(n-i);
        //    swap(shuffled[i],shuffled[i+pos]);
        //}
        return shuffled;
    }
};  

Topic 1:
Given an array, each position of the array represents the weight of the position, which requires random sampling according to the probability of the weight

The input is a one-dimensional positive integer array, representing the weight; And a one-dimensional array containing instruction strings, indicating how many random samples are run. The output is a one-dimensional array of integers, representing the position of randomly sampled integers in the array.

We can use partial first_ Sum sums the prefixes (i.e. the sum of all numbers up to each position). This result is monotonically increasing for a positive integer array. Whenever sampling is needed, we can first randomly generate a number, and then use the dichotomy to find its position in the prefix and to simulate the process of weighted sampling. The dichotomy here can be used as lower_bound implementation. Taking the example, the prefix sum of weight array [1,3] is [1,4]. If the number we randomly generate is 1, then lower_ The position returned by bound is 0; If the number we randomly generate is 2, 3, 4, then lower_ The position returned by bound is 1.

class Solution{
    vector<int>sums;
public:
    Solution(vector<int>weights):sums(std::move(weights)){
        partial_sum(sums.begin(),sums.end(),sums.begin());
    }
    int pickIndex(){
        int pos=(rand()%sums.back())+1;
        return lower_bound(sums.begin(),sums.end(),pos)-sums.begin();
    }
};

Topic 2:
Given a one-way linked list, it is required to design an algorithm that can randomly obtain one of the numbers.

Unlike arrays, we cannot know the total length of the linked list before traversing the linked list. Here we can use reservoir sampling: traverse the linked list once. When traversing the m-th node, we have a probability of 1m to select this node to overwrite the previous node selection.

class Solution{
    ListNode*head;
public:
    Solution(ListNode*n):head(n){}
    int getRandom(){
        int ans=head->val;
        ListNode*node=head-<next;
        int i=2;
        while(node){
            if((rand()%i)==0){
                ans=node->val;
            }
            ++i;
            node=node->next;
        }
        return ans;
    }
}