Simple Problem with Integers

You have N integers, A1, A2, ... , AN. You need to deal with two kinds of operations. One type of operation is to add some given number to each number in a given interval. The other is to ask for the sum of numbers in a given interval.

Input

The first line contains two numbers N and Q. 1 ≤ N,Q ≤ 100000.
The second line contains N numbers, the initial values of A1, A2, ... , AN. -1000000000 ≤ Ai ≤ 1000000000.
Each of the next Q lines represents an operation.
"C a b c" means adding c to each of Aa, Aa+1, ... , Ab. -10000 ≤ c ≤ 10000.
"Q a b" means querying the sum of Aa, Aa+1, ... , Ab.

Output

You need to answer all Q commands in order. One answer in a line.

Sample Input

10 5
1 2 3 4 5 6 7 8 9 10
Q 4 4
Q 1 10
Q 2 4
C 3 6 3
Q 2 4

Sample Output

4
55
9
15

The main idea of the title is that there are n integers. If you input CLRX, add a value x to all elements in the L-R interval.
Input QLR is the sum of all elements in the output L-R interval.
Because the data range is very large, if we use for loop, we can use segment tree to maintain the interval sum, and change the interval value. First of all, look at this graph.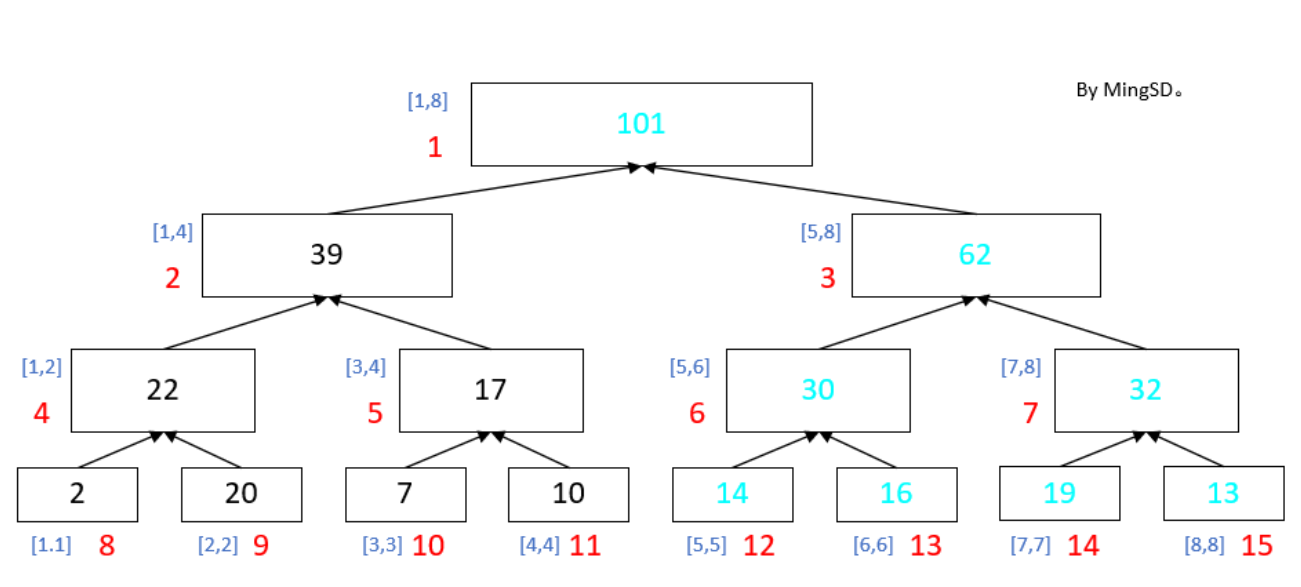

Similar to a binary tree, each point becomes an interval, the top one is the initial root interval, each time divided into the following two intervals left son interval and right son interval. We use a sum array to record the interval sum, then the value of each point is the lowest leaf interval (L equals R), which is a point, we. Every time we need to do is to use the given range X and y to query in the existing range LR. First your L-R and X-Y intervals intersect, we can perform the operation, but it may not all contain, so we need to recursive query, and then the line segment tree has a magic thing is the lazy tag, which is what, every update, we do not. You have to add X to every element, maybe just x to that interval.*(
R-L+), we can use a lazy record, not downloaded values, because we already know the interval sum, so we do not need to continue downloading, save time, and for the next query, when we want to use an interval, first of all, to determine whether there is value in the lazy tag of this location, if we download, this is pushdown. Function,

void pushdown(int o,int l)
{
    if(add[o])
    {
        add[o*2]+=add[o];
        add[o*2+1]+=add[o];
        sum[o*2]+=add[o]*(l-l/2);
        sum[o*2+1]+=add[o]*(l/2);
        add[o]=0;
    }
}

For each interval, we have sum[o]=sum[o2]+sum[o2+1]; each father interval equals the sum of two sons interval.
We build trees recursively.

void build(int l,int r,int o)
{
    if(l==r){scanf("%lld",&sum[o]);return;}
    int mid=(l+r)/2;
    build(l,mid,o*2);
    build(mid+1,r,o*2+1);
    sum[o]=sum[o*2]+sum[o*2+1];
}

Maintenance and update of intervals every time

void update(int l,int r,int x,int y,int c,int o)
{
    if(l>=x&&r<=y)
    {
        sum[o]+=(ll)c*(r-l+1);
        add[o]+=c;
        return ;
    }
    int mid=(l+r)/2;
    pushdown(o,r-l+1);
    if(mid>=x) update(l,mid,x,y,c,o*2);
    if(mid<y) update(mid+1,r,x,y,c,o*2+1);
    sum[o]=sum[o*2]+sum[o*2+1];
}

When mid >= x indicates that there are elements that need to be updated in the left son interval of the interval. When mid < y, there are elements that need to be updated in the right son interval. We inquire into the interval every time. We add the interval value to the value of this section x, and then store the value in the lazy tag, and judge whether there are values before lazy. If there are, it indicates that there are values that need to be updated in the past. Download, then we call the pushdown function (mentioned above) for download.
It's easy to understand the following query interval sum.

ll query(int l,int r,int x,int y,int o)
{
    if(l>=x&&r<=y) return sum[o];
    pushdown(o,r-l+1);
    int mid=(l+r)/2;
    ll sum=0;
    if(mid>=x)sum=query(l,mid,x,y,o*2);
    if(y>mid) sum+=query(mid+1,r,x,y,o*2+1);
    return sum;
}

This is just a simple template to maintain the interval and sum, there are various templates, but it is only a template, after understanding these, we can really start to learn (I think, because the real problems encountered, the future can not be solved by the template, so there is still a long way to go, go on refueling, it is useless to say more, I am sorry to be unable to resist a wave of nonsense. )
Complete code:

#include<stdio.h>
typedef long long ll;
const int maxn=400010;
ll add[maxn],sum[maxn];
void build(int l,int r,int o)
{
    if(l==r){scanf("%lld",&sum[o]);return;}
    int mid=(l+r)/2;
    build(l,mid,o*2);
    build(mid+1,r,o*2+1);
    sum[o]=sum[o*2]+sum[o*2+1];
}
void pushdown(int o,int l)
{
    if(add[o])
    {
        add[o*2]+=add[o];
        add[o*2+1]+=add[o];
        sum[o*2]+=add[o]*(l-l/2);
        sum[o*2+1]+=add[o]*(l/2);
        add[o]=0;
    }
}
void update(int l,int r,int x,int y,int c,int o)
{
    if(l>=x&&r<=y)
    {
        sum[o]+=(ll)c*(r-l+1);
        add[o]+=c;
        return ;
    }
    int mid=(l+r)/2;
    pushdown(o,r-l+1);
    if(mid>=x) update(l,mid,x,y,c,o*2);
    if(mid<y) update(mid+1,r,x,y,c,o*2+1);
    sum[o]=sum[o*2]+sum[o*2+1];
}
ll query(int l,int r,int x,int y,int o)
{
    if(l>=x&&r<=y) return sum[o];
    pushdown(o,r-l+1);
    int mid=(l+r)/2;
    ll sum=0;
    if(mid>=x)sum=query(l,mid,x,y,o*2);
    if(y>mid) sum+=query(mid+1,r,x,y,o*2+1);
    return sum;
}
int main()
{
    int q,n,l,r,c;
    char x;
    scanf("%d%d",&n,&q);
    build(1,n,1);
    while(q--)
    {
        scanf(" %c",&x);
        if(x=='Q')
        {
            scanf("%d%d",&l,&r);
            printf("%lld\n",query(1,n,l,r,1));
        }
        else
        {
            scanf("%d%d%d",&l,&r,&c);
            update(1,n,l,r,c,1);
        }
    }
}