preface

shufflenetV1 is another direction of the development of convolutional neural network to lightweight, which is the lightweight network following Mobilenet.

1, Paper reading summary

Paper address
Tricks: application of group revolution on 1 * 1 convolution; channel shuffle improves information transmission between channels;

1.Channel Shuffle

In ResNeXt, only the group convolution mode of 33 convolution is considered, so that most of the computation is focused on 11 convolution (pointwise conv). Therefore, this paper also adopts group convolution for 1 * 1 convolution to ensure that each convolution operation only acts on a small number of channels, ensure the sparsity of channel connection and reduce the amount of calculation.
What is group convolution?
Suppose that the output feature map of the upper layer has n, that is, the number of channels is channel=N, that is, the upper layer has n convolution cores. Then suppose the number of groups m of group convolution. Then, the operation of the group volume layer is to divide the channel into M parts first. Each group corresponds to N/M channels, which are connected independently. Then, after each group convolution is completed, the outputs are concatenate d as the output channel of this layer.

2.Group Conv

If the group convolution method is adopted in the whole network, the output characteristic diagram of each channel is only related to the characteristic diagram of a few input channels, resulting in information blocking. Therefore, it is necessary to divide N (number of channels) input feature maps into multiple subgroups, select different feature maps from the subgroups to form a new subgroup and send it to the next group for convolution, as shown in Figure 1.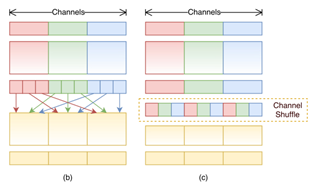

3. Ablation Experiment

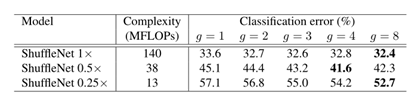
1) Number of channels of group convolution (g=1,2,3,4,8)
Using group convolution on 1 * 1 convolution is better than not. In some models (such as ShuffleNet 0.5 ×)， When the number of groups becomes large (e.g. g= 8), the classification score reaches saturation or even decreases. As the number of groups increases (and therefore wider feature mapping), the input channels of each convolution filter become fewer, which may impair the representation ability. For smaller models, such as ShuffleNet 0.25 ×， Group numbers tend to get better results, indicating that larger feature maps bring more benefits to smaller models.

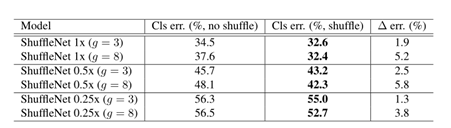
2) Compare shuffle and no shuffle:
The channel shuffle can improve the classification score under different settings, especially when the number of groups is large (such as g= 8), the performance of the channel random model is obviously better than that of the similar model, which shows the importance of cross group information exchange.

2, Code implementation

Code reference

1.shuffle implementation

The code is as follows:

class shuffle(nn.Module):
    def __init__(self,group=2):
        super(shuffle, self).__init__()
        self.group=group
    def forward(self,x):
        """shuffle Operation:[N,C,H,W] -> [N,g,C/g,H,W] -> [N,C/g,g,H,w] -> [N,C,H,W]"""
        num,channel,height,width=x.size()
        x=x.view(num,self.group,channel//self.group,height,width)
        x=x.permute(0,2,1,3,4)
        x=x.reshape(num,channel,height,width)
        return x

2. Bottleneck module implementation

The code is as follows:

class bottleblock(nn.Module):
    def __init__(self,in_channel,out_channel,stride,group):
        super(bottleblock, self).__init__()
        self.stride=stride
        if in_channel==24:
            group=1
        else:
            group=group
        self.conv1_with_group=nn.Sequential(nn.Conv2d(in_channels=in_channel,out_channels=out_channel//4,kernel_size=1,stride=1,groups=group,bias=False),
                                            nn.BatchNorm2d(out_channel//4),
                                            nn.ReLU(inplace=True))
        self.shuffle=shuffle(group)
        self.conv2_with_depth=nn.Sequential(nn.Conv2d(in_channels=out_channel//4,out_channels=out_channel//4,stride=stride,kernel_size=3,groups=out_channel//4,padding=1,bias=False),
                                            nn.BatchNorm2d(out_channel//4))
        self.conv3_with_group=nn.Sequential(nn.Conv2d(in_channels=out_channel//4,out_channels=out_channel,kernel_size=1,stride=1,groups=group),
                                            nn.BatchNorm2d(out_channel))
        if stride==2:
            self.shortcut=nn.AvgPool2d(stride=stride,kernel_size=3,padding=1)
        else:
            self.shortcut=nn.Sequential()
    def forward(self,a):
        x=self.conv1_with_group(a)
        x=self.shuffle(x)
        x=self.conv2_with_depth(x)
        x=self.conv3_with_group(x)
        residual=self.shortcut(a)
        if self.stride==2:
            return F.relu(torch.cat([x,residual],1))
        else:
            return F.relu(residual+x)

3.shufflenet network implementation

The code is as follows:

class shufflenet(nn.Module):
    def __init__(self,num_class,group):
        super(shufflenet, self).__init__()
        self.num_class=num_class
        self.inchannel=24
        if group==8:
            stage_dict={'bolck_num':[4,8,4],
                         'outchannel':[384,768,1536],
                         'group':group}
        elif group==4:
            stage_dict = {'bolck_num': [4, 8, 4],
                               'outchannel': [272, 544, 1088],
                               'group': group}
        elif group==3:
            stage_dict = {'bolck_num': [4, 8, 4],
                               'outchannel': [240, 480, 960],
                               'group': group}
        elif group==2:
            stage_dict = {'bolck_num': [4, 8, 4],
                               'outchannel': [200, 400, 800],
                               'group': group}
        elif group==1:
            stage_dict = {'bolck_num': [4, 8, 4],
                               'outchannel': [144, 288, 576],
                               'group': group}
        block_num=stage_dict['bolck_num']
        outchannel=stage_dict['outchannel']
        group=stage_dict['group']
        self.initial=nn.Sequential(nn.Conv2d(kernel_size=3,padding=1,in_channels=3,out_channels=24,stride=2),
                                   nn.BatchNorm2d(24),
                                   nn.ReLU(inplace=True),
                                   nn.MaxPool2d(kernel_size=3,stride=2,padding=1))

        self.layer1 = self.make_layer(block_num[0],outchannel[0],group)
        self.layer2 = self.make_layer(block_num[1], outchannel[1], group)
        self.layer3 = self.make_layer(block_num[2], outchannel[2], group)

        self.pool=nn.AdaptiveAvgPool2d(1)
        self.fc=nn.Linear(outchannel[2],num_class)
    def make_layer(self,block_num,outchannel,group):
        layer_list=[]
        for i in range(block_num):
            if i==0:
                stride=2
                catchannel=self.inchannel
            else:
                stride=1
                catchannel=0
            layer_list.append(bottleblock(self.inchannel,outchannel-catchannel,stride,group))
            self.inchannel=outchannel
        return nn.Sequential(*layer_list)
    def forward(self,x):
        x=self.initial(x)
        x=self.layer1(x)
        x=self.layer2(x)
        x=self.layer3(x)
        x=self.pool(x)
        x=x.view(x.size(0),-1)
        x=self.fc(x)
        return F.softmax(x,dim=1)

summary

This paper introduces the core idea and code implementation of shuffleNetV1 for communication and discussion!
Previous review:
(1)Interpretation of CBAM paper + pytoch implementation of CBAM resnext
(2)Interpretation of SENet paper and code examples
Forecast for next period:
shuffleNet-V2 paper reading and code implementation