Topic address: https://nanti.jisuanke.com/t/41412

Title:

2 < n < 3000 to satisfy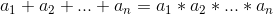Number of rankings

 

Ideas for solving problems:

It can be determined by simple typing (n < 10).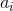An arrangement (= n) that must exist is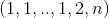So the maximum product is 2n.

Multiple Set Arrangement Formula: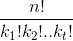In fact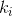Represents the number of times each number is repeated, and n is the total number of numbers.

dfs enumerates the number of occurrences of 2-3000 digits in the whole sequence (there are at most 13 2 in 2*3000, so the number of occurrences of each digit is very small). The total number of occurrences is num, the product is mul, and sum. Then the number of occurrences of 1 in the sequence meeting the requirements of the title is num1=mul-sum, and only when num1 is greater than 0 & num1 + num < 3000 can a sequence satisfying the conditions be determined. Column n n n=num1+num, and then use multiple set permutation formula to calculate the number of permutations.

Note: Arrangement is a division form, there will be a denominator larger than the molecule after taking the model, need to use the inverse element.

 

ac Code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll mod = 1e9+7;
const ll maxn = 3005;
int t, n;
ll f[maxn], INV[maxn], ans[maxn];
ll qpow(ll a, ll b)
{
    ll ans = 1;
    a = a % mod;
    while(b)
    {
        if(b&1) ans = ans * a % mod;
        a = a*a % mod;
        b >>= 1;
    }
    return ans;
}
bool dfs(ll x, ll mul, ll sum, ll num, ll inv)//num: Number of non-1 digits
{
    if(x==1)
    {
        ll num1 = mul - sum;
        if(num1 >= 0 && num+num1 <= 3000)
        {
            ans[num+num1] = (ans[num+num1] + ((f[num+num1]*inv)%mod * INV[num1])%mod)%mod;
            return true;
        }
        else return false;
    }
    dfs(x-1, mul, sum, num, inv);//NO x
    for(int i = 1; mul*pow(x,i) <= 2*3000; i++)//6000 max. 2 ^ 13
    {
        bool flag = dfs(x-1, mul*pow(x,i), sum+x*i, num+i, INV[i]*inv%mod);//i is the number of times x appears
        if(!flag) break;
    }
    return true;
}
int main()
{
    //freopen("/Users/zhangkanqi/Desktop/11.txt","r",stdin);
    f[0] = 1;
    for(int i = 1; i <= 3000; i++) f[i] = f[i-1] * i % mod;
    for(int i = 0; i <= 3000; i++) INV[i] = qpow(f[i], mod-2);//Inverse elements, the number may be 0, also need to deal with INV[0]
    dfs(3000, 1, 0, 0, 1);
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d", &n);
        printf("%lld\n", ans[n]);
    }
    return 0;
}