Bubble Sort

• Picture presentation:

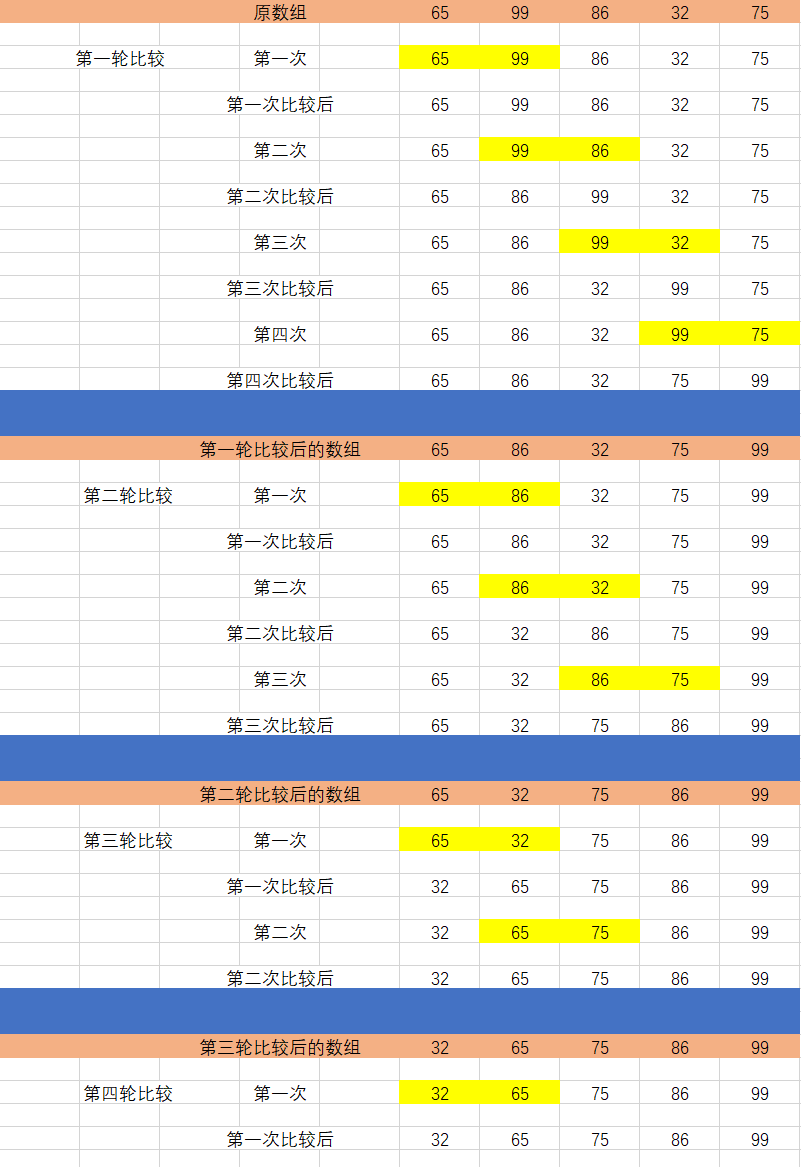
• Description:

• Compare the size of two adjacent numbers. If the former is larger than the latter, exchange them

• Perform the same operation on each pair of adjacent elements from beginning to end, from the first pair at the beginning to the last pair at the end, so that the operation can put the maximum number on the far right

• Code implementation:

package com.zcs.lession08.paixu;
/**
 * Bubble sorting
 * */
public class MaoPaoDemo {
	public static void main(String[] args) {
		int[] a = { 65, 99, 86, 32, 75 };
		
		//Bubble sorting formula
		//Outer circulation n-1
		for (int i = 0; i < a.length-1; i++) {
			//Inner circulation n-1-i
			for (int j = 0; j < a.length-1-i; j++) {
				//The current value is compared with the next value
				if(a[j+1]<a[j]) {
					//The current value is larger than the latter value, and the two values are exchanged
					int temp = a[j];
					a[j] = a[j+1];
					a[j+1]=temp;
				}
			}
		}
		//Loop traversal output
		for (int i : a) {
			System.out.print(i+"\t");
		}
	}
}

• Core code analysis:

It can be seen from the picture demonstration:

Four rounds of comparison were conducted:

• 4 times in the first round
• 3 times in the second round
• The third round twice
• Once in the fourth round

// Round i of outer cycle control comparison
for (int i = 0; i < a.length-1; i++) {
			//The inner loop controls the number of comparisons in each round, and a larger value will be compared in each round		
			for (int j = 0; j < a.length-1-i; j++) {
                // If the following number is less than the previous number, it will be exchanged
				if(a[j+1]<a[j]) {
					int temp = a[j];
					a[j] = a[j+1];
					a[j+1]=temp;
				}
			}
		}

Outer layer cycle a.length-1: the outer layer comparison round can be controlled as length, which will be more efficient than one round

Inner layer loop a.length-1-i: controls the number of inner layer comparisons

Selection Sort

Picture presentation:

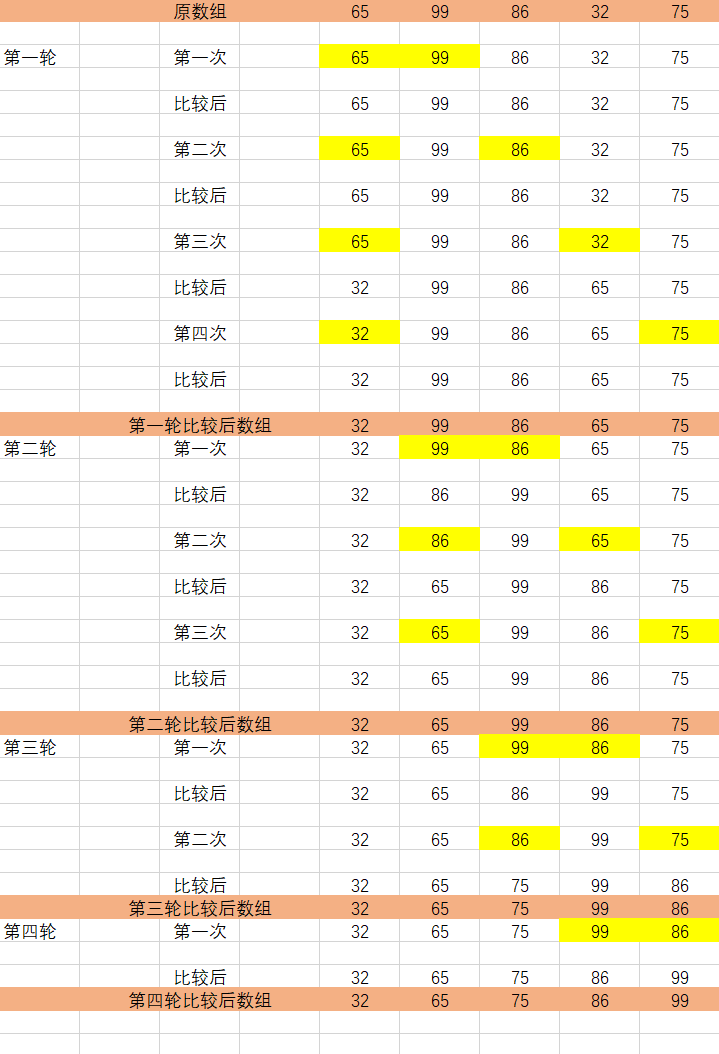
describe

First, find the smallest element in the unordered array and store it at the beginning of the sorted array. Any element that has never been completely sorted will find the second smallest element and put it at the end of the sorted array, and so on

code implementation

package com.zcs.lession08.paixu;
/**
 * Select sort
 * */
public class XuanZeDemo {
	public static void main(String[] args) {
		int[] a = { 65, 99, 86, 32, 75 };
		// Select sort
		// Outer circulation-1
		for (int i = 0; i < a.length - 1; i++) {
			// Each time, use the subscript of i as the benchmark value for comparison, and start comparison with the next value
			// So j starts the loop from i+1. In order not to exceed the array subscript, the inner loop does not need - 1
			int min = i;//Define a subscript that finds the smallest decimal point
			for (int j = i + 1; j < a.length; j++) {
				// Judge to find the minimum number 		 The inner loop finds the minimum number
				if (a[j] < a[min]) {
					min = j;
				}
			}
			//If the subscript of the lowest decimal point is not the defined subscript, it is exchanged
			if (min != i) {
				exchange(a, min, i);
			}
		}
		for (int i : a) {
			System.out.print(i + "\t");
		}

	}
	//Exchange method
	public static void exchange(int[] num, int a, int b) {
		int temp = num[a];
		num[a] = num[b];
		num[b] = temp;
	}
}

Core code analysis

It can be seen from the picture demonstration:

Four rounds of comparison were conducted:

• 4 times in the first round
• 3 times in the second round
• The third round twice
• Once in the fourth round

	for (int i = 0; i < a.length - 1; i++) {
			// Each time, use the subscript of i as the benchmark value for comparison, and start comparison with the next value
			// So j starts the loop from i+1. In order not to exceed the array subscript, the inner loop does not need - 1
			int min = i;//Define a subscript that finds the smallest decimal point
			for (int j = i + 1; j < a.length; j++) {
				// Judge to find the minimum number 		 The inner loop finds the minimum number
				if (a[j] < a[min]) {
					min = j;
				}
			}
			//If the subscript of the lowest decimal point is not the defined subscript, it is exchanged
			if (min != i) {
				exchange(a, min, i);
			}
		}
		for (int i : a) {
			System.out.print(i + "\t");
		}

	}
public static void exchange(int[] num, int a, int b) {
		int temp = num[a];
		num[a] = num[b];
		num[b] = temp;
	}
}

The exchange() static method calls the minimum value found in every outer loop in the loop, and puts it into a sorted array by static method.

Outer cycle a.length-1 because the round is based on the subscript of i

Inner loop a.length because j starts from i+1, in order not to exceed the subscript, the - 1 operation is not required

A decimal subscript is defined within the outer loop

The inner loop traverses all the numbers, and takes the decimal mark of the smallest number in the outer loop for comparison

If the minimum number defined by the inner loop and the outer loop is inconsistent, the values are exchanged