First, before explaining the segment tree, you should understand that the segment tree should be a tool that can change the time complexity of O(N) into o (logN) for modifying and maintaining intervals (or segments).

1, Introduction of segment tree concept

Segment tree is a binary tree, that is, for a segment, we will use a binary tree to represent it. For example, a line segment with a length of 5 can be expressed as follows:

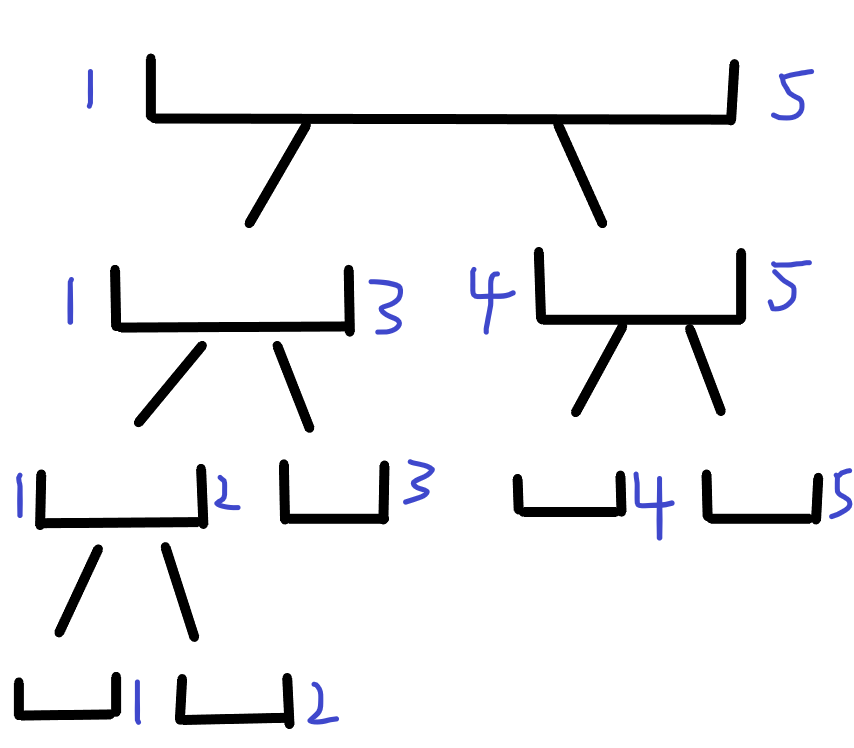
This means that if you want to represent the sum of segments, the weight of the top root node is equal to the sum of the weights of the two son nodes.
Then we can get: the weight of node i = the weight of the left son of node i + the weight of the right son of node I.
Then we can build a tree according to this result, and set a structure array tree, tree[i].l and tree[i].r represent the left and right ranges of the line segment respectively.
The left and right child node numbers of the binary tree are equal to the current node numbers 2 and 2 + 1.
Then we can get: tree [i]. Sum = tree [I < < 1]. Sum + tree [I < < 1 | 1]. Sum.

inline ll ls(ll i) { return i << 1;}
inline ll rs(ll i) { return i << 1 | 1;}

inline void build(ll i, ll l, ll r)   //Recursive tree building	
{
	if (l == r)  //This node is a leaf node
	{
		tree[i].sum = a[l];
		return;
	}

	ll mid = (l + r) >> 1;

	build(ls(i), l, mid);   //Left child
	build(rs(i), mid + 1, r);   //Right child
	push_up(i);  //Update sum of current node
}

When we build a segment tree, we usually have only four nodes of the data size.

2, Simple segment tree

1. Interval query, single point modification

First, what are we going to do with a segment tree? In fact, the segment tree, as its name suggests, is used to maintain a segment or interval. For example, if you want to find the sum of 23 ~ 500 elements in an interval of 1 ~ 1000, the simple method is to iterate over and add for loops. This can certainly be solved, but it is too slow.
Therefore, we need to come up with a new method, line segment tree can solve this problem well.
OK, let's take the picture just now as an example and attach values of 1, 2, 3, 4 and 5 to its leaf nodes
Then we draw the following figure according to the logic of building trees just now.

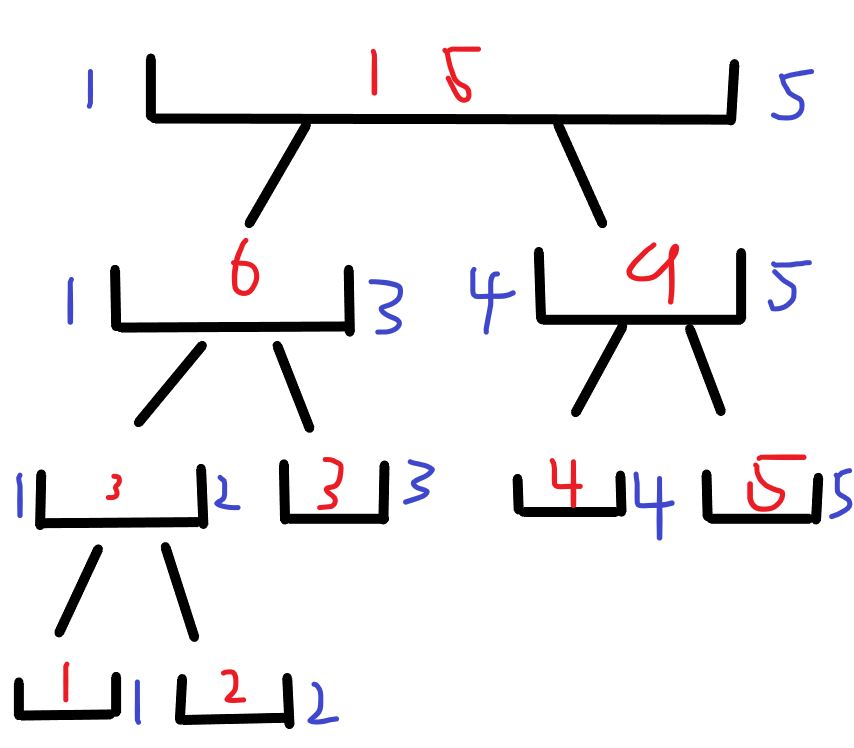
Now, let's take a data to simulate interval query. For example, we now want to get the sum of the weights of all elements in the 1 ~ 4 interval (that is, interval query).
1. To get the sum of 1 ~ 4 intervals, we first query from the root node and find that its left child 1 ~ 3 is related to it.
2. We find that its left child 1 ~ 3 is completely contained by it, so we directly return the value of 1 ~ 3. And return to the 1 ~ 5 range
3. When we get to the interval 4 ~ 5, we find that this interval is also related to it, so we come to the interval 4 ~ 5.
4. We found that the left child 4 ~ 4 in the interval 4 ~ 5 is related to the answer interval. Then we return the value of the interval 4 ~ 4 to the beginning.
5. Then we start by creating a t variable with an initial value of 0
Let's summarize the query method of segment tree:

1. If this interval is completely included in the target interval, the value of this interval is returned directly
2. If the left son of this interval intersects with the target interval, search for the left son
3. If the right son of this interval intersects with the target interval, search for the right son

That's how it's written in Code:

ll query(ll q_x, ll q_y, ll l, ll r, ll i)
{
	ll t = 0;

	if (q_x <= l && r <= q_y) return tree[i].sum;

	ll mid = (l + r) >> 1;

	if (q_x <= mid) t += query(q_x, q_y, l, mid, ls(i));
	if (q_y > mid) t += query(q_x, q_y, mid + 1, r, rs(i));

	return t;
}

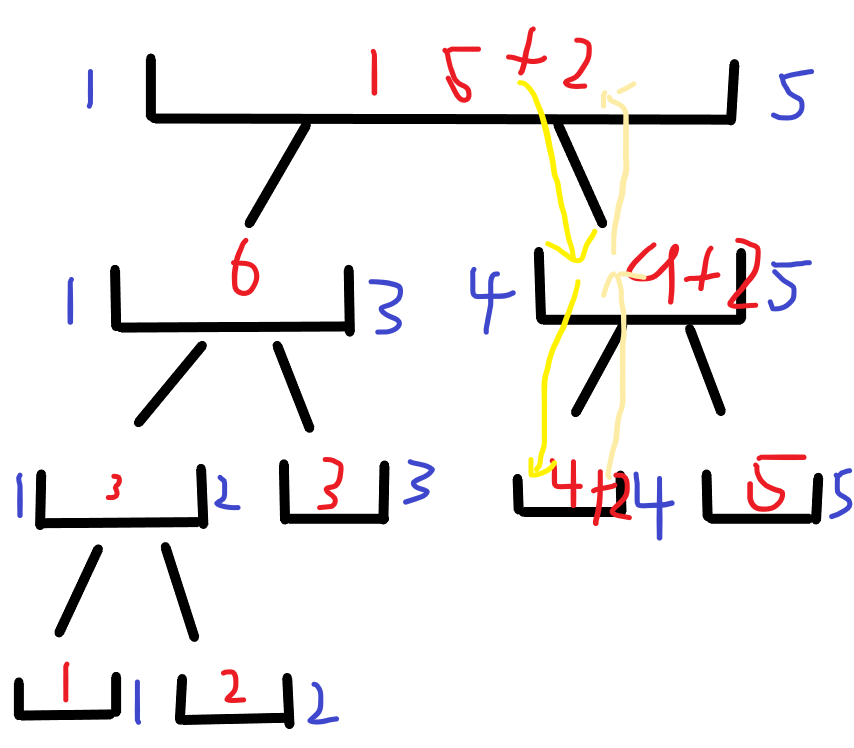
Next, let's explain how to implement single point modification.
First, because only the weight of one point is modified, you only need to add k to the weight of the dis bit of the interval.
Then, starting from the root node, see whether the dis point is in the left son or the right son. Just run wherever you are. Finally, when you return, do tree [i]. Sum = tree [I < < 1]. Sum + tree [I < < 1 | 1]. Sum

Let's have a picture to help understand. Yellow represents the path to go, and light yellow represents the path to return.

That's how it turns into code:

inline void update(int xl, int k, int l, int r, int i)
{
    if(l == r)    //The leaf node adds the value to the original sum
    {
        tree[i].sum += k;
        return;
    }

    int mid = q(l , r);

    if(xl <= mid)        //This point runs to the left son on the left
    {
        update(xl, k, l, mid, ls(i));
    }
    else        //Or run to the right
    {
        update(xl, k, mid + 1, r, rs(i));
    }

    push_up(i);    //Update weights
    return;
}

2. Interval modification, single point query

For interval modification and single point query, our idea becomes: if you add k to this interval, it is equivalent to painting this interval with a k mark. Then, when you single point query, you run from top to bottom and add up the marks along the road.

The method of labeling an interval is similar to the above interval search. The principle is the same as the three above, except the first one: if the interval is completely included in the target interval, directly return the value of the interval to if the interval. If the interval is completely included in the target interval, mark the interval k

That's how it's written in Code:

inline void update(ll i, ll xl, ll yr, ll l, ll r, ll k){
    if(xl <= l && yr >= r){//If this interval is completely included in the target interval, say the interval mark k
        tree[i].sum+=k;
        return ;
    }

	ll mid = (l + r) >> 1;

    if(mid >= l)
        update(ls(i), xl, yr, l, mid, k);
    if(mid + 1 <= r)
        update(rs(i), xl, yr, mid + 1, r, k);
}

Then there is the single point query, which is better understood, that is, where dis runs, just add all the bid prices on the path:

void query(ll i,ll l, ll r, ll dis){
    ans += tree[i].num;//All the way up
    
    if(l == r) return ;
    
	ll mid = (l + r) >> 1;

    if(dis <= mid)
        query(ls(i), l, mid, dis);
    if(dis >= mid + 1)
        query(rs(i), mid + 1, r, dis);
}

3, Interval + / - modification and interval query

Before starting, it is inevitable to ask: is there any difference between interval modification and single point modification? Why introduce it separately?
The answer is not wrong. Although both of them are modified, if we modify the interval according to the idea just now, there will be errors.
Let's take a chestnut: if you want to add 2 to the value of interval 1 ~ 3, according to the idea of single point modification, we find that we return after reaching interval 1 ~ 3, but we should add 2 to each element of this interval. Then such an idea can't be realized.

Now that this problem has arisen, we must find a way to solve it.
The next step is to introduce the lazy tag and push_ The down operation is the solution. push_down is actually the operation to apply the lazy flag.

So let's see how the lazy tag solves this problem.
By analyzing single point modification and interval modification, we find that interval modification may stop recursion in advance, and the operation that should have changed the child node of this point has not been realized. That's the problem.
Then let's think that leaf nodes are related to their parent nodes, and their parent nodes are related to their parent nodes. In this way, we think that since there is a connection, we use a tag to record the modification value, and then pass it layer by layer. In this way, when we get the answer interval, it has a lazy mark, indicating that the interval has changed its value.
When querying, you need to pass this table record down.
Through the operation just now, we can solve this problem. That's how we write code

inline void f(ll i, ll l, ll r, ll k)   //Update the value of the child node with the lazy flag
{
	tree[i].lazy = tree[i].lazy + k;
	tree[i].sum = tree[i].sum + k * (r - l + 1);
}

inline void push_down(ll i, ll l, ll r)   //Pass lazy tag to child node
{
	ll mid = (l + r) >> 1;

	f(ls(i), l, mid, tree[i].lazy);
	f(rs(i), mid + 1, r, tree[i].lazy);
	tree[i].lazy = 0;    //Remember to set zero after passing
}

inline void update(ll xl, ll xr, ll l, ll r, ll i, ll k)   //Interval modification
{
	if (xl <= l && r <= xr)    //If the modified interval contains this node interval, it will be updated directly
	{
		tree[i].sum += k * (r - l + 1);
		tree[i].lazy += k;
		return;
	}
	push_down(i, l, r);   //Pass lazy tag to child node

	ll mid = (l + r) >> 1;

	if (xl <= mid) update(xl, xr, l, mid, ls(i), k);
	if (xr > mid) update(xl, xr, mid + 1, r, rs(i), k);

	push_up(i);   //Remember to pass information up
}

ll query(ll q_x, ll q_y, ll l, ll r, ll i)    //Interval query
{
	ll t = 0;

	if (q_x <= l && r <= q_y) return tree[i].sum;

	ll mid = (l + r) >> 1;

	push_down(i, l, r);  Pass lazy tag to child node
	if (q_x <= mid) t += query(q_x, q_y, l, mid, ls(i));
	if (q_y > mid) t += query(q_x, q_y, mid + 1, r, rs(i));

	return t;
}

4, Interval multiplication and division modification and query

1. Multiplicative segment tree

If the line segment tree has only multiplication, just make tree[i].lazy = k, and then tree[i].sum = k. But if you add and multiply, it's different.
When we pass lazy down, we need to consider whether to add or multiply first. In fact, the solution is very simple. We only need to divide the lazy into two, one is the plz of addition and the other is the mlz of multiplication.
mlz is very simple to handle. You only need to push_ When down, it's OK to directly the father's, but adding requires adding the original plz, the father's mlz and the father's plz.

Next is the code:

inline void pushdown(ll i,ll l, ll r){//Note that long must be enabled for data of this level
    ll k1=tree[i].mlz,k2=tree[i].plz;

	ll mid = (l + r) >> 1;

    tree[ls(i)].sum=(tree[ls(i)].sum*k1+k2*(mid - l+1))%p;
    tree[rs(i)].sum=(tree[rs(i)].sum*k1+k2*(r - mid + 1 + 1))%p;
    tree[ls(i)].mlz=(tree[ls(i)].mlz*k1)%p;
    tree[rs(i)].mlz=(tree[rs(i)].mlz*k1)%p;
    tree[ls(i)].plz=(tree[ls(i)].plz*k1+k2)%p;
    tree[rs(i)].plz=(tree[rs(i)].plz*k1+k2)%p;
    tree[i].plz=0;
    tree[i].mlz=1;
    return ;
}

2. Root segment tree

First of all, we should know that the division of c + + is rounding down. Obviously, (a+b)/k= a/k+b/k (in the case of rounding down), and the root sign, obviously, the root sign (a) + the root sign (b)= Root sign (a+b) so what?

The first idea is violence. For each interval l~r to be changed, divide each point separately, but the time complexity will be slower than that of large violence (because of multiple constants), so how to optimize?

For each interval, we maintain its maximum and minimum values. Then, each time we modify it, if the root of the maximum value of the interval is the same as the root of the minimum value, it means that the overall root of the interval will not produce error, so we can modify it directly (the same is true for division)
Among them, lazytage regards division as subtraction, and records the value subtracted by each element in this interval.

The code is as follows:

inline void Sqrt(int i, int lx, int yr, int l, int r){
    if(l >= lx && r<=yr && (tree[i].minn - (long long)sqrt(tree[i].minn)) == (tree[i].maxx - (long long)sqrt(tree[i].maxx))){//If the maximum and minimum of this interval are the same
        long long u = tree[i].minn - (long long)sqrt(tree[i].minn);//Calculate the amount to subtract from each element in the interval
        tree[i].lz += u;
        tree[i].sum -= (tree[i].r-tree[i].l+1)*u;
        tree[i].minn -= u;
        tree[i].maxx -= u;
            //cout<<"i"<<i<<" "<<tree[i].sum<<endl;
        return ;
    }
    if(r < lx || l > yr)  return ;
    push_down(i);

	ll mid = (l + r) >> 1;

    if(mid >= l)  Sqrt(ls(i), lx, yr, l, mid);
    if(mid + 1 <= r)  Sqrt(rs(i), lx, yr, mid + 1, r);
    tree[i].sum = tree[ls(i)].sum+tree[rs(i)].sum;
    tree[i].minn = min(tree[ls(i)].minn,tree[rs(i)].minn);//Maintain maximum and minimum values
    tree[i].maxx = max(tree[ls(i)].maxx,tree[rs(i)].maxx);
    //cout<<"i"<<i<<" "<<tree[i].sum<<endl;
    return ;
}

Then there is no change in pushdown. Just remember - lazytage for tree[i].minn and tree[i].maxx.