Link: 4441: Necklace

Solution: there are only ten middle numbers that can be used as middle numbers. Then we enumerate the middle numbers, DP from left to right, enumerate the breakpoints, and maintain the maximum answer.

The transfer equation is also good to think about:

DP1 [i] = max {DP1 [J] | J < I, a[i] < a [J]} + a[i] (right half)

DP2 [i] = max {DP2 [J] | J > I, a[i] < a [J]} + a[i] (left half)

Obviously, this DP needs to be accelerated by line tree or tree array. Tree array is easier to write, and its complexity is \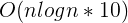

AC Code:

template<class T> inline T qmax(T a, T b) { return a > b ? a : b; }

int n;
int a[maxn<<1], b[maxn], c[maxn];
int dp1[maxn], dp2[maxn];

int getmax(int x){
	int ret = 0;
	for( ; x > 0; ret = qmax(ret,  c[x]), x -= lowbit(x));
	return ret;
}

void update(int x, int val){
	for ( ; x <= maxn; c[x] = qmax(c[x], val), x += lowbit(x));
}

int ans = 0;

void solve(int pos){
	int tot = 0;
	rep(i, pos + 1, pos + n - 1){
		if(a[i] != 10000) b[++tot] = a[i];
	}
	memset(c, 0, sizeof(c));
	dp1[0] = 0;
	rep(i, 1, tot){
		int t = getmax(10000 - b[i]);
		dp1[i] = max(dp1[i-1], t + b[i]);
		update(10000 - b[i], t + b[i]);
	}
	memset(c, 0, sizeof(c));
	dp2[tot+1] = 0;
	Rep(i, tot, 1){
		int t = getmax(10000 - b[i]);
		dp2[i] = max(dp2[i+1], t + b[i]);
		update(10000 - b[i], t + b[i]);
	}
	int Max = 0;
	rep(i, 1, tot){
		Max = qmax(Max, dp1[i] + dp2[i+1]);
	}
	ans = max(ans, Max + 10000);
}

int main()
{
	while(~scanf("%d", &n)){
		ans = 0;
		rep(i, 1, n) scanf("%d", a + i), a[n+i] = a[i];
		rep(i, 1, n){
			if(a[i] == 10000) solve(i);
		}
		printf("%d\n", ans);
	}
	return 0;
}

Of course, the line tree can also be written, but the constant is larger (and it's not easy to knock on the court)

template<class T> inline T qmax(T a, T b) { return a > b ? a : b; }

int a[maxn<<1], b[maxn];
int dp1[maxn], dp2[maxn];
int n;

struct node{
	int l, r, Max;
}tree[maxn<<2];

void push_up(int i){
	tree[i].Max = qmax(tree[lson].Max, tree[rson].Max);
}

void build(int i, int l, int r){
	tree[i].l = l, tree[i].r = r;
	if(l == r) { tree[i].Max = 0; return ; }
	int mid = (l + r) >> 1;
	build(lson, l, mid);
	build(rson, mid + 1, r);
	push_up(i);
}

void update(int i, int pos, int val){
	if(tree[i].l == pos && tree[i].r == pos) { tree[i].Max = val; return ; }
	tree[i].Max = qmax(tree[i].Max, val);
	int mid = (tree[i].l + tree[i].r) >> 1;
	if(pos <= mid) update(lson, pos, val);
	else update(rson, pos, val);
}

int Query(int i, int l, int r){
	if(tree[i].l == l && tree[i].r == r) return tree[i].Max;
	int mid = (tree[i].l + tree[i].r) >> 1;
	if(r <= mid) return Query(lson, l, r);
	else if(l > mid) return Query(rson, l, r);
	else {
		int ta = Query(lson, l, mid);
		int tb = Query(rson, mid + 1, r);
		return qmax(ta, tb);
	}
}

int ans = 0;

void solve(int pos){
	int tot = 0;
	rep(i, pos + 1, pos + n - 1){
		if(a[i] != 10000) b[++tot] = a[i];
	}
	build(1, 1, 10000);
	dp1[0] = 0;
	rep(i, 1, tot){
		int t = Query(1, 1, 10000 - b[i]);
		dp1[i] = max(dp1[i-1], t + b[i]);
		update(1, 10000 - b[i], t + b[i]);
	}
	build(1, 1, 10000);
	dp2[tot+1] = 0;
	Rep(i, tot, 1){
		int t = Query(1, 1, 10000 - b[i]);
		dp2[i] = max(dp2[i+1], t + b[i]);
		update(1, 10000 - b[i], t + b[i]);
	}
	int Max = 0;
	rep(i, 1, tot){
		Max = qmax(Max, dp1[i] + dp2[i+1]);
	}
	ans = max(ans, Max + 10000);
}

int main()
{
	while(~scanf("%d", &n)){
		ans = 0;
		rep(i, 1, n) scanf("%d", a + i), a[n+i] = a[i];
		rep(i, 1, n){
			if(a[i] == 10000) solve(i);
		}
		printf("%d\n", ans);
	}
	return 0;
}

over