Portal

Title Description:

A restaurant has N dishes, No. 1...n. The evaluation value of the i-dish is AI (1 < = I < = n). There are m customers, the expectation value of the ith customer is Bi, and his preference value is xi. Therefore, the ith customer thinks that the delicious degree of the j dish is bi XOR (aj+xi), XOR represents exclusive or operation.

The ith customer wants to pick out the most delicious dish from these dishes, that is, the dish with the most delicious value. However, due to the price and other factors, he can only choose from the li to ri. Please help them find the most delicious food.

Crap:

The first time I saw XOR, I thought of building a dictionary tree. I wanted to directly build a persistent dictionary tree... But I found that there was an addition, and I didn't know how to solve this problem. At last, I looked at the general meaning of the solution to the problem, and then I typed it myself, but the answer was not right all the time. I was crazy about debugging, and I found out that I did some bit calculation...

Solution ideas:
There is XOR operator on the title, if it has CodeForces - 923C In order to find exclusive or value, we need to start from high position to low position.
In the same way, we start from this idea. We regard a+x as a number (set as the variable ans). If we look for the i-th position of b,
Then we must have determined all the bits higher than i.
Let's say that now we have reached the i-th position. If b is 0, then in order to make ans^b larger, ans is better to be 1 in this position,
So what is the scope of ans? In fact, that is，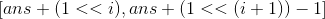
So if b is 1 at this time, then in order to make ans^b bigger, ans is better to be 0,
So the value range of ans is，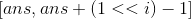
Our ans=a+x, our a range is ans-x. We use the established persistent line segment to query whether there are satisfied conditions.

The big men of the valley: https://www.luogu.org/problemnew/solution/P3293

See code for details:

#include<bits/stdc++.h>

using namespace std;
const int maxn = 2e5 + 5;

struct node {
    int ls, rs, cnt;
#define left(a, b) p[a].ls, p[b].ls, l, mid
#define right(a, b) p[a].rs, p[b].rs, mid + 1, r
} p[maxn * 40];
int root[maxn], times;

void insert(int &now, int old, int l, int r, int x) {
    now = ++times;
    p[now] = p[old], p[now].cnt++;
    if (l == r) return;
    int mid = (l + r) >> 1;
    if (x <= mid) insert(left(now, old), x);
    else insert(right(now, old), x);
}

int query(int sta, int end, int l, int r, int a, int b) {
    if (l == a && r == b) return p[end].cnt - p[sta].cnt;
    int mid = (l + r) >> 1;
    if (b <= mid) return query(left(sta, end), a, b);
    else if (a > mid) return query(right(sta, end), a, b);
    else return query(left(sta, end), a, mid) + query(right(sta, end), mid + 1, b);
}

int solve(int x) {
    return min(max(0, x), maxn);
}

int main() {
    int n, m, a, b, x, l, r;
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a);
        insert(root[i], root[i - 1], 0, maxn, a);
    }
    while (m--) {
        scanf("%d %d %d %d", &b, &x, &l, &r);   ///     b^(a+x)
        int ans = 0;            ///ans=a+x
        for (int i = 17; i >= 0; i--) {
            int L, R;
            if (b >> i & 1) {       //If bit i of b is 1
                L = solve(ans - x), R = solve(ans - x + (1 << i) - 1);
                if (query(root[l - 1], root[r], 0, maxn, L, R))     //If there is a+x, the i-th bit is 0
                    continue;                                       //ans does not count (1 < < I)
                ans |= (1 << i);
            } else {                //If bit i of b is 0
                L = solve(ans + (1 << i) - x), R = solve(ans + (1 << i + 1) - 1 - x);
                if (query(root[l - 1], root[r], 0, maxn, L, R))     //If i of a+x is 1
                    ans |= (1 << i);
            }
        }
        printf("%d\n", ans ^ b);
    }
    return 0;
}