This article is based on thinking about an interesting question, in another of my blog posts.< An Interesting 5 X 5 Square Matrix Painting Problem > It is described in detail. Given its conclusion, as a programmer, I still want to use this problem as a starting point to write a path-finding algorithm that can traverse all possible routes, as an exercise to learn graph-related algorithms. If you are interested in that original question, click on the article link above and go out and turn right.
I. Review of Problems
_or to briefly describe the problem: there is a 5 X 5 dot matrix, as shown below, if you want to use a brush to connect all the blue dots, there is a feasible route. Three requirements need to be met:
The strokes must be horizontal or vertical.
_2. The strokes should not go beyond the boundary of the square matrix.
_3. Each point passes only once, and yellow dots are not allowed to pass through.
The mathematical proof of this problem has been given in the opening article, and I will not elaborate on it here. Only its algorithm implementation is considered here.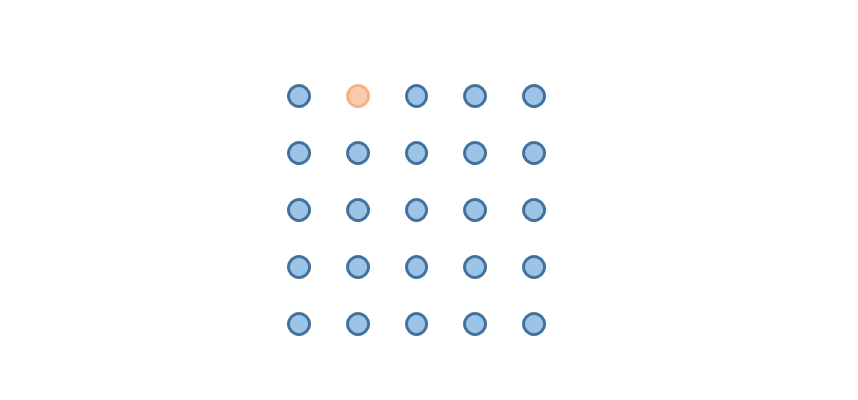
_Before thinking about algorithms, we need to make abstract analysis of the problems. We can understand the above problems as follows:
2. Abstract Analysis
_Since the problem has been proved mathematically that no route can meet the requirements of the problem, the purpose of the algorithm is not to find the so-called required route, but to traverse all the routes that can be formed from the starting point to the grid. It can be assumed that the above grid is a map, Xiaoming students walk in the grid according to the map, the purpose is to find out all the routes from the starting point to all points. Xiao Ming first specifies coordinates in the map, the bottom of the grid as the x-axis, the left vertical side as the y-axis, then the red pentagonal coordinates are (1,4). Xiao Ming started from the origin. At the beginning, all the intersections on the map were marked as "not passed". Xiaoming randomly chooses the next point. If he passes through (0,0), (1,0), (1,1), (2,1), (2,2), (3,2), (4,2), (4,1), (4,0), (3,0), (3,1) in turn, he will mark the corresponding position of the map as he goes forward. When he came to (3,1), because the surrounding (2,1), (3,2), (4,1) had already passed, there was no way to go forward, so he could only step back. Before going back, Xiao Ming wrote down the line in his notebook and marked it as a historical line. Then he went back. One step back, Xiaoming will erase the mark "past" and change it to "not past" at the place where he left, because he can take that position the next time he goes from another route. When retreating to (3,0), (3,1) the position will be changed from "past" to "not past", and the adjacent (2,0) has not been passed, so it will not retreat and turn to (2,0). When we arrived at (2,0), there was no way to go, so we recorded the current route, then went back and marked the map. When we go back to (3,0), although we will find that (3,1) is "untouched", but if we go (3,1), we will find that this route has already appeared in the history of notebooks, so we still can't go back (3,1). We will continue to go back according to this principle until we start from the beginning. Xiao Ming will eventually return to the starting point when he reaches all the routes on the map. At this point, the list of historical routes in his notebook is all the routes from the beginning to all the points on the map.
3. Algorithmic Analysis
_Considering the implementation of the algorithm, this obviously uses the "graph" in the data structure. Every route attempt is a depth traversal of the graph. What the algorithm needs to do is to select the starting point randomly and then traverse the new route continuously in depth. Every step forward, the new location is put on the stack. It should be noted here that for every attempt, when there is no way to go, it does not mean that all 24 points have been traversed, because according to the rules, the reason for no way to go may be that all the positions around the current point (hereinafter referred to as "neighbors") have been passed, that is, they are already in the stack, or walking. It's at the corner. So what should we do when there is no way to go? Should we start from the beginning again, or what? In theory, it works, but considering the efficiency, that is to say, let the algorithm do as little repetitive things as possible, I choose to record the current route (an array of point sequences) when there is no way to go (stored in a set, which records all historical routes), and then return and bounce off the position from the stack. Out, each retreat will record the current route as a historical route, until there is a "point not in the stack" around, no retreat, but to a new position. At this time, the last retreat of the historical route determines the direction of the next will not follow this route. (If N steps are successively retreated, the most recent retreat is a subset of the previous N-1 retreat. Continue in the above way, because the "map" is limited, when all possible routes are out of date, will eventually return to the starting point. At this point, the list of historical routes sets records all routes from the starting point to all points on the map.
4. Algorithmic description:
Input: A two-dimensional array M[26][5]. (The first dimension corner labels 1 to 4 represent the upper right and lower left four directions respectively, and the second dimension corner labels 1 to 25 represent each point of the map, one time from the top left to the bottom right of the map is 1 to 25. Each value in the array, such as M[20][1]=15, indicates that the top of the point with map number 20 is the point with number 15, and M[20][2]=0 indicates that there is no path to the right of the point with map number 20. Where M[i][0]=0,M[0][j]=0)
Initialization: Define stack Q = {1} and set H = {}. (Q records all points in the current path in turn, H records all historical paths.)
Repeat the following actions until Q = {}:
_According to the top element D of Q stack and the adjacent table M, find all the adjacent point elements of d, and randomly select one element from it, and there is no such element in Q. If found, put the element into Q. If it cannot be found, the copy of Q is stored in H and D pops up from Q.
Output: H.
5. Algorithmic Implementation
So far, the abstract thinking process of the original problem and the theoretical analysis process of the algorithm have been described. The following is to use the actual code to implement the algorithm and achieve visualization. If visualization is not considered, any programming language can easily implement it. I wrote it in java before and output the results to the console. But it's not interesting. I want to visualize it. I didn't know how to visualize it for a long time, until I met React. After a thorough understanding, I found that using React to complete the visualization of the algorithm is really appropriate.
Because React is a component-oriented development model and can easily automatically render pages according to the state, the design of the visualization part becomes the disassembly of the original "map" and the definition of the state. The most basic components and overall styles I designed are as follows:
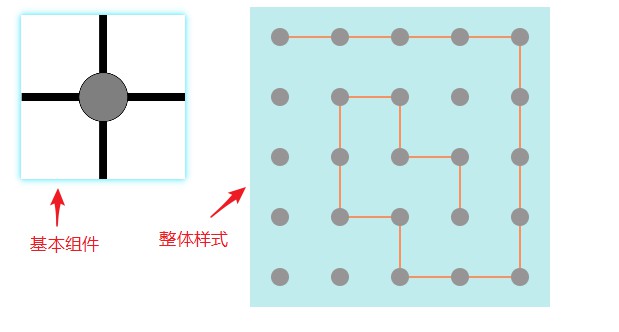
Each location (point) has four directions, from top to bottom, from top to bottom. If there is a connection between points, the lines in corresponding directions will be rendered as "block" by CSS and "none" by other rendering. This process will automatically render the interface according to the data status after defining the CSS style, without requiring repeated js writing. Rendering logic.
Ultimately, click on this Program Link 1 or Program Link 2 See. Some code is attached below. In addition, I have made some efforts to optimize the performance in the process of implementation, and will continue to optimize it in the future. Welcome interested friends to put forward their views.
import React, { Component } from 'react';
import './AppDemo.css';
import Grid from './Grid';
class AppDemo extends Component {
constructor(proprs) {
super(proprs);
var width = 5;
var height = 5;
var matrix = this.init(width,height);
var x = 50;
var start = Math.floor(Math.random() * width * height + 1);
this.state = {
matrix: matrix,
start: start,
arr: [start],
historyPath: [],
width: width,
height: height,
timeID: 0,
speed: 5,
random: true,
x: x,
time: 0
}
}
init(width,height){
var matrix = [[0, 1, 2, 3, 4]];
for (var numb = 1; numb <= width * height; numb++) {
var up = numb > width ? numb - width : 0;
var right = (numb % width) !== 0 ? numb + 1 : 0;
var down = numb <= width * (height - 1) ? numb + width : 0;
var left = ((numb - 1) % width) !== 0 ? numb - 1 : 0;
var arr = [numb];
arr.push(up);
arr.push(right);
arr.push(down);
arr.push(left);
matrix.push(arr);
}
return matrix;
}
handle() {
//var beginTime1=0;
//var beginTime2=0;
//beginTime1 = new Date().getTime();
var nowRow = this.state.arr[this.state.arr.length - 1];//Get the current location number
var arr = this.state.arr;//Path Number
var matrix = this.state.matrix;//Matrix storage structure
var historyPath = this.state.historyPath;//Historical Path
if (arr.length > 0) {//If path length > 0
var next = false;//Path not found by default
var ran = 1
if (this.state.random) {
ran = Math.floor(Math.random() * 4 + 1);
}
//var beginTime4 = new Date().getTime();
for (var i = 0; i < 4; i++) {
var nextNumb = matrix[nowRow][ran];
if (nextNumb !== 0 && !this.containNowPath(nextNumb)) {//Find the Path
arr.push(nextNumb);//Stack new elements
if (!this.containHistoryPath(arr)) {//If the new path does not appear in the historical path, then follow the path.
this.setState({
arr: arr
});
next = true;
break;
} else {//If a new path appears in a historical path, it is skipped.
arr.pop();//Abandon the position
ran = ran + 1 > 4 ? 1 : ran + 1;
}
} else {
ran = ran + 1 > 4 ? 1 : ran + 1;
}
}
//var beginTime5 = new Date().getTime();
if (!next) {//If there is no way to go
//Determine whether the current path (before retrogression) is included in the history.
if (!this.containHistoryPath(arr)) {
historyPath.push(arr.slice());//If it is not included in history, the new trial path is saved into the historical path set.
}
arr.pop();//To pop up the last element is a step backwards.
this.setState({//Modify the current changed state
arr: arr,
historyPath: historyPath
});
}
} else {//If the path traversal ends, the traversal continues at a different starting point.
this.stop();
// this.setState({
// start: this.state.start + 1,
// arr: [this.state.start + 1],
// historyPath: [],
// len: 5
// });
}
// beginTime2 = new Date().getTime();
// var time = beginTime2 - beginTime1 ;
// if(time> this.state.time){
// this.setState({// Modify the currently changed state
// time: time
// });
// }
//alert(time);
}
containNowPath(row) {//Determine whether the next location already exists in the current path.
var r = false;
for (var i = 0; i < this.state.arr.length; i++) {
r = this.state.arr[i] === row;
if (r) {
break;
}
}
return r;
}
containHistoryPath(arr) {//Find out from the historical path whether there is a path to follow
var r = false;
var historyPath = this.state.historyPath;
for (var i = historyPath.length - 1; i >= 0; i--) {
r = historyPath[i].toString().indexOf(arr.toString()) !== -1;
if (r) {
break;
}
}
return r;
}
render() {
return (
<div>
<div style={{ margin: "50px auto 0px auto", width: (this.state.width * this.state.x) + "px", minWidth: "700px" }}>
<div className="control">
<button type="button" onClick={() => this.start()}>start</button>
<button type="button" onClick={() => this.stop()}>suspend</button>
<button type="button" onClick={() => this.start()}>Continue</button>
<button type="button" onClick={() => this.step()}>One-step</button>
<apan style={{ margin: "0px auto 0px 10px", width: "120px", display: "inline-block" }}>Number of attempts:{this.state.historyPath.length}</apan>
<apan style={{ margin: "0px auto 0px 10px" }}>Speed:</apan>
<button style={this.state.speed === 1000 ? { backgroundColor: "#61dafb "}: {} type =" button "onClick = {() = > this. speed (1000)} > extremely slow </button>
<button style={this.state.speed === 500 ? { backgroundColor: "#61dafb "}: {} type =" button "onClick = {() = > this. speed (500)} > slow </button >
<button style={this.state.speed === 100 ? { backgroundColor: "#61dafb "}: {} type =" button "onClick = {() = > this. speed (100)}> in </button>
<button style={this.state.speed === 50 ? { backgroundColor: "#61dafb "}: {} type =" button "onClick = {() = > this. speed (50)} > fast </button>
<button style={this.state.speed === 5 ? { backgroundColor: "#61dafb "}: {} type =" button "onClick = {() = > this. speed (5)} > very fast </button>
<apan style={{ margin: "0px auto 0px 10px", width: "50px", display: "inline-block" }}></apan>
<button style={this.state.random ? { backgroundColor: "#61dafb "}: {} type =" button "onClick = {() = > this. random ()} > Random < / button > < br /> button
</div>
<div className="control2">
<button style={{ width: "80px" }} type="button" onClick={() => this.addheight(1)}>Additional rows+</button>
<button style={{ width: "80px" }} type="button" onClick={() => this.addwidth(1)}>Additional columns+</button>
<button style={{ width: "80px" }} type="button" onClick={() => this.big(1)}>enlarge+</button><br />
<button style={{ width: "80px" }} type="button" onClick={() => this.addheight(-1)}>Reduce rows-</button>
<button style={{ width: "80px" }} type="button" onClick={() => this.addwidth(-1)}>Reduced column-</button>
<button style={{ width: "80px" }} type="button" onClick={() => this.big(-1)}>narrow-</button>
</div>
<Grid x={this.state.x} width={this.state.width} height={this.state.height} arr={this.state.arr} />
</div>
</div >
)
}
addwidth(n) {
this.stop();
var width = this.state.width;
width = width + n;
if (width > 0 && width * this.state.x <= 1000) {
var matrix = this.init(width,this.state.height);
var start = Math.floor(Math.random() * width * this.state.height + 1);
this.setState({
matrix : matrix,
start: start,
arr: [start],
historyPath: [],
width: width
});
} else {
this.setState({
width: Math.floor(1000 / this.state.x),
});
}
}
addheight(n) {
this.stop();
var height = this.state.height;
height = height + n;
if (height > 0 && height * this.state.x <= 500) {
var matrix = this.init(this.state.width,height);
var start = Math.floor(Math.random() * this.state.width * height + 1);
this.setState({
matrix:matrix,
start: start,
arr: [start],
historyPath: [],
height: height
});
} else {
this.setState({
height: Math.floor(500 / this.state.x),
});
}
}
big(n) {
var x = this.state.x;
x = x + n;
if (x > 0 && ((x * this.state.width <= 1000) || (x*this.state.height<=500)) ){
this.setState({
x: x
});
} else {
this.setState({
x: Math.floor(x * this.state.width > x*this.state.height?1000/this.state.width:500/this.state.height)
});
}
}
// shouldComponentUpdate(nextProps, nextState){
// return nextState.arr.length>100;
// }
step() {
this.stop();
this.handle();
}
start() {
var timeID = this.state.timeID;
if (timeID === 0) {
timeID = setInterval(
() => this.handle(),
this.state.speed
);
}
this.setState({
timeID: timeID
});
}
stop() {
var timeID = this.state.timeID;
if (timeID !== 0) {
clearInterval(timeID);
}
this.setState({
timeID: 0
});
}
componentDidMount() {
var matrix = [[0, 1, 2, 3, 4]];
var width = this.state.width;
var height = this.state.height;
for (var numb = 1; numb <= width * height; numb++) {
var up = numb > width ? numb - width : 0;
var right = (numb % width) !== 0 ? numb + 1 : 0;
var down = numb <= width * (height - 1) ? numb + width : 0;
var left = ((numb - 1) % width) !== 0 ? numb - 1 : 0;
var arr = [numb];
arr.push(up);
arr.push(right);
arr.push(down);
arr.push(left);
matrix.push(arr);
}
}
speed(n) {
var timeID = this.state.timeID;
clearInterval(timeID);
timeID = 0;
timeID = setInterval(
() => this.handle(),
n
);
this.setState({
timeID: timeID,
speed: n
});
}
random() {
this.setState({
random: !this.state.random
});
}
sleep(numberMillis) {
var now = new Date();
var exitTime = now.getTime() + numberMillis;
while (true) {
now = new Date();
if (now.getTime() > exitTime)
return true;
}
}
}
export default AppDemo;