The two key points in studying Fairplay DRM (Digital Rights Management) are authorization and encryption. However, there has been little research on App DRM for a long time, and it is on this premise that Fairplay DRM has superimposed a "barrier" for the security research of iOS App. By analyzing the problems in the design and implementation of the confusion system, we overcome the obstacles of debugging and tracking, and designed a variety of static and dynamic countermeasures; At the same time, through a large number of reverse engineering, it fills the cognitive gap of security researchers on Fairplay in macOS system mechanism.
What is DRM?
The full name of DRM is Digital Rights Management, that is, digital copyright protection. In order to protect the music / videos / books / apps distributed in the App Store from piracy, Apple has developed Fairplay DRM Technology and applied for many relevant patents, such as:
- US8934624B2: Decoupling rights in a digital content unit from download
- US8165286B2: Combination white box/black box cryptographic processes and apparatus
- ES2373131T3: Safe distribution of content using descifrado keys
For a long time, there has been little research on App DRM, and the key of DRM is authorization and encryption. The way to crack Fairplay DRM encryption is commonly known as "smashing the shell", which is a necessary prerequisite for iOS App security research. Since Apple introduced the App DRM mechanism in 2013, classic "shell smashing tools" such as clutch, Bagbak and Flexdecrypt have been born. Such "shell smashing tools" usually need the support of jailbreak devices, so they have certain limitations.
M1 Mac released in 2020 introduces Fairplay DRM mechanism into MacOS. Since the permissions of Mac devices are not as strict as iOS, we can explore more principles of Fairplay DRM on MacOS, and the ultimate goal is to make the decryption process not limited by Apple platform. Next, let's talk about how it is implemented in apple?
Implementation of DRM on Apple: Fairplay DRM
LC_ ENCRYPTION_ Tags in info
Encrypted MachO contains LC_ENCRYPTION_INFO field, where cryptoff identifies the starting offset of the encrypted part in the file, cryptsize identifies the size of the encrypted part, and cryptid indicates the encryption method. The encryption size of the App under Fairplay DRM protection is a multiple of 4096, and the encryption method id is 1.
The components responsible for decrypting Mach-O mainly include FairplayIOKit in kernel state and fairplayd in user state.
Fairplay's Open
Text in XNU Kernel of MacOS_ crypter_ create_ Hook is the export symbol, and the IOTextEncryptionFamily driver registers the hook and forwards the call to the FairplayIOKit kernel driver as a bridge.

The final function responsible for processing is:
com_apple_driver_FairPlayIOKit::xhU6d1( char const* executable_path, long long cpu_type, long long cpu_subtype, rp6S0jzg** out_handle )
After that, FairplayIOKit in the kernel starts to initialize through host_ get_ special_ Unfree port in port sends MIG call to fairplay in user status, and fairplay starts processing SC_ The sinf and sup files in the info directory and return the processed data to the FairplayIOKit in the kernel.
Note: the specific workflow of fairplay in user status is beyond the scope of this article.
The structure of MIG call is as follows:
struct FPRequest{
mach_msg_header_t header;
mach_msg_body_t body;
mach_msg_ool_descriptor_t ool;
NDR_record_t ndr;
uint32_t size;
uint64_t cpu_type;
uint64_t cpu_subtype;
};
struct FPResponse{
mach_msg_header_t header;
mach_msg_body_t body;
mach_msg_ool_descriptor_t ool1; //supf file mapping
mach_msg_ool_descriptor_t ool2; //unk, proportional to the size of the encrypted content
uint64_t unk1;
uint8_t unk2[136];
uint8_t unk3[84];
uint32_t size1;
uint32_t size2;
uint64_t unk5;
};After all the calls are completed, the returned structure rp6S0jzg * is actually a uint32_t-type handle, and then you can use this handle to complete the decryption operation.
Decrypt Page of Fairplay
The Fairplay Open operation mentioned earlier finally returns a pager_crypt_info structure, where page_ The decrypt Hook is taken over by the IOTextEncryptionFamily driver and finally forwarded to FairplayIOKit.

Finally, the decryption function in FairplayIOKit is defined as follows:
com_apple_driver_FairPlayIOKit::bvqhJ( rp6S0jzg *hanlde, unsigned long long offset, unsigned char const* src, unsigned char * dst )
At this point, Fairplay's decryption logic completes the call. It is worth noting that in Fairplay DRM, the concept of page is 4096 bytes.
So what are the sinf and sup files processed by fairplay in user mode?
SINF and SUPF files
structure
Fairplay in user mode will read two important files carried with IPA: SINF and SUPF, which are stored in the SC of App_ Info directory.
The SUPF file and IPA are distributed together, and the IPA and SUPF files of each user are consistent. The key for encrypting Mach-O is saved in the SUPF file, but the key itself is encrypted by another mechanism. As the DRM license of each user, the SINF file records the identifier and name of the purchased user and the information required to decrypt SUPF. Therefore, under the Sandbox policy, App cannot read its own SINF file to prevent it from tracking users as a unique ID.
SINF
SINF file is a file with LTV+KV structure, and its fields are as follows:
sinf.frma: game sinf.schm: itun sinf.schi.user: 0xdeadbeef sinf.schi.key : 0x00000005 sinf.schi.iviv: 0x12345678901234567890123456789012 sinf.schi.righ.veID: 0x000007d3 sinf.schi.righ.plat: 0x00000000 sinf.schi.righ.aver: 0x01010100 sinf.schi.righ.tran: 0xdc64f80c sinf.schi.righ.sing: 0x00000000 sinf.schi.righ.song: 0x59a73c58 sinf.schi.righ.tool: P550 sinf.schi.righ.medi: 0x00000080 sinf.schi.righ.mode: 0x00002000 sinf.schi.righ.hi32: 0x00000004 sinf.schi.name: User Name sinf.schi.priv: (432 Bytes Private Key) sinf.sign: (128 Bytes Private)
SUPF
The SUPF file is mainly divided into three parts. We name them Key Segments, Fairplay Certificate and RSA Signature. Key Segments can contain multiple sub segments to save the decryption information of multiple architectures.
KeyPair Segments:
Segment 0x0: arm64, Keys: 0x36c/4k, sha1sum = e369546960d805dd1188d42e3350430c7e3a0025
Fairplay Certificate:
Data:
Version: 3 (0x2)
Serial Number:
33:33:af:08:07:08:af:00:01:af:00:00:10
Signature Algorithm: sha1WithRSAEncryption
Issuer: C=US, O=Apple Inc., OU=Apple Certification Authority, CN=Apple FairPlay Certification Authority
Validity
Not Before: Jul 8 00:48:29 2008 GMT
Not After : Jul 7 00:48:29 2013 GMT
Subject: C=US, O=Apple Inc., OU=Apple FairPlay, CN=AP.3333AF080708AF0001AF000010
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
RSA Public-Key: (1024 bit)
Modulus:
00:b0:01:16:4b:62:b2:37:8d:60:12:4f:02:15:15:
a0:32:1b:e8:ed:44:ed:e9:17:5b:ec:9e:5d:11:24:
5a:66:2f:dc:a3:25:aa:52:70:e1:09:22:09:4b:65:
0f:67:f5:82:dc:af:78:9b:4c:45:f3:b4:f4:77:aa:
fc:a3:b2:84:c3:8b:09:c6:2e:55:f5:14:85:07:ac:
ae:0d:ff:ff:ca:41:3b:44:cb:52:b6:28:60:55:23:
35:8d:26:71:c6:12:a5:e0:72:58:09:3c:4a:9e:b6:
63:df:2a:91:94:27:eb:65:0a:b2:36:45:11:c1:91:
43:58:12:d9:e5:18:a1:ad:db
Exponent: 65537 (0x10001)
X509v3 extensions:
X509v3 Key Usage: critical
Digital Signature, Key Encipherment, Data Encipherment, Key Agreement
X509v3 Basic Constraints: critical
CA:FALSE
X509v3 Subject Key Identifier:
7B:07:34:81:A5:75:D0:F6:11:BB:D2:36:3F:79:93:4B:A1:70:EB:CF
X509v3 Authority Key Identifier:
keyid:FA:0D:D4:11:91:1B:E6:B2:4E:1E:06:49:94:11:DD:63:62:07:59:64
Signature Algorithm: sha1WithRSAEncryption
06:11:4e:87:ed:b1:08:70:c2:0d:e4:d2:94:bb:7f:ee:50:18:
c0:2a:21:34:0e:99:1f:bf:60:a2:58:d0:0c:28:3d:03:5b:ab:
4e:72:69:ba:41:52:45:b2:29:27:4a:c8:ba:7f:b5:9b:63:78:
b1:68:41:40:59:3f:05:8a:57:74:c5:63:30:cc:f3:20:41:c0:
3c:65:d4:0d:22:47:f3:97:76:e6:d6:3c:eb:e7:20:78:10:59:
fd:96:09:82:c3:41:f0:5f:d0:3e:91:44:6d:77:3f:a5:d9:da:
f0:f7:53:ad:94:61:28:1c:4c:40:3b:17:2b:dd:e3:00:df:77:
71:22
RSA Signature: 6aeb00124d62f75f5761f7c26ec866a061f0776be7e84bfad4b6a1941dbddfdb3bd1afdcc5ef305877fa5bee41caa37b1a9d4ce763cf7d2cb89efa60660a49dd5ddff0f46eee7cd916d382f727d912e82b6e0a62e8110c195e298481aa8c8162faac066ef017c6c2c508700d7adb57e0c988af437621e698946da1b09adf89e9Next, let's talk about the confusion principle and implementation of Fairplay DRM.
Confusion principle and some implementations
LLVM Pass
LLVM is an excellent compiler framework, which can be roughly divided into front end, middle end and back end:
The drawing is excerpted from CS 15-745 course of CMU: https://www.cs.cmu.edu/~15745.
The front end is responsible for converting the high-level language into LLVM IR; The middle end processes LLVM IR, completes a series of analysis and optimization tasks, which we call Pass, and outputs LLVM IR again; The back end is responsible for converting LLVM IR into machine code. Among them, the middle end has rich playing methods, and the basic optimization tasks such as dead code elimination and constant folding are completed in this part; Address Sanitizer, PC Sanitizer and other compiler instrumentation are also carried out here; Other confusion frameworks, such as the more discussed ollvm and Hikari, and even Apple's confusion mechanism, are also based on this.
This confusion can be basically divided into control flow confusion and data flow confusion. In addition, some confusion methods, such as VMP, are not discussed in this paper.
makeOpaque
In the compiler, in order to prevent some specific expressions from being optimized, we will make equivalent changes to the expressions. We temporarily define such operations as makeOpaque (such as Safari's JavaScript core, whose JIT component B3 provides such a mechanism). The C + + pseudo code is as follows:
Expression* makeOpaque(Expression *in);
Opaque Predicate
A Predicate in a computer refers to an expression that is True or False after execution. Some conclusions in number theory can be used as the basis for generating opaque predicates. The results of these opaque predicates are always True or False. For example, in the following expression, the result of y execution is always True:
uint32_t x = 0; bool y = ((x * x % 4) == 0 || (x * x % 4) == 1);
An example of opaque predicates applied to obfuscation is bogus CFG.
The source statement is as follows:
foo1(); foo2();
After transformation, we added a false branch (i.e. bogus CFG)
:
foo1(); if ( false ) junk_code(); else foo2();
However, if there is no special treatment, the dead code elimination of the compiler and decompiler will remove the false branches. Therefore, we need to introduce makeOpaque. Suppose we introduce the expression in the previous example:
foo1(); uint32_t x = rand(); bool y = ((x * x % 4) == 0 || (x * x % 4) == 1); if ( !y ) junk_code(); else foo2();
If the compiler and decompiler have no corresponding recognition mechanism, this part of the dead code will be retained. Inserting a large number of interference instructions into the dead code can bring great trouble to the reverse personnel. After testing, Clang 11 can recognize this rule under - O2 optimization, but GCC 5.4 cannot.
Reversible transformation
Here we introduce the equivalent transformation methods commonly used in confusion technology.
XOR
XOR rule is the most common transformation, which will not be repeated here.
x ^ c ^ c = x;
Affine transformation
Let's first look at affine functions.

Let's take a look at the practical application.
Because the operation in the computer belongs to implicit modular operation, it will have some interesting properties. For example, for an operation on uint32, the inverse element of modular operation is defined as follows:
//about uint32_t a, r_a; //If satisfied (a * r_a) % UINT32_MAX == 1; //So a and r_a are reciprocal modular elements
For a and R which are reciprocal modular elements_ A (which can be obtained by extended Euclidean algorithm) has the following characteristics:
uint32_t x = rand(); uint32_t y1 = a * x + c; //So satisfied x == ra * y1 + (- ra * c)
Finally, an example is given to illustrate:
//For 4872655123 * 3980501275 which are reciprocal elements, take uint32_t x = 0xdeadbeef; uint32_t c = 0xbeefbeef; //Then - ra * c = 0x57f38dcb, and ((x * 4872655123) + 0xbeefbeef) * 3980501275 + 0x57f38dcb == x /* The following can be verified in lldb (lldb) p/x uint32_t x=0xdeadbeef; (uint32_t)(((x * 4872655123) + 0xbeefbeef) * 3980501275 + 0x57f38dcb) (uint32_t) $8 = 0xdeadbeef */
MBA expression (mixed Boolean arithmetic expression)
MBA expression is a confusing method to hide the original expression by mixing arithmetic operations (+,, *, /) and bit operations (&, |, ~). It has many forms based on different mathematical principles. Here we mainly introduce polynomial MBA, which is the most common form in confusion technology.

Similarly, the MBA expression used in Fairplay confusion is:
//OperationSet(+, -, *, &, |, ~) x - c = (x ^ ~c) + ((2 * x) & ~(2 * c + 1)) + 1;
The confusion operation using MBA mainly depends on the following two steps:

Opaque Constant
Opaque constant is a method based on MBA confusion, which is used to hide constants in data flow. It uses permutation polynomials, which are reversible polynomials over finite fields.

Control flow flattening
This part is the hottest topic discussed in reverse engineering, that is, the normal control flow conversion is equivalent to a state machine, which interferes with the static control flow analysis. There are many solutions in the industry. At the same time, because this type of confusion is not obviously used in Fairplay DRM, it will not be discussed more.
Indirect Branch
The starting addresses of some basic blocks are saved in global variables. Through the generation of opaque constants, the disassembly tool and the naked eye cannot directly obtain the target of basic block jump. The model is as follows:
//Record the basic block address to the global lookup table LUT LUT[i] = PC; //Perform jump jmp/call LUT[makeOpaque(i)]
Specific examples:

In this way, the reverse engineer cannot directly obtain the jump objective function and basic block. Similarly, by mapping the conditions of the judgment statement to the jump table, the confusion of conditional jump can also be realized.
Therefore, when reversing the confused Fairplay code, IDA Pro can only recognize the first basic block of the function most of the time, and cannot analyze the boundary of the function.
Cross function confusion + call convention confusion
Under normal circumstances, the parameter transfer of programming languages such as C language follows specific calling conventions, but some confusion tools will modify the calling conventions of some internal functions. Take Fairplay DRM as an example:
We can see that the conventional method of transferring parameters by register and stack is replaced by the method of transferring parameters by heap. When the structure is constructed, the characteristics of parameter transfer can be clearly seen. At the same time, some parameters passed here are XOR confused and restored in the sub function, which makes it difficult for us to directly obtain the original data, and static analysis tools such as IDA Pro do not support cross function data flow analysis.
More seriously, some important dependent data affecting the operation of child functions are promoted to the parent function, so we can't infer the operation process of child functions until the call relationship is restored.
Then, the way to crack Fairplay DRM is to find its weaknesses.
Fairplay confusion weakness
Through the previous work, we have been able to open and decrypt Fairplay normally. Through a series of static analysis and tracking debugging, we have found some countermeasures for this confusing system.
The essential reason for these problems is that the confusion system is designed at the IR level and does not confuse some machine related operations. Therefore, in the generated machine code, we can infer some characteristic information before confusion.
Function boundary identification
As mentioned earlier, due to the confusion technology of indirect jump used in Fairplay, IDA Pro cannot directly analyze the boundary of the function. Through tracking, we found that under the arm64e device, all basic blocks of the same function in the kernel driver use the same PAC Context, or PAC Modifier, when running to the jump instruction.
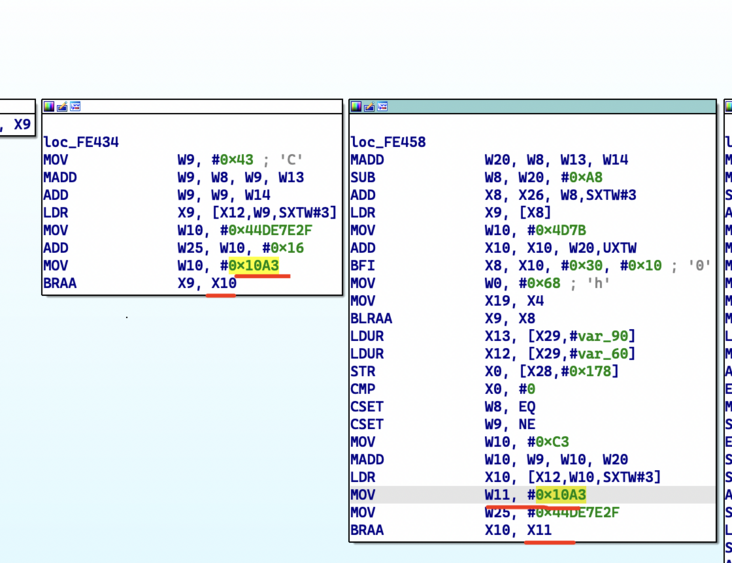
With this feature, we can group the boundaries of functions and basic blocks, although these basic blocks are not connected so far.
Indirect jump
For unconditional jump, we can solve it by setting breakpoints to track the execution flow.
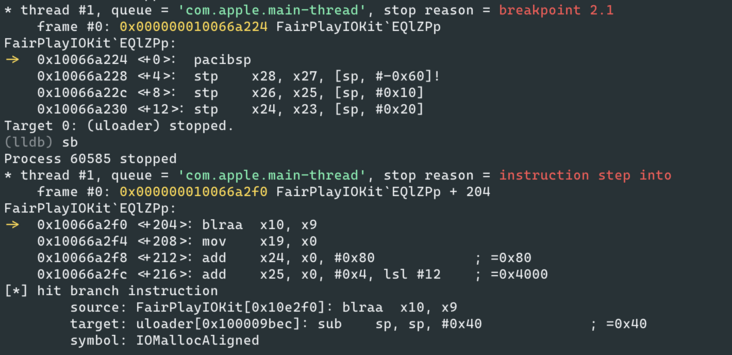
Through tools such as KeyPatch, we can restore some simple functions to a point that is easy to understand.
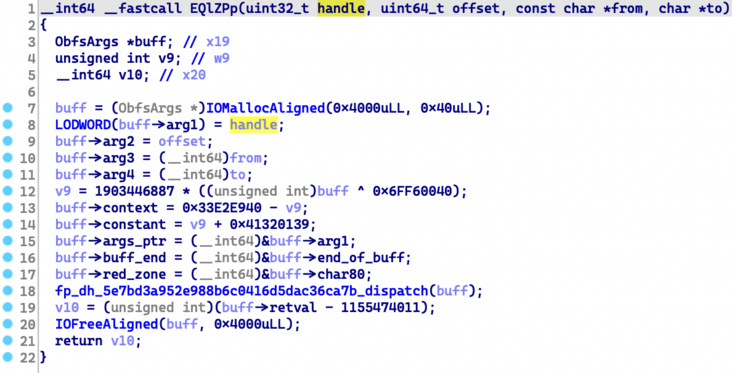
However, the difficulty here is to recover the indirect jump instruction in the confusion, as shown in the figure below:
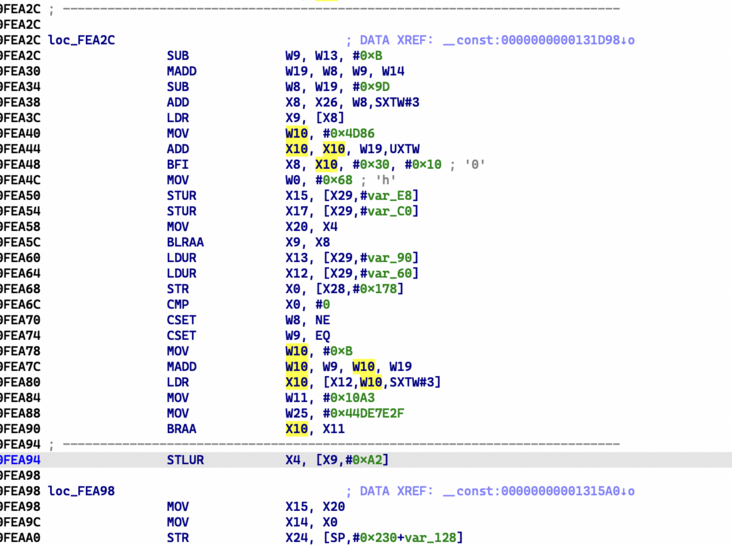
For this jump instruction, we can generate the following expression:
//cmp x0, #0 w10 = qword[x12 + (EQ * 0xB + w19) << 3] //0xB represents the subscript difference of two basic blocks in LUT
Through the form of CSET instruction, we can infer that the jump instruction should be J.NE or J.EQ. through our debugger plug-in, we can get the jump address of one branch and the original jump instruction, and then we can quickly infer the address of another branch through the expression information.
Through Keypatch, we can get the branch statement structure before confusion:
At this point, we can completely restore most of the control flow of Fairplay.
Data stream confusion
We have mentioned some in this part. At present, we have found the pattern of MBA expression, but we have not found the complete rule for generating opaque constants in Fairplay. There seems to be only one rewriting rule for MBA expression, that is:
x - c = (x ^ ~c) + ((2 * x) & ~(2 * c + 1)) + 1;
Some tools based on pattern matching, such as D810, can handle this situation better.
Conclusion
At present, we can obtain the AES key for decrypting each Mach-O section. Through a lot of debugging and anti confusion, we have come to the preliminary conclusion of the generation of these keys. We hope that the ultimate goal is to complete the research on Fairplay DRM encryption and decryption without relying on Apple devices.
Finally, attached Source code , you are welcome to make reference and research.
reference
- Eyrolles, N. (2017). Obfuscation with Mixed Boolean-Arithmetic Expressions: reconstruction, analysis and simplification tools (Doctoral dissertation, Université Paris-Saclay)
- https://github.com/obfuscator-llvm/obfuscator
- https://github.com/HikariObfuscator/Hikari
- https://github.com/keystone-engine/keypatch
- https://eshard.com/posts/d810_blog_post_1
Introduction to the author
Wu Liao, Luo Luo and Zhu MI are all from the information security department of meituan.
Read the collection of more technical articles of meituan technical team
front end | algorithm | back-end | data | security | Operation and maintenance | iOS | Android | test
Special purchases for the Spring Festival official account, special purchases for the Spring Festival, special purchases for the Spring Festival, special purchases for the Spring Festival, etc., in the public menu bar dialog box, to reply to the following 2020 items: the 2019 year goods, the 2018 goods and the 2017 goods.

|This article is produced by meituan's technical team, and the copyright belongs to meituan. You are welcome to reprint or use the content of this article for non-commercial purposes such as sharing and communication. Please indicate that "the content is reprinted from meituan technical team". This article may not be reproduced or used commercially without permission. For any business activities, please send an email to tech@meituan.com Apply for authorization.