Author: Grey

Original address: Redis learning notes 7: master-slave replication and sentinel

What are the problems with single machine, single node and single instance Redis?

It is easy to cause single point of failure, so how to solve it?

Active / standby mode

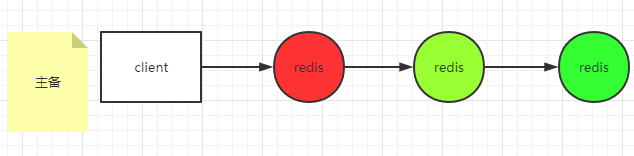
At the same time, read-write separation can be realized

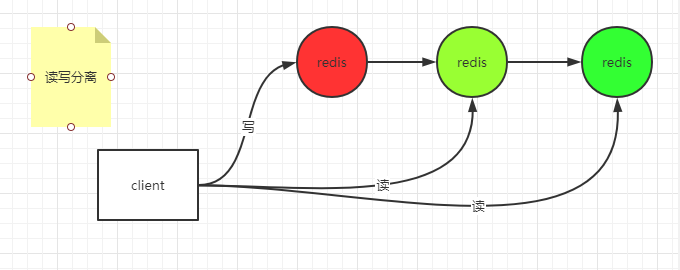
Each node here is full and mirrored.

The capacity of a single node is limited and the pressure at a single point is relatively large. How to solve it?

Different business data can be stored in different instances

Each business data can also be put into the same group of Redis databases according to different rules

After introducing multiple Redis instances, there will be data consistency problems. How to solve them?

If you want to achieve strong consistency (synchronization mode), it will easily lead to unavailability. For example, after a node is successfully written, it will synchronize to other nodes. Assuming that other nodes have a network delay or failure, the whole service will be unavailable. Therefore, if you want to ensure availability, you need to tolerate the loss of some data (if the primary node writes successfully, it immediately returns success to the client, and asynchronously synchronizes the data to other standby nodes). If you want to ensure no data loss (final consistency), you can consider using message queue.

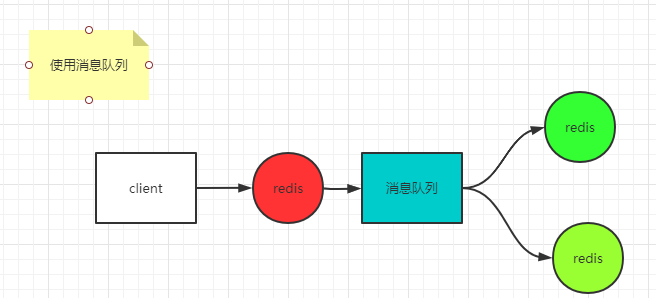
Here, the message queue itself is required to be reliable. This method ensures the final consistency, and there will be problems. For example, when multiple clients access, inconsistent data may be obtained.

Master-slave mode

The client can access the master or slave

Active standby mode

The client only accesses the primary server, not the standby server. The client only accesses the standby server when the primary server hangs up

Both master-slave and master-slave become single point of failure. How to solve this problem?

Therefore, HA must be done for the host (for example, when the host hangs up, it can be used as the host from the top)
To HA the master, you must select a highly available monitor,
The design of monitoring programs should be considered. It is only when multiple monitoring programs report that Redis is hung that Redis is really hung (otherwise, it is easy to cause brain crack, that is, data partition)

If there are n nodes, N/2+1 nodes need to report exceptions (more than half) to be considered as true exceptions.

Whether brain fissure should be handled depends on your regional tolerance.

It is better to have an odd number of machines.

Master-slave replication experiment

Install three redis instances on one machine through the install_server.sh script

• 6379

• 6380

• 6381

First, stop the three instances, and then put the configuration files of the three instances in one place. I put them in the / data directory

cp /etc/redic/*.conf /data/

Modify the following configuration for the three instances

# Close aof
appendonly no

# Set foreground operation
daemonize no

# Comment out logfile
# logfile /var/log/redis_6379.log

Then start three instances

redis-server /data/6379.conf
redis-server /data/6380.conf
redis-server /data/6381.conf

Start client

redis-cli -p 6379
redis-cli -p 6380
redis-cli -p 6381

Set 6380 and 6381 as the slave of 6379 and execute on both 6380 and 6381 clients

replicaof 127.0.0.1 6379

We execute a statement on the 6379 client

set k1 from6379

Then perform at both 6380 and 6381

127.0.0.1:6381> get k1
"from6379"

127.0.0.1:6380> get k1
"from6379"

You can see the data synchronized from the slave to the host

The client of any one of 6380 or 6381 executes

127.0.0.1:6381> set k2 asdfasd
(error) READONLY You can't write against a read only replica.

The following information will be prompted:

(error) READONLY You can't write against a read only replica.

That is, the slave cannot write.

Suppose that one of the two slaves is suspended, and after the suspension, the host also performs several operations. At this time, if the suspended slave continues to start (in the – appendonly no mode), only incremental data synchronization will be performed.
If the suspended slave is started in the appendonly yes mode, full synchronization will be triggered

rdb can record the original followers' information, so it can be incremental, while aof will not record, so it can only be full.

If the master hangs up, because the slave can only read and cannot write, we can artificially turn one of the slaves into the master (execute on this slave first: replicaof no one) Then let another slave follow the master. During the following process, if the slave turns on replica serve stale data = yes, the slave can also query its own old data when synchronizing the host data,

Replica diskless sync yes means that the network is used directly to synchronize the data of the master and slave (without falling on the disk). This situation is generally applicable to the case where the disk performance is lower than the network performance.

repl—backlog-size 1mb
The queue size maintained by the host to prevent the slave from hanging up after restarting. This maintains an offset. If the write frequency is not high, it can be set to 1mb. If the write frequency is very high, this value should be appropriately increased.

# Specify the minimum number of successful writes
min-replicas-to-write 3
min-replicas-max-lag 10

Problems with master-slave replication:

Therefore, it is necessary to manually maintain the main fault!

So ha is needed. How does ha do it?

Introduction: sentinel mechanism

sentinel experiment

Keep the three previously configured hosts (one master and two slaves) in the startup state
Among them, 6379 is the main, 6380 and 6381 are the secondary.

Prepare three sentinel configuration files (configured to monitor the host)

Prepare three configuration files: 26380.conf, 26381.conf and 26379.conf in the / data/redis/sentinel directory. The following contents are configured in the configuration file. Take 26379.conf as an example (the other two are the same)

port 26379
sentinel monitor mymaster 127.0.0.1 6379 2

For configuration description, see: http://www.redis.cn/topics/sentinel.html

After the three configurations are ready, we start the three instances in sentinel mode. The startup commands are as follows: take 26379 as an example, and the other two are the same.

redis-server /data/redis/sentinel/26381.conf --sentinel

After startup, we simulate the host to hang up and stop the 6379 instance,

service redis_6379 stop

Check the log of any sentinel instance, find that a new epoch is opened, and select the new master as 6380

4594:X 29 May 2021 16:32:19.997 # +new-epoch 1
4594:X 29 May 2021 16:32:19.999 # +vote-for-leader 27e706bf27e99c10310c6c9595fcffef63d67e60 1
4594:X 29 May 2021 16:32:20.762 # +config-update-from sentinel 27e706bf27e99c10310c6c9595fcffef63d67e60 127.0.0.1 26380 @ mymaster 127.0.0.1 6379
4594:X 29 May 2021 16:32:20.762 # +switch-master mymaster 127.0.0.1 6379 127.0.0.1 6380
4594:X 29 May 2021 16:32:20.762 * +slave slave 127.0.0.1:6381 127.0.0.1 6381 @ mymaster 127.0.0.1 6380
4594:X 29 May 2021 16:32:20.762 * +slave slave 127.0.0.1:6379 127.0.0.1 6379 @ mymaster 127.0.0.1 6380

Connect 6380 with a client to perform set operation

[root@base ~]# redis-cli -p 6380
127.0.0.1:6380> set k1 ddd
OK

The operation is successful, then connect 6381 and try to get k1

[root@base ~]# redis-cli -p 6381
127.0.0.1:6381> get k1
"ddd"

After obtaining the latest data, restart the instance 6379, and then open the running log of any sentinel

4594:X 29 May 2021 16:32:50.823 # +sdown slave 127.0.0.1:6379 127.0.0.1 6379 @ mymaster 127.0.0.1 6380
4594:X 29 May 2021 16:36:16.528 # -sdown slave 127.0.0.1:6379 127.0.0.1 6379 @ mymaster 127.0.0.1 6380

It is found that 6379 has followed 6380 as a slave
Try to get and set values in 6379

[root@base ~]# redis-cli -p 6379
127.0.0.1:6379> get k1
"ddd"
127.0.0.1:6379> set k1 asdf
(error) READONLY You can't write against a read only replica.

You can get, but you can't set.

more

Since the host knows that it has several slaves, sentinel can also know how many slaves the host has as long as it monitors the host.
How does a sentinel know about other sentinels? It uses the publish and subscribe function in redis.