Recursive Implementation of Binary Tree

Recursive implementation of binary tree

In learning data structure, we have to mention the concept of tree. Usually, learning begins with simplicity, so we start with simplicity and realize a simple binary tree. And three kinds of traversal are realized respectively.

When it comes to binary trees, we need to understand the structure of binary trees first, and I won't say much about it. There are many nodes in a tree, and each node has its own value data, left subtree and right subtree. So we need to define the structure of a node and initialize it (through the initialization list):

template<class T>
struct BinaryTreeNode
{
	T _data;
	BinaryTreeNode<T>* _left;
	BinaryTreeNode<T>* _right;

	BinaryTreeNode(const T& x)
		: _data(x)
		, _left(NULL)
		, _right(NULL)
	{}
};

Recursive Implementation of Binary Tree

The binary tree is implemented recursively. Then we implement the basic member functions of a class recursively (1) constructor, 2 copy constructor, 3 assignment operator overloading (except) and 4 destructor).

For convenience of definition, the node is renamed Node.

Constructor:

BinaryTree(T* a, size_t size, const T& invalid = T())
	{
		assert(a);
		size_t index = 0;
		_root = _CreateTree(a, size, invalid, index);
	}

Node* _CreateTree(T* a, size_t size, const T& invalid, size_t& index)
	{
		if (index < size && a[index] != invalid)
		{
			Node* root = new Node(a[index]);
			root->_left = _CreateTree(a, size, invalid, ++index);
			root->_right = _CreateTree(a, size, invalid, ++index);
			return root;
		}
		return NULL;
	}

A tree, recursive implementation, we need to know how to achieve this tree. I won't explain much about the definition of binary tree, but you have to think about how recursion is implemented according to the structure of the tree. A binary tree, starting from the root node, will continue to go down, go to the left, it will go to the right, and what we need to do is to divide this into sub-problems to think about.

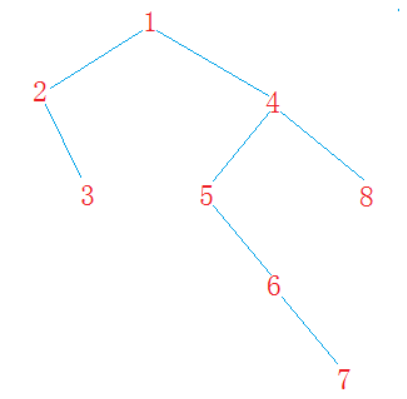
Take the simple binary tree above as an example. You go down from the root node 1 to the root node 2, then go down from the root node 2 to the root node 3, then go down without any nodes, then go back, then go back to the root node, go up in turn, go back to the root node 1, then go right, go 4, then go left, then go down 5 as the root node, and finally go to the root node. 7 returns, returns to 4, then goes to the right, goes back to the root node 1, and finally completes the recursion.

Of course, we have to interpret the code as well. First of all, we build trees through arrays, so the parameters will be passed an array and size. Of course, we need to know how to judge whether to reach the leaf node, right. So we set an unreasonable value to mark whether to reach the leaf node, and whether to recurse down.

Of course, you'll see a variable called index in the code. What's this for? In fact, it is used to mark the array, equivalent to the subscript of the array, so that we can easily use the array, of course, it is important to recursively use it you need to pass references, after all, it is constantly going online, you can not use it to reset, so you can not achieve the purpose of traversing the array.

(2) Copy constructor:

BinaryTree(const BinaryTree<T>& t)
	{
		_root = _Copy(t._root);
	}

Node* _Copy(Node* root)
	{
		if (root == NULL)
		{
			return NULL;
		}

		Node* NewNode = new Node(root->_data);
		NewNode->_left = _Copy(root->_left);
		NewNode->_right = _Copy(root->_right);

		return NewNode;
	}

In fact, after I explained the above recursive implementation method, it is easier for you to see the implementation method of this copy construction again. Open a new root node and recurse down until the empty root node returns. Otherwise, you will go down, either left or right, and finally play the whole binary tree, so that you can get the original. The binary tree is copied into a new binary tree.

(3) Overload of assignment operators:

BinaryTree<T>& operator=(BinaryTree<T> t)
	{
		std::swap(_root, t._root);
		return *this;
	}

This I will not explain more, call the exchange function in the library, directly exchange the original binary tree and the new one, so as to achieve the role of assignment.

(4) Destructive function:

	~BinaryTree()
	{
		_Destroy(_root);
	}

void _Destroy(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		if (root->_left != NULL)
		{
			_Destroy(root->_left);
			root->_left = NULL;
		}
		if (root->_right != NULL)
		{
			_Destroy(root->_right);
			root->_right = NULL;
		}

		delete root;
		root = NULL;
		return;
	}

As for the final destructor, we still use recursion. When the root node is empty, we return directly to empty. If it is not empty, then we recurse down to determine whether the left subtree is empty or not. If not, we continue to recurse down until the low-orbit leaf node, then delete is released and set to empty. Then we return up and finally release all the space in the tree. Let go.

Then several traversals will continue to be implemented recursively.

Recursive traversal of binary trees

In fact, the traversal of binary tree, several kinds of traversal recursive implementation are the same, here I will first traversal to do a simple explanation.

First traverse, first visit the root node, then access the left subtree, and then access the right subtree. Looking at the code, you will find that the code is simple, or in a recursive way. Every time you visit a node, you first access the data in the node, then access its left subtree and right subtree until you access the leaf node, then return up until you reach the root node, and then exit the recursion.

As for intermediate traversal and post-order traversal, you only need to understand the traversal mode of intermediate traversal and post-order traversal to write out.

(1) Preorder traversal:

void PrevOrder()
	{
		_PrevOrder(_root);
		cout << endl;
	}

void _PrevOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		cout << root->_data << " ";
		_PrevOrder(root->_left);
		_PrevOrder(root->_right);
	}

(2) Mid-order traversal:

void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

void _InOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		_InOrder(root->_left);
		cout << root->_data << " ";
		_InOrder(root->_right);
	}

(3) Postorder traversal:

void PostOrder()
	{
		_PostOrder(_root);
		cout << endl;
	}

void _PostOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		_PostOrder(root->_left);
		_PostOrder(root->_right);
		cout << root->_data << " ";
	}

Non-recursive traversal of binary trees

In fact, the way of non-recursive traversal is relatively simple, but without recursion, we need to use the stack to help us achieve, keep pressing the nodes on the stack, and then output the data before going out of the stack.

Or take the precedent traversal as an illustration, if the stack is not empty or the node is not empty, then print the data, and continue to go left down and press the node into the stack until the left child has all traversed, and then go back to the top, back to the last node and then go right, or as a sub-problem, the left traversal to the root node. Then go right, go out of the stack, then go right, go back to the last root node, then go out of the stack, repeat the process so that you can traverse all the nodes and achieve non-recursive traversal.

(1) Preorder traversal:

void PrevOrderNonR()
	{
		stack<Node*> s;
		Node* cur = _root;

		while (!s.empty() || cur)
		{
			while (cur)
			{
				cout << cur->_data << " ";
				s.push(cur);
				cur = cur->_left;
			}

			Node* top = s.top();
			cur = top->_right;
			s.pop();
		}
		cout << endl;
	}

(2) Mid-order traversal:

void InOrderNonR()
	{
		stack<Node*> s;
		Node* cur = _root;
		while (cur || !s.empty())
		{
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}

			Node* top = s.top();
			cout << top->_data << " ";
			cur = top->_right;

			s.pop();
		}
		cout << endl;
	}

(3) Postorder traversal:

void PostOrderNonR()
	{
		stack<Node*> s;
		Node* cur = _root;
		Node* prev = NULL;
		while (!s.empty() || cur)
		{
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}
			Node* top = s.top();
			if (top->_right==NULL || top->_right == prev)
			{
				cout << top->_data << " ";
				prev = top;
				s.pop();
			}
			else
			{
				cur = top->_right;
			}
		}
		cout << endl;
	}

(4) Sequence traversal:

void LevelOrder()
	{
		if (_root == NULL)
		{
			return;
		}
		queue<Node*> q;
		q.push(_root);
		while (!q.empty())
		{
			Node* front = q.front();
			cout << front->_data << " ";
			q.pop();
			if (front->_left != NULL)
			{
				q.push(front->_left);
			}
			if (front->_right != NULL)
			{
				q.push(front->_right);
			}
		}
		cout << endl;
	}

As for this sequence traversal, it is not the stack used, but the queue used. Each layer inserts one by one from left to right into the queue, then reads the data, and out of the queue, then goes to the left subtree or the right subtree, and then traverses to the next layer.

Implementation of all code and test function:

#include<iostream>
#include<assert.h>
#include<queue>
#include<stack>
using namespace std;

template<class T>
struct BinaryTreeNode
{
	T _data;
	BinaryTreeNode<T>* _left;
	BinaryTreeNode<T>* _right;

	BinaryTreeNode(const T& x)
		: _data(x)
		, _left(NULL)
		, _right(NULL)
	{}
};

template<class T>
class BinaryTree
{
	typedef BinaryTreeNode<T> Node;
public:
	BinaryTree(T* a, size_t size, const T& invalid = T())
	{
		assert(a);
		size_t index = 0;
		_root = _CreateTree(a, size, invalid, index);
	}

	BinaryTree(const BinaryTree<T>& t)
	{
		_root = _Copy(t._root);
	}


	BinaryTree<T>& operator=(BinaryTree<T> t)
	{
		std::swap(_root, t._root);
		return *this;
	}

	~BinaryTree()
	{
		_Destroy(_root);
	}

	void PrevOrder()
	{
		_PrevOrder(_root);
		cout << endl;
	}

	//Non-recursive implementation of preamble traversal
	void PrevOrderNonR()
	{
		stack<Node*> s;
		Node* cur = _root;

		while (!s.empty() || cur)
		{
			while (cur)
			{
				cout << cur->_data << " ";
				s.push(cur);
				cur = cur->_left;
			}

			Node* top = s.top();
			cur = top->_right;
			s.pop();
		}
		cout << endl;
	}

	void InOrder()
	{
		_InOrder(_root);
		cout << endl;
	}

	//Ordered traversal in non-recursive implementation
	void InOrderNonR()
	{
		stack<Node*> s;
		Node* cur = _root;
		while (cur || !s.empty())
		{
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}

			Node* top = s.top();
			cout << top->_data << " ";
			cur = top->_right;

			s.pop();
		}
		cout << endl;
	}

	void PostOrder()
	{
		_PostOrder(_root);
		cout << endl;
	}

	//Non-recursive post-order traversal
	void PostOrderNonR()
	{
		stack<Node*> s;
		Node* cur = _root;
		Node* prev = NULL;
		while (!s.empty() || cur)
		{
			while (cur)
			{
				s.push(cur);
				cur = cur->_left;
			}
			Node* top = s.top();
			if (top->_right==NULL || top->_right == prev)
			{
				cout << top->_data << " ";
				prev = top;
				s.pop();
			}
			else
			{
				cur = top->_right;
			}
		}
		cout << endl;
	}

	void LevelOrder()
	{
		if (_root == NULL)
		{
			return;
		}
		queue<Node*> q;
		q.push(_root);
		while (!q.empty())
		{
			Node* front = q.front();
			cout << front->_data << " ";
			q.pop();
			if (front->_left != NULL)
			{
				q.push(front->_left);
			}
			if (front->_right != NULL)
			{
				q.push(front->_right);
			}
		}
		cout << endl;
	}

	size_t Size()
	{
		return _Size(_root);
	}

	size_t Depth()
	{
		return _Depth(_root);
	}

	size_t GetLeafSize()
	{
		size_t count = 0;
		_GetLeafSize(_root, count);
		return count;
	}

	size_t GetKLevelSize(size_t k)
	{
		assert(k);
		return _GetKLevelSize(_root, k);
	}

protected:
	Node* _CreateTree(T* a, size_t size, const T& invalid, size_t& index)
	{
		if (index < size && a[index] != invalid)
		{
			Node* root = new Node(a[index]);
			root->_left = _CreateTree(a, size, invalid, ++index);
			root->_right = _CreateTree(a, size, invalid, ++index);
			return root;
		}
		return NULL;
	}

	void _Destroy(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		if (root->_left != NULL)
		{
			_Destroy(root->_left);
			root->_left = NULL;
		}
		if (root->_right != NULL)
		{
			_Destroy(root->_right);
			root->_right = NULL;
		}

		delete root;
		root = NULL;
		return;
	}

	Node* _Copy(Node* root)
	{
		if (root == NULL)
		{
			return NULL;
		}

		Node* NewNode = new Node(root->_data);
		NewNode->_left = _Copy(root->_left);
		NewNode->_right = _Copy(root->_right);

		return NewNode;
	}

	void _PrevOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		cout << root->_data << " ";
		_PrevOrder(root->_left);
		_PrevOrder(root->_right);
	}

	void _InOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		_InOrder(root->_left);
		cout << root->_data << " ";
		_InOrder(root->_right);
	}

	void _PostOrder(Node* root)
	{
		if (root == NULL)
		{
			return;
		}
		_PostOrder(root->_left);
		_PostOrder(root->_right);
		cout << root->_data << " ";
	}

	size_t _Size(Node* root)
	{
		if (root == NULL)
		{
			return 0;
		}
		return _Size(root->_left) + _Size(root->_right) + 1;
	}

	size_t _Depth(Node* root)
	{
		if (root == NULL)
		{
			return 0;
		}
		size_t left = _Depth(root->_left);
		size_t right = _Depth(root->_right);
		if (left < right)
		{
			return right + 1;
		}
		else
		{
			return left + 1;
		}
	}

	void _GetLeafSize(Node* root,size_t& count)
	{
		if (root->_left == NULL&&root->_right == NULL)
		{
			count++;
			return;
		}
		if (root->_left != NULL)
		{
			_GetLeafSize(root->_left, count);
		}
		if (root->_right != NULL)
		{
			_GetLeafSize(root->_right, count);
		}
	}

	size_t _GetKLevelSize(Node* root, size_t k)
	{
		if (root == NULL)
		{
			return 0;
		}
		if (k == 1)
		{
			return 1;
		}
		return _GetKLevelSize(root->_left, k - 1) + _GetKLevelSize(root->_right, k - 1);
	}

protected:
	Node* _root;
};

void TestBinaryTree()
{
	int a[10] = { 1, 2, 3, '#', '#', 4, '#', '#', 5, 6 };
	BinaryTree<int> t1(a, sizeof(a) / sizeof(a[0]), '#');
	
	cout << t1.Size() << endl;
	cout << t1.Depth() << endl;
	cout << t1.GetLeafSize() << endl;
	cout << t1.GetKLevelSize(3) << endl;
	t1.PrevOrder();
	t1.PrevOrderNonR();
	t1.InOrder();
	t1.InOrderNonR();
	t1.PostOrder();
	t1.PostOrderNonR();
	t1.LevelOrder();
}

Note: The code in this paper is implemented under VS2013 compiler.

Posted by mortal991 on Mon, 08 Apr 2019 15:09:32 -0700

Programmer Group

Recursive Implementation of Binary Tree

Recursive implementation of binary tree

Recursive Implementation of Binary Tree

Constructor:

(2) Copy constructor:

(3) Overload of assignment operators:

(4) Destructive function:

Recursive traversal of binary trees

(1) Preorder traversal:

(2) Mid-order traversal:

(3) Postorder traversal:

Non-recursive traversal of binary trees

(1) Preorder traversal:

(2) Mid-order traversal:

(3) Postorder traversal:

(4) Sequence traversal:

Implementation of all code and test function:

Hot Keywords