Preface

As long as we understand the idea, we can finish several lines of code. But non recursive writing is not easy. Here is a summary of their non recursive writing. Among them, the non recursive writing method of middle order traversal is the simplest, and the post order traversal is the most difficult.

Non recursive writing method of middle order traversal

The non recursive algorithm must use the stack (refer to the implementation of the stack in the complete code). Here I will focus on the writing method of middle order traversal.

void InorderTraversal(BinTree BT)
{
    BinTree T;
    Stack TreeStack;
    TreeStack = CreateStack();

    T = BT;
    while (T || !IsEmpty(TreeStack)){//Note the conditions at the end of the cycle
        while (T){   				//Put all the left subtree into the stack at one breath
            Push(TreeStack,T);		
            T = T->Left;			
        }
        T = Pop(TreeStack);			// When exiting the loop, T is empty, that is, there is no left subtree
        printf("%d  ", T->Data);	//At this point, print the node value
        T = T->Right;				//Then, turn to the right subtree, if the node is a leaf node,
        							//Then T is still empty, and the next cycle will directly output the stack,
        							//The code of leaf node and normal node is ingeniously unified here
    }
}

Non recursive writing method of post order traversal

Post order traversal needs to push the parent node into the stack twice and print the second time out of the stack, so it needs to be marked. The code is modified on the basis of the middle order traversal to understand the middle order traversal, and the following code is not difficult to understand.

void PostOrderTraversal(BinTree BT)
{
    BinTree T;
    Stack TreeStack;
    TreeStack = CreateStack();

    T = BT;
    while (T || !IsEmpty(TreeStack)){
        while (T){                          //Traverse left subtree
            Push(TreeStack,T);
            T = T->Left;
        }
        T = Pop(TreeStack);
        if (T->flag != 54321){              //54321 magic word, indicating that the right subtree has been stacked
            T->flag = 54321; 
            Push(TreeStack,T);              //Stack again and traverse the right subtree
            T = T->Right;
        } else {
            printf("%d  ", T->Data);
            T = NULL;                       //Clever use of NULL to lead right subtree in the next cycle
        }
    }
}

Complete code

/* Traversal of trees */
#include "stdio.h"
#include "stdbool.h"
#include <stdlib.h>

/* type define for Tree */
typedef struct TNode *Position;
typedef Position BinTree; /* Binary tree type */
struct TNode{           /* Tree node definition */
    int Data;           /* Node data */
    BinTree Left;       /* Point to left subtree */
    BinTree Right;      /* Point to right subtree */
    int flag;           /* For post order traversal, stack mark */
};

/* type define for stack */
typedef BinTree ElementType;
typedef struct SNode *PtrToSNode;
struct SNode {
    ElementType Data;
    PtrToSNode Next;
};
typedef PtrToSNode Stack;

Stack CreateStack( ) 
{ /* Build the header node of a stack and return the node pointer */
    Stack S;
 
    S = (Stack)malloc(sizeof(struct SNode));
    S->Next = NULL;
    return S;
}
 
bool IsEmpty ( Stack S )
{ /* Judge whether stack S is empty. If it is true, return false */
    return ( S->Next == NULL );
}
 
bool Push( Stack S, ElementType X )
{ /* Push element X onto stack S */
    PtrToSNode TmpCell;
 
    TmpCell = (PtrToSNode)malloc(sizeof(struct SNode));
    TmpCell->Data = X;
    TmpCell->Next = S->Next;
    S->Next = TmpCell;
    return true;
}
 
ElementType Pop( Stack S )  
{ /* Delete and return stack top element of stack S */
    PtrToSNode FirstCell;
    ElementType TopElem;
 
    if( IsEmpty(S) ) {
        printf("Stack empty"); 
        return NULL;
    }
    else {
        FirstCell = S->Next; 
        TopElem = FirstCell->Data;
        S->Next = FirstCell->Next;
        free(FirstCell);
        return TopElem;
    }
}

BinTree TreeCreat()    //Build the tree to be verified
{
    BinTree T,BT;
    BT = (BinTree)malloc(sizeof(struct TNode));
    /* A */
    T = BT;             
    T->Data = 1;
    T->Left = (BinTree)malloc(sizeof(struct TNode));
    T->Right = (BinTree)malloc(sizeof(struct TNode));
    /* B */
    T = BT->Left;       
    T->Data = 2;        
    T->Left = (BinTree)malloc(sizeof(struct TNode));
    T->Right = (BinTree)malloc(sizeof(struct TNode));
    /* C */
    T = BT->Right;      
    T->Data = 3;
    T->Left = (BinTree)malloc(sizeof(struct TNode));
    T->Right = (BinTree)malloc(sizeof(struct TNode));
    /* D */
    T = BT->Left->Left; 
    T->Data = 4;
    T->Left = NULL;
    T->Right = NULL;
    /* E */
    T = BT->Left->Right; 
    T->Data = 5;
    T->Left = (BinTree)malloc(sizeof(struct TNode));
    T->Right = NULL;
    /* F */
    T = BT->Right->Left; 
    T->Data = 6;
    T->Left = NULL;
    T->Right = (BinTree)malloc(sizeof(struct TNode)); 
    /* G */
    T = BT->Right->Right; 
    T->Data = 7;
    T->Left = NULL;
    T->Right = NULL;
    /* H */
    T = BT->Left->Right->Left; 
    T->Data = 8;
    T->Left = NULL;
    T->Right = NULL;    
    /* I */
    T = BT->Right->Left->Right; 
    T->Data = 9;
    T->Left = NULL;
    T->Right = NULL;

    return BT;
}
void InorderTraversal(BinTree BT)
{
    BinTree T;
    Stack TreeStack;
    TreeStack = CreateStack();

    T = BT;
    while (T || !IsEmpty(TreeStack)){
        while (T){
            Push(TreeStack,T);
            T = T->Left;
        }
        T = Pop(TreeStack);
        printf("%d  ", T->Data);
        T = T->Right;
    }

}
void PreOrderTraversal(BinTree BT)
{
    BinTree T;
    Stack TreeStack;
    TreeStack = CreateStack();

    T = BT;
    while (T || !IsEmpty(TreeStack)){
        while (T){
            printf("%d  ", T->Data);
            Push(TreeStack,T);
            T = T->Left;
        }

        T = Pop(TreeStack);
        T = T->Right;
    }

}

void PostOrderTraversal(BinTree BT)
{
    BinTree T;
    Stack TreeStack;
    TreeStack = CreateStack();

    T = BT;
    while (T || !IsEmpty(TreeStack)){
        while (T){                          //Traverse left subtree
            Push(TreeStack,T);
            T = T->Left;
        }
        T = Pop(TreeStack);
        if (T->flag != 54321){              //54321 magic word, indicating that the right subtree has been stacked
            T->flag = 54321; 
            Push(TreeStack,T);              //Stack again and traverse the right subtree
            T = T->Right;
        } else {
            printf("%d  ", T->Data);
            T = NULL;                       //Clever use of NULL to lead right subtree in the next cycle
        }
    }
}

void PreOrderTraversal_R(BinTree BT)
{
    if(BT){
        printf("%d  ", BT->Data);
        PreOrderTraversal(BT->Left);
        PreOrderTraversal(BT->Right);
    }
}
void InOrderTraversal_R(BinTree BT)
{
    if(BT){
        InOrderTraversal_R(BT->Left);
        printf("%d  ", BT->Data);
        InOrderTraversal_R(BT->Right);
    }
}
void PostOrderTraversal_R(BinTree BT)
{
    if(BT){
        PostOrderTraversal_R(BT->Left);
        PostOrderTraversal_R(BT->Right);
        printf("%d  ", BT->Data);
    }
}
int main()
{
    BinTree BT = TreeCreat();
    printf("PostOrderTraversal_R:");
    PostOrderTraversal_R(BT);
    printf("\r\n");
    printf("PostOrderTraversal_L:");
    PostOrderTraversal(BT);
    printf("\r\n");
    return 0;
}

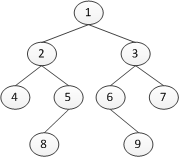
The structure of the tree constructed in the code