Recursive and Divide-and-conquer Strategy
1. Recursion
1. Distinguish Recursion from Cycle
Recursive: You open the door in front of you and see that there is still a door in the house. You walk over and find that the key in your hand can open it. You push open the door and find that there is still a door in it. You continue to open it. A few times later, when you open the door in front of you, you find that there is only one room with no door. Then you start to go back the same way and you count once for every room you walk back.When you get to the entrance, you can answer how many doors you have opened with your key.
Circulation: When you open the door in front of you, you see that there is still a door in the house. When you walk over, you find that the key in your hand can still open it. When you open the door, you find that there is still a door inside.(If the front two doors are the same, so is the door and the front two; if the second door is smaller than the first, then the door is smaller than the second one. You keep opening the door and keep going like this until you open all the doors. However, the person at the entrance can't wait for you to go back and tell him the answer.
2. Partial Treatment
1. Basic Ideas
The design idea of divide-and-conquer is to divide a big problem that is difficult to solve directly into smaller, identical problems so that each can be broken and conquered separately.
The divide-and-conquer strategy is that if a problem of scale n can be easily solved (e.g., smaller scale n)Then solve them directly, or decompose them into k smaller subproblems, which are independent of each other and have the same form as the original problem, solve them recursively, and merge the solutions of each subproblem to get the solution of the original problem. This algorithm design strategy is called divide and conquer.
If the original problem can be divided into k sub-problems, 1 < K < n, and these sub-problems can be solved and the solution of the original problem can be found by using the solutions of these sub-problems, this kind of division and conquer method is feasible. The sub-problems caused by division and conquer method are often smaller patterns of the original problem, which provides convenience for using recursive technology. In this case, repeated application of division and conquer method can make sub-problems easier to use.The problem is identical to the original problem type but its size is shrinking, which ultimately reduces the subproblem to an easy direct solution. This naturally leads to a recursive process. Divide and recursion, like twin brothers, are often used together in algorithm design, resulting in many efficient algorithms.
2. Application
The problem that divide and conquer can solve generally has the following characteristics:
1) This problem can be easily solved by reducing its size to a certain extent 2) The problem can be decomposed into several smaller, identical problems that have optimal substructural properties. 3) The solution of the subproblem decomposed by the problem can be merged into the solution of the problem. 4) The subproblems resolved by this problem are independent, that is, they do not contain common subproblems.
The first feature is that most problems can be satisfied, because the computational complexity of a problem generally increases with the size of the problem.
The second feature is that the precondition for applying divide-and-conquer is that most problems can be satisfied, and this feature reflects the application of recursive thinking;
The third feature is the key. Whether or not the divide-and-conquer method can be used depends entirely on whether the problem has the third feature. If it has the first and second features but not the third one, greed or dynamic planning can be considered.
The fourth feature relates to the efficiency of the divide-and-conquer method. If the sub-problems are not independent, the divide-and-conquer method will do a lot of unnecessary work, and solve the common sub-problems repeatedly. At this time, although the divide-and-conquer method can be used, the dynamic planning method is generally better.
2. Basic steps
Divide and conquer has three steps in each level of recursion:
step1 Decomposition: Decomposition the original problem into several smaller, independent, and identical subproblems. step2 Solve: If the sub-problem is small and easy to solve, solve it directly, otherwise solve each sub-problem recursively step3 Merge: Combine the solutions of each subproblem into the solution of the original problem.
Its general algorithm design pattern is as follows:
Divide-and-Conquer(P) 1. if |P|≤n0 2. then return(ADHOC(P)) 3. take P Decomposition into smaller subproblems P1 ,P2 ,...,Pk 4. for i←1 to k 5. do yi ← Divide-and-Conquer(Pi) △ Recursive Solution Pi 6. T ← MERGE(y1,y2,...,yk) △ Merge Subproblems 7. return(T) among|P|Represent the problem P Size; n0 Is a threshold value indicating when the problem occurs P Size not exceeding n0 When the problem is solved directly, it is not necessary to decompose it any more. ADHOC(P)Is the basic subalgorithm of this division and conquer method, used to solve small-scale problems directly P. So when P Size not exceeding n0 Use algorithm directly ADHOC(P)Solve. Algorithms MERGE(y1,y2,...,yk)Is the merge subalgorithm of the division and conquer method used to P Subproblems P1 ,P2 ,...,Pk Corresponding solution y1,y2,...,yk Merge into P Solution.
3. Solving methods of recursive equations
1. Iteration
Continuously replace the left part with the right part of the recursive equation. The following is an example of Hannotta solving.
Insert a picture description here

Sometimes direct iteration may be inconvenient, so meta-iteration can be used. The following is an example of a binary regression and sorting iteration equation.
Insert a picture description here

2. Differential elimination
Differential elimination is generally used on the right side of a recursive equation not only depending on the previous term of the current term, but also on the first many terms. This recursive equation is cumbersome to iterate directly. It belongs to a higher-order recursive equation, so it is necessary to subtract the higher-order recursive equation before iterating. Take a quick-sorted recursive equation as an example.
Insert a picture description here

3. Recursive Tree
Establish a recursive tree with each iteration using the function item as the son and the non-function item as the root value. Take the binary recursion and sorting recursive equation as an example.
Insert a picture description here

4. Principal Theorem
Insert a picture description here

Here is an example:

4. Algorithmic Complexity Analysis
A divide-and-conquer method divides a problem of scale n into k sub-problems of scale n/m to solve. Setting the decomposition threshold n0=1 takes 1 unit time for an adhoc problem of scale 1. Setting the original problem into k sub-problems and merge the solutions of K sub-problems into original problems takes f(n) units time.The computation time required to solve a problem of scale |P|=n is indicated by:
T(n)= k T(n/m)+f(n)
3. Sorting problems
1. Merge Sort
1. Concepts
Merge Sort is an efficient, universal, comparison-based divide and conquer sorting algorithm. Most implementations produce a stable sort, meaning that the input order of the desired elements in the sort output is preserved. Merge Sort is a divide and conquer algorithm, invented by Von Neumann in 1945.
2. Basic Ideas
Divides the elements to be sorted into two identical subsets of approximately the same size, sorting the two subsets separately, and finally merges the ordered subsets into the required ordered set.
Input: An input array A consisting of a series of unordered elements (eg. numbers).
After: two steps. The first step is to recursively divide the whole problem into a subproblem/subarray containing only one element (eg, the initial problem is {2,1,5,6,4,10}, divided directly into 2,1,5,6,4,10)
The second step, step by step, combines the decomposed subarrays into an ordered array, comparing each self-array (only one element) in pairs and combining them into a subarray (two elements) in size order.again
Two pairs of subarrays now merge into a new one in size order... and so on, until the last two subarrays are compared and the elements are merged into the final ordered sequence in size order.
Output: Output array B, which contains elements from A but has been ordered as required.
When the number of array elements is odd:

When the number of array elements is even:
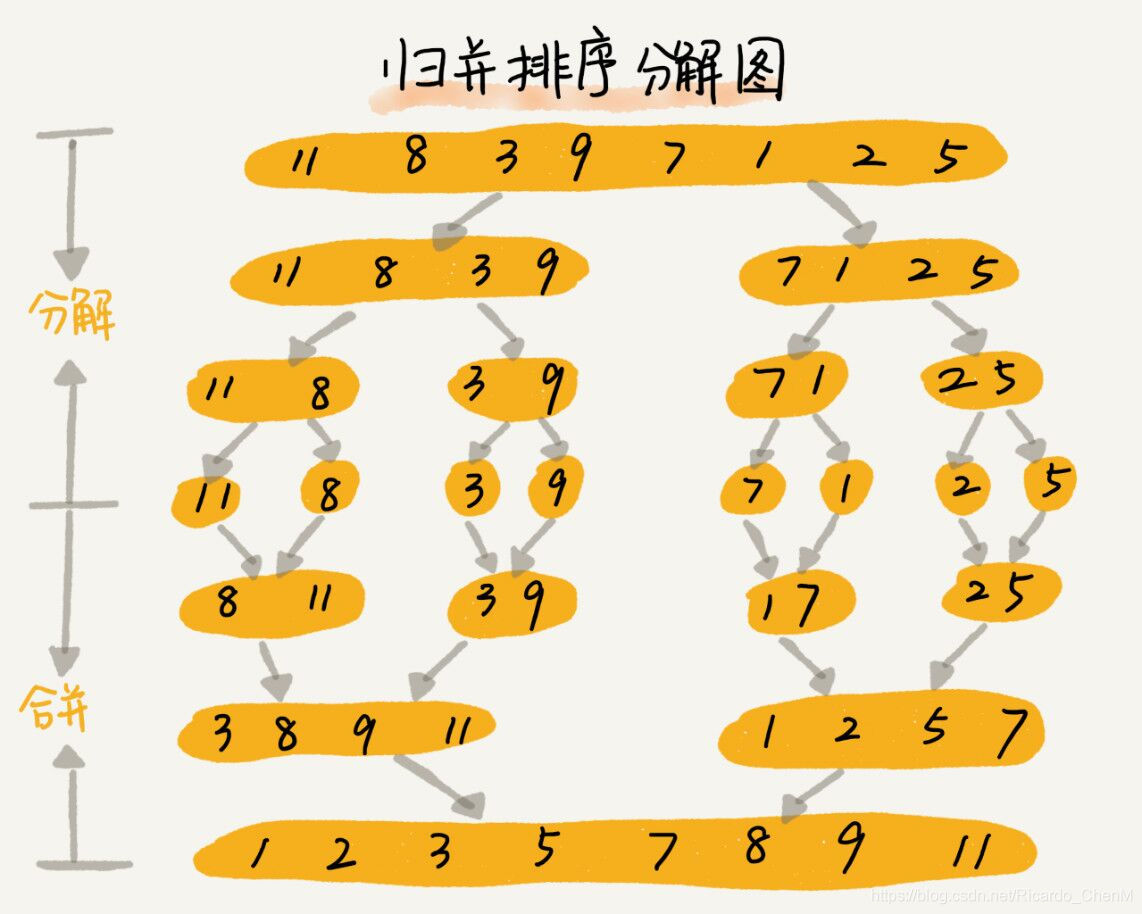
3. Working principle
3.1. Workflow
1. Divide the unsorted list into n sublists, each containing an element (a list of elements is considered sorted).
2. Combine sublists repeatedly to produce a new sorted sublist until only one is left.
3.2. Mode of division
top-down
The top-down implementation uses the principle of recursion. It starts at the top of the book and then goes down, asking the same question each time (what do I need to do to sort this array?) and answering it (dividing it into two subarrays, making recursive calls, merging the results) until we reach the bottom of the tree.
From bottom to top
Bottom-up implementations do not need to be recursive. They start directly at the bottom of the tree and then merge the fragments by traversing them.
In fact, any merge sort can be visualized as a tree operation. The leaves in the tree represent the elements in the array. Each internal node of the tree corresponds to combining two smaller numbers into a larger array.
4. Code implementation
Recursive Version
#include<bits/stdc++.h>
#define Maxn 10001
using namespace std;
void Merge(int arr[], int l, int mid, int r);
void MergeSort(int arr[], int l, int r);
void displayArray(int arr[], int n);
int main()
{
int arr[Maxn];
cout << "Please enter the number of array elements: " << endl;
int n;
cin >> n;
cout << "Please" << n << "Enter an array element in line" << endl;
for(int i = 0; i < n; i++)
cin >> arr[i];
cout << "The initial state of the array is: " << endl;
displayArray(arr, n);
MergeSort(arr, 0, n-1);
cout << "The merged and sorted state of the array is: " << endl;
displayArray(arr, n);
}
void Merge(int arr[], int l, int mid, int r)
{
int i, j, k;
int n1 = mid - l + 1; //Length of left half
int n2 = r - mid; //Length of right half
int *L = new int[n1+1]; //Open up temporary space
int *R = new int[n2+1];
for(i = 0; i < n1; i++)
L[i] = arr[i+l]; //Subscript fills in elements of array a starting at 0
for(j = 0; j < n2; j++)
R[j] = arr[j+mid+1];
L[n1] = INT_MAX;
R[n2] = INT_MAX;
i = 0;
j = 0;
for(k = l; k <= r; k++) //merge
{
if(L[i] <= R[j])
//Notice here that the value of L[i] is assigned to a[k], then i+.
//This is for ease of operation
//The following else statement is the same
arr[k] = L[i++];
else
arr[k] = R[j++];
}
}
void MergeSort(int arr[], int l, int r) //p->left r->right
{
if(l < r)
{
int mid = (l + r) / 2; //q is the midpoint
MergeSort(arr, l, mid); //Complete sort on left half
MergeSort(arr, mid+1, r); //Complete sort on right half
Merge(arr, l, mid, r); //Combines a sorted array of halves into an array sort
}
}
void displayArray(int arr[], int n)
{
for(int i = 0; i < n-1; i++)
cout << arr[i] << " ";
cout << arr[n-1] << endl;
}
Non-recursive version (later available)
5. Algorithmic Analysis
Classification: Sorting algorithm
Algorithms: Divide and conquer algorithm
Data structure: array
Optimal time complexity: O(nlog(n))
Worst-case time complexity: O(nlog(n))
Average time complexity: O(nlog(n))
Worst-case spatial complexity: total O(n), auxiliary O(n); when linked list is used, auxiliary space is O(1)
Stability: Stability
Complexity: More complex