Recursion in JavaScript

Translator's Note: Programmers should know recursion, but do you really know what's going on?

Original: All About Recursion, PTC, TCO and STC in JavaScript

Translator: Fundebug

In order to ensure readability, free translation is adopted instead of literal translation.

A Brief Introduction to Recursion

> A process or function has a method to call itself directly or indirectly in its definition or description. It usually transforms a large and complex problem layer by layer into a smaller problem similar to the original problem to solve. The recursive strategy only needs a small number of programs to describe the repeated calculation needed in the process of solving the problem, which greatly reduces the amount of code in the program.

Let's take an example. We can use the factorial of 4 to define the factorial of 5, the factorial of 3 to define the factorial of 4, and so on.

factorial(5) = factorial(4) * 5
factorial(5) = factorial(3) * 4 * 5
factorial(5) = factorial(2) * 3 * 4 * 5
factorial(5) = factorial(1) * 2 * 3 * 4 * 5
factorial(5) = factorial(0) * 1 * 2 * 3 * 4 * 5
factorial(5) = 1 * 1 * 2 * 3 * 4 * 5

With Haskell's Patternmatching, factorial functions can be defined intuitively:

factorial n = factorial (n-1)  * n
factorial 0 = 1

In the recursive example, starting with the first call to factorial(5), the factorial function itself is called recursively until the value of the parameter is 0. Here is an image of the following:

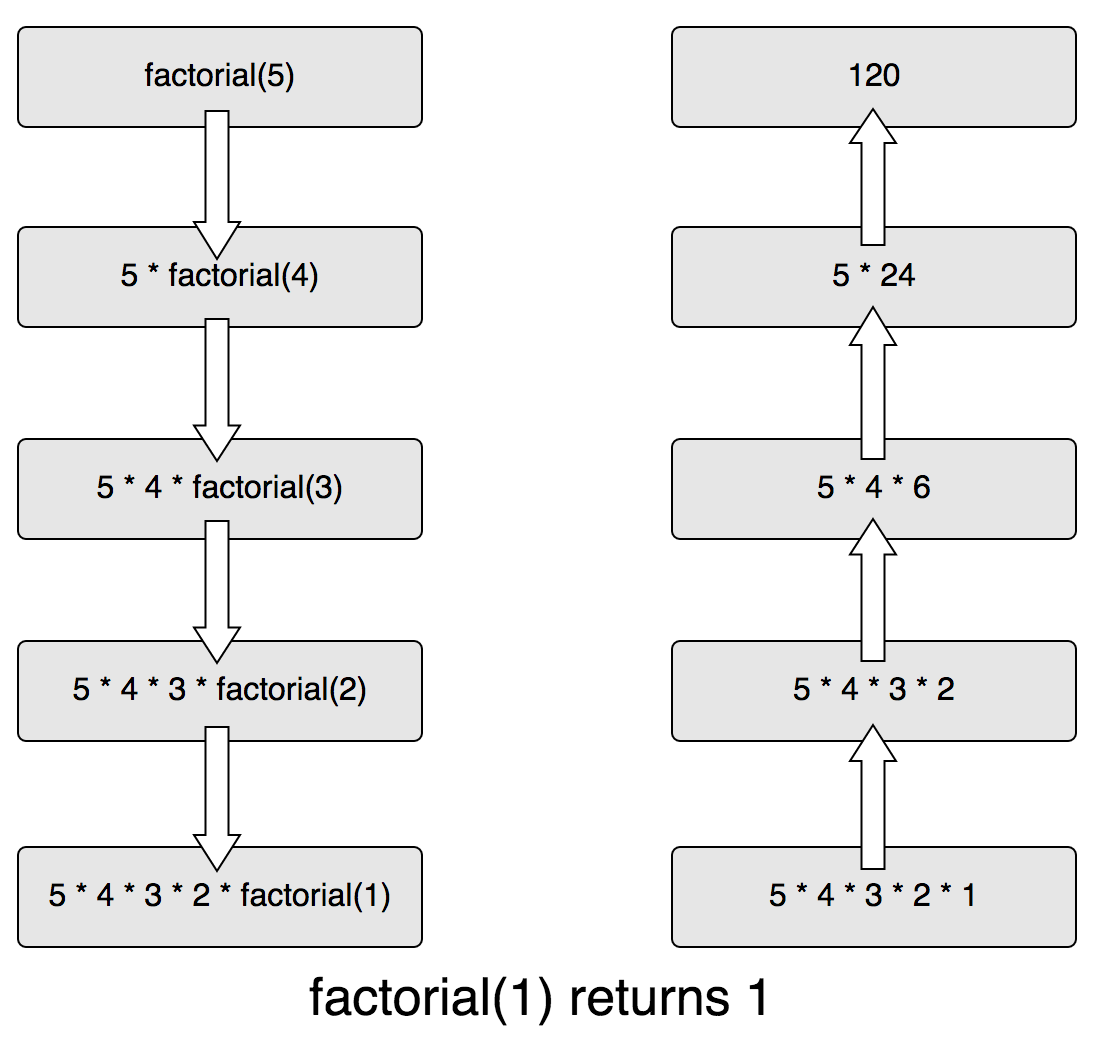
Recursive call stack

To understand the call stack, let's go back to the factorial function example.

function factorial(n) {
    if (n === 0) {
        return 1
    }

    return n * factorial(n - 1)
}

If we pass in parameter 3, factorial(2), factorial(1) and factorial(0) will be called recursively, so factorial will be called three more times.

Each function call is pushed into the call stack. The whole call stack is as follows:

factorial(0) // The factorial of 0 is 1. 
factorial(1) // The call depends on factorial(0)
factorial(2) // The call depends on factorial(1)
factorial(3) // The switch depends on factorial(2)

Now let's modify the code and insert console.trace() to see the status of each current call stack:

function factorial(n) {
    console.trace()
    if (n === 0) {
        return 1
    }

    return n * factorial(n - 1)
}

factorial(3)

Next, let's look at the call stack. First:

Trace
    at factorial (repl:2:9)
    at repl:1:1 // Ignore the following underlying implementation details
    at realRunInThisContextScript (vm.js:22:35)
    at sigintHandlersWrap (vm.js:98:12)
    at ContextifyScript.Script.runInThisContext (vm.js:24:12)
    at REPLServer.defaultEval (repl.js:313:29)
    at bound (domain.js:280:14)
    at REPLServer.runBound [as eval] (domain.js:293:12)
    at REPLServer.onLine (repl.js:513:10)
    at emitOne (events.js:101:20)

You will find that the call stack contains a call to the factorial function, which is factorial(3). Next, more interesting, let's look at the second printed call stack:

Trace
    at factorial (repl:2:9)
    at factorial (repl:7:12)
    at repl:1:1 // Ignore the following underlying implementation details
    at realRunInThisContextScript (vm.js:22:35)
    at sigintHandlersWrap (vm.js:98:12)
    at ContextifyScript.Script.runInThisContext (vm.js:24:12)
    at REPLServer.defaultEval (repl.js:313:29)
    at bound (domain.js:280:14)
    at REPLServer.runBound [as eval] (domain.js:293:12)
    at REPLServer.onLine (repl.js:513:10)

Now we have two calls to factorial functions.

Third time:

Trace
    at factorial (repl:2:9)
    at factorial (repl:7:12)
    at factorial (repl:7:12)
    at repl:1:1
    at realRunInThisContextScript (vm.js:22:35)
    at sigintHandlersWrap (vm.js:98:12)
    at ContextifyScript.Script.runInThisContext (vm.js:24:12)
    at REPLServer.defaultEval (repl.js:313:29)
    at bound (domain.js:280:14)
    at REPLServer.runBound [as eval] (domain.js:293:12)

Fourth time:

Trace
    at factorial (repl:2:9)
    at factorial (repl:7:12)
    at factorial (repl:7:12)
    at factorial (repl:7:12)
    at repl:1:1
    at realRunInThisContextScript (vm.js:22:35)
    at sigintHandlersWrap (vm.js:98:12)
    at ContextifyScript.Script.runInThisContext (vm.js:24:12)
    at REPLServer.defaultEval (repl.js:313:29)
    at bound (domain.js:280:14)

Imagine that if the value of the parameter passed in is particularly large, the call stack will be very large and may eventually crash beyond the cache size of the call stack, causing the program to fail to execute. So how to solve this problem? Use tail recursion.

Tail recursion

Tail recursion is a recursive way of writing, which can avoid the stack overflow caused by constantly stacking functions. By setting a cumulative parameter and adding the current value each time, it is called recursively.

Let's see how to rewrite the previous definition of factorial function as tail recursion:

function factorial(n, total = 1) {
    if (n === 0) {
        return total
    }

    return factorial(n - 1, n * total)
}

The implementation steps of factorial(3) are as follows:

factorial(3, 1) 
factorial(2, 3) 
factorial(1, 6) 
factorial(0, 6)

The call stack no longer needs to stack factorial multiple times, because each recursive call does not depend on the value of the previous recursive call. Therefore, the complexity of space is o(1) instead of 0(n).

Next, the call stack is printed out through the console.trace() function.

function factorial(n, total = 1) {
    console.trace()
    if (n === 0) {
        return total
    }

    return factorial(n - 1, n * total)
}

factorial(3)

Surprisingly, there are still many stacks!

// ...
// Here are the last two calls to factorial
Trace
    at factorial (repl:2:9) // 3 times stack
    at factorial (repl:7:8)
    at factorial (repl:7:8)
    at repl:1:1 // Ignore the following underlying implementation details
    at realRunInThisContextScript (vm.js:22:35)
    at sigintHandlersWrap (vm.js:98:12)
    at ContextifyScript.Script.runInThisContext (vm.js:24:12)
    at REPLServer.defaultEval (repl.js:313:29)
    at bound (domain.js:280:14)
    at REPLServer.runBound [as eval] (domain.js:293:12)
Trace
    at factorial (repl:2:9) // Finally, the first call pushes the stack again
    at factorial (repl:7:8)
    at factorial (repl:7:8)
    at factorial (repl:7:8)
    at repl:1:1 // Ignore the following underlying implementation details
    at realRunInThisContextScript (vm.js:22:35)
    at sigintHandlersWrap (vm.js:98:12)
    at ContextifyScript.Script.runInThisContext (vm.js:24:12)
    at REPLServer.defaultEval (repl.js:313:29)
    at bound (domain.js:280:14)

Why is that? Under Nodejs, we can turn on proper tail call by opening strict mode and using -- harmony_tailcalls.

'use strict'

function factorial(n, total = 1) {
    console.trace()
    if (n === 0) {
        return total
    }

    return factorial(n - 1, n * total)
}

factorial(3)

Use the following commands:

node --harmony_tailcalls factorial.js

The call stack information is as follows:

Trace
    at factorial (/Users/stefanzan/factorial.js:3:13)
    at Object.<anonymous> (/Users/stefanzan/factorial.js:9:1)
    at Module._compile (module.js:570:32)
    at Object.Module._extensions..js (module.js:579:10)
    at Module.load (module.js:487:32)
    at tryModuleLoad (module.js:446:12)
    at Function.Module._load (module.js:438:3)
    at Module.runMain (module.js:604:10)
    at run (bootstrap_node.js:394:7)
    at startup (bootstrap_node.js:149:9)
Trace
    at factorial (/Users/stefanzan/factorial.js:3:13)
    at Object.<anonymous> (/Users/stefanzan/factorial.js:9:1)
    at Module._compile (module.js:570:32)
    at Object.Module._extensions..js (module.js:579:10)
    at Module.load (module.js:487:32)
    at tryModuleLoad (module.js:446:12)
    at Function.Module._load (module.js:438:3)
    at Module.runMain (module.js:604:10)
    at run (bootstrap_node.js:394:7)
    at startup (bootstrap_node.js:149:9)
Trace
    at factorial (/Users/stefanzan/factorial.js:3:13)
    at Object.<anonymous> (/Users/stefanzan/factorial.js:9:1)
    at Module._compile (module.js:570:32)
    at Object.Module._extensions..js (module.js:579:10)
    at Module.load (module.js:487:32)
    at tryModuleLoad (module.js:446:12)
    at Function.Module._load (module.js:438:3)
    at Module.runMain (module.js:604:10)
    at run (bootstrap_node.js:394:7)
    at startup (bootstrap_node.js:149:9)
Trace
    at factorial (/Users/stefanzan/factorial.js:3:13)
    at Object.<anonymous> (/Users/stefanzan/factorial.js:9:1)
    at Module._compile (module.js:570:32)
    at Object.Module._extensions..js (module.js:579:10)
    at Module.load (module.js:487:32)
    at tryModuleLoad (module.js:446:12)
    at Function.Module._load (module.js:438:3)
    at Module.runMain (module.js:604:10)
    at run (bootstrap_node.js:394:7)
    at startup (bootstrap_node.js:149:9)

You'll find that you don't stack every call, there's only one factorial.

Note: Tail recursion does not necessarily increase the speed of your code execution; on the contrary, tail recursion does not necessarily increase the speed of your code execution. It may slow down. . However, tail recursion allows you to use less memory and make your recursive functions safer (provided you turn on harmony mode).

So the blogger wonders: Why does tail normalization have to turn on harmony mode? Welcome to join the discussion.

Welcome to join us We Fundebug Full stack BUG monitoring communication group: 622902485.

Copyright Statement: When reproducing, please indicate the author Fundebug and the address of this article: https://blog.fundebug.com/2017/06/14/all-about-recursions/

Did your users encounter BUG?

Experience Demo Free use

Posted by gum1982 on Thu, 20 Jun 2019 15:54:00 -0700

Programmer Group

Recursion in JavaScript

A Brief Introduction to Recursion

Recursive call stack

Tail recursion

Hot Keywords